74 75 3.3. Распределение вектора выборочного среднего; заключение о среднем значении, когда ковариационная матрица известна

3.3.1. Теория распределения. В одномерном случае вы­борочное среднее распределено нормально и не зависит от выборочной дисперсии. Аналогично выборочное среднее , определенное в § 3.2, распределено нормально и не зави­сит от .

Чтобы доказать этот результат, мы произведем преобра­зование множества векторов наблюдений. В связи с тем, что этот вид преобразований применяется неоднократно в этой книге, сначала докажем более общую теорему.

Теорема 3.3.1. Допустим, что X₁ ..., X_N неза­висимы, причем распределен. ПустьС=-ортогональная матрица. Тогда распределенN(,), гдеи независимы.

Доказательство. Совместное распределение множе­ства векторов {} нормально, так как все множество компо­нент является множеством линейных комбинаций компо­нент{Х},совместное распределение которых нормально. Математическое ожидание , равно

(1)

Ковариационная матрица векторов и равна

(2)

где есть символ Кронекера (= 1 прии=0 при). Отсюда видно, что не зависит от и имеет ковариационную матрицу .

Применим также следующую общую лемму.

Лемма 3.3.1. Если С= ортогональна, то =, где

Доказательство.

(3)

Пусть независимы и одинаково распределены с законом распределения

N(). Существует ортогональная матрицаВ = ()порядка последняя строка кото­рой будет

. (4)

Это преобразование можно представить в виде поворота в N-мерном пространстве, при котором прямая, образующая равные углы с осями координат, переходит в N-ю ось коор­динат (см. § 3.2). Пусть A=N^, где определена в § 3.2, и пусть

.(5)

Тогда

. (6)

Согласно лемме 3.3.1,

(7)

Так как не зависит от, то не зависит от А. Так как

, (8)

то Z_N распределен иZ_N распре­делен . Заметим, что

, (9)

Теорема З.З.2. Среднее значение выборки объема N из генеральной совокупности распределено N не зависит от , являющейся оценкой наибольшего правдоподобия для . N распределена как , где , pacnpeдeлeн N (0,) и не зависит от.

Заметим, что

(10)

Таким образом, является смещенной оценкой. Поэтому мы определим

(11)

как выборочную ковариационную матрицу. Она является несмещенной оценкой , и ее диагональные элементы являются обычными (несмещенными) выборочными дисперсиями компонентX.

3.3.2. Критерии и доверительные области для , когдаизвестна. Важными статистическими проблемами являются проблема проверки гипотезы о том, что вектор среднего зна­чения нормального распределения является данным вектором, и связанная с ней проблема определения доверительной области для неизвестного вектора среднего значения. Мы рассмотрим здесь эти проблемы в предположении, что ковариационная матрица известна. В главе 5 мы рассмотрим случай, когда ковариационная матрица неизвестна.

Для одномерного случая основой для выбора критерия, или доверительного интервала служит тот факт, что разность между средними значениями выборки и генеральной совокупности распределена нормально с математическим ожиданием, равным нулю, и известной дисперсией; тогда таблицы нормального распределения могут быть использованы для точечных оценок или вычисления доверительных интервалов. В многомерном случае будет использован тот факт, что раз­ность между векторами среднего значения выборки и сред­него значения генеральной совокупности распределена нор­мально с вектором среднего значения, равным нулю, и известной ковариационной матрицей. Можно установить пре­делы для каждой компоненты на основании распределения, но неудобства такой процедуры состоят в том, что сам выбор пределов является отчасти произвольным и дает кри­терии, довольно бедные в некотором отношении; больше того, такие пределы трудно вычислять, так как таблицы пригодны только для двумерного случая. Методы, приведен­ные ниже, дают возможность простых вычислений и к тому же могут быть подвергнуты общей интуитивной теоретической проверке.

Эти методы основываются на следующей теореме.

Теорема 3.3.3. Если т-мерный вектор Y распре­делен N(0,T) (невырожденное распределение), то имеетраспределение с т степенями свободы.

Доказательство. Пусть С— невырожденная матрица, такая, что СТС' = I, и положим

Z = CY. Тогда Z нормально распределен со средним значением MZ = CMY = 0 и кова­риационной матрицей

MZZ' = МСYY'C' = СТС' == I.

Но

,

что является суммой квадратов компонент Z. Так как компо­ненты Z независимы и распределены N (0, 1), то Z'Z= Y' T^-1Y имеет -распределение сm степенями свободы (см. задачу 5 главы 7).

Так как распределенN(0,), то из тео­ремы следует, что

(12)

имеет -распределение ср степенями свободы. Это важное положение мы применим при выборе критериев и довери­тельных областей для .

79

Пусть — такое число, что

(13)

.

Тогда

(14)

Для проверки гипотезы о том, что , где— опре­деленный вектор, мы используем в качестве критической области

(15)

.

Если мы получим выборку, удовлетворяющую (15), то нуле­вая гипотеза отвергается. Интуитивно ясно, что вероятность отбросить гипотезу больше , если значительно отличается от , так как в пространстве (15) определяет эллипс с центром в , и еслиотстоит далеко от, то плотность вероятности сосредоточена в точке у границы или вне эллипса. Доказательство теоремы 3.3.3 может быть расши­рено, чтобы показать, что имеет нецентральное-распределение ср степенями свободы и параметром , когдаX есть среднее значение выборки объема N из совокупности N () (дано Р. Бозе [1], [2]). Теорему 3.3.3 первым доказал К. Пирсон [2].

Теперь рассмотрим следующее утверждение, сделанное на основе выборки со средним значением : «Среднее зна­чение распределения удовлетворяет условию

(16)

как неравенству относительно ». Из (14) видно, что вероят­ность получения выборки, для которой указанное утвержде­ние правильно, равна 1—, так как событие в (14) экви­валентно тому, что это утверждение ложно. Таким образом, множество*, удовлетворяющих (16), является определением доверительной области дляс доверительным уровнем 1 —. В р-мерном пространстве (15) является поверхностью и внешней частью эллипсоида с центром в , форма эллип­соида зависит от, а объем — от (1/N)при данном. В p-мерном пространстве * (16) является поверх­ностью и внутренней частью эллипсоида с центром в. Если то (14) говорит, чтоесть вероятность того, что расстояние между и больше, чем

Теорема 3.3.4. Если —среднее значение выборки объемаN, взятой из совокупности N (), и из­вестна, то (15) определяет критическую область вероят­ности для проверки гипотезы и (16) дает до­верительную область для с доверительным уровнем 1 —.выбирается так, чтобы удовлетворить (13).

Такая же техника может быть использована для соответ­ствующих проблем в случае двух выборок. Предположим, что у нас имеется выборка () из сово­купности, распределенной, и выборка()из другой нормальной совокупностис той же ковариационной матрицей. Тогда оба выборочных средних

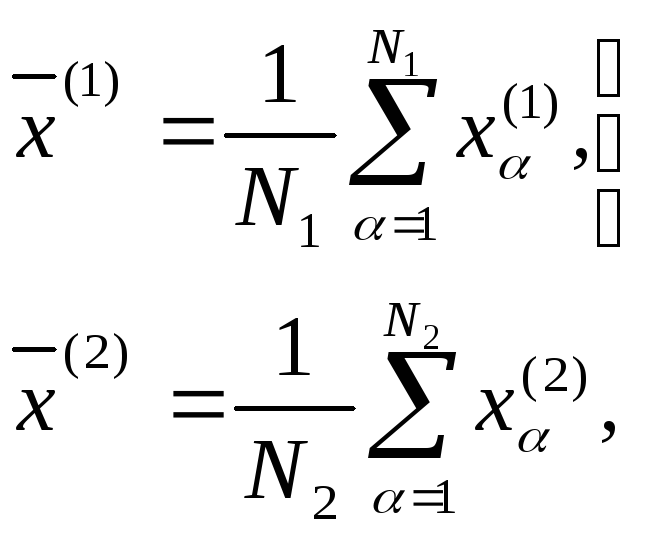(17)

независимы и распределены иN [] соответственно. Разность двух выборочных средниху =распределена , где. Таким образом,

(18)

является доверительной областью для разности двух век­торов средних значений, а критическая область для про­верки гипотезыдана неравенством

. (19)

81

Махаланобис [1] предложил рассматривать

как меру расстояния между двумя совокупностями.

3.3.3. Достаточные статистики для и.Было по­казано, что

. (20)

(21)

Таким образом, совместная плотность может быть записана следующим образом:

(22)

Таким образом, и (1/N)A образуют достаточные стати­стики для , и. Еслиизвестна, то: является достаточ­ной статистикой для. Однако если известен, то(1/N)A не является достаточной статистикой для , но

является достаточной статистикой для . Напомним, чтоt является достаточной статистикой для , если

(23)

где есть плотность вероятности для-го наблюде­ния;g(t;) — плотность распределения t и h(x₁, ..., х_n) не зависит от 6 (Крамер [2]).

Если среднее значение q-мерного случайного вектора Y равно МY=и его ковариационная матрица равнаM(Y— )(Y— )' =, то

(24)

называется эллипсоидом рассеяния для Y (см. Крамер [2]). Плотность вероятности, определяемая равномерным распре­делением в внутренней части этого эллипсоида, имеет тот же вектор среднего значения и ту же ковариационную матрицу, что и Y (см. задачу 44 главы 2). Пусть — вектор, состоя­щий изq параметров распределения, и пусть t—вектор не­смещенных оценок (т. е. Mt=), полученный поN наблю­дениям над этим распределением с ковариационной матрицей . Тогда эллипсоид

(25)

целиком лежит внутри эллипсоида рассеяния t; обозначает вектор-столбец производных плотности веро­ятности (или вероятностной функции) по компонентам . В работе Крамера [2] рассуждение проводится для скаляра наблюдений, но ясно, что оно справедливо и для вектора наблюдений. Если (25) есть эллипсоид рассеяния дляt, то t на­зывается эффективным. В общем случае отношение объема (25) к объему эллипсоида рассеяния определяется как эффектив­ность t. В случае многомерного нормального распределения, если — вектору среднего значения, то эффективен. Если включает и, и, то эффективность и S будет .

ЛИТЕРАТУРА

§ 3.2. Вот о, Рэфферти и Димер [1]; Д в а и е р [1]; Д е ш Рай [1], [2]; К е н д а л л [3], стр. 329—334, 337—339; Крамер [2]; Муд [2], стр. 186—188; К. Пирсон [1]; Стьюдент [1]; Ф ишер[10]; Фретс [1]; Хотеллинг [7];Хьюз [11; Чоун и Морэн [11]; Эйткен [31; Юл [2], [3].