
Корреляционный анализ
Корреляционным анализом называется метод выявления вероятностных связей между различными свойствами изучаемых объектов. Корреляционный анализ двух переменных называется парной корреляцией, а трех и более переменных – множественной корреляцией.
Основными задачами корреляционного анализа являются:
выяснение характера и тесноты корреляционных связей и их оценка с помощью коэффициентов корреляции и корреляционных отношений;
оценка значимости рассчитанных показателей связи;
сравнение показателей связи разных двумерных совокупностей.
Корреляционный анализ очень широко применяется в геологии. Наиболее часто он испо-льзуется при решении следующих задач:
оценке роли тех или иных факторов в различных геологических процессах для решения генетических вопросов;
выявлении парагенетических ассоциаций химических элементов и минералов в горных породах и рудах для оценки стадийности рудообразования, выделения геохимических и минералогических аномалий и т.п.;
изучении связей между концентрацией рудных элементов во вмещающих горных породах и рудах для выявления источников рудного вещества;
изучении связей между составом горных пород и руд и их физическими свойствами для рационального комплексирования поисковых геофизических методов;
выявлении связей между гранулометрическим, минералогическим составом и окатанностью обломочного материала для палеогеографического анализа условий формирования осадочных пород и т.д.
Корреляционный анализ может проводиться графическим, табличным и аналитическим способами.
Графический способ является наиболее простым и наглядным, поэтому изучение совокуп-ности двумерных величин обычно начинают с построения и анализа корреляционного графика.
Корреляционным графиком или полем корреляции называется график, на котором каждая пара исходных значений изображается точкой с координатами Ui и Vi (рис.5). Выбор одной из величин в качестве аргумента, а другой - в качестве функции определяется целью исследования. Например, при изучении связи между содержанием основного и попутного компонентов в руде в качестве аргумента выбирается содержание основного компонента, а в качестве функции – попутного.
Начало отсчета и масштаб по каждой оси выбирается по размаху варьирования каждого признака так, чтобы поле графика было квадратным или прямоугольным с отношением U : V не более 2:1.
Рис.5. Рис.6 Рис.7
С помощью корреляционного графика можно получить следующие очень ценные сведения о свойствах изучаемой двумерной величины.
График позволяет визуально оценить однородность выборки и выявить аномальные значения. Признаком неоднородности является разделение корреляционного поля на два, реже 3 самостоятельных поля (рис.6). Если поле неоднородное (рис.6), то исходную выборку следует разделить на соответствующее количество самостоятельных выборок и затем анализировать каждую из них отдельно. Признаком аномальности является значительное удаление точки от основной их массы на корреляционном поле. Аномальное значение целесообразно исключать из выборки. Аналитический способ исключения основан на расчете эллипса рассеяния для 95%-ной доверительной вероятности и отбраковке тех 5% значений, которые находятся за контурами эллипса (рис.7).
Форма и ориентировка корреляционного поля точек позволяет сделать вывод о наличии или отсутствии корреляционной связи, ее характере (прямая или обратная) и виде (линейная или нелинейная)
Признаком наличия корреляционной связи является вытянутость корреляционного поля точек в виде эллипса, непараллельного осям координат (рис.8), а признаком отсутствия связи – изометричность корреляционного поля (рис.9) или вытянутость эллипса рассеяния вдоль одной из осей координат (рис.10 и 11).
Рис.8 Рис.9 Рис.10 Рис.11 Рис.12 Рис.13
Характер связи определяется по направлению наклона длинной оси эллипса рассеяния. Признаком прямой (положительной) связи является наклон длинной оси эллипса в сторону возрастания аргумента (рис.12), а признаком обратной (отрицательной) связи – наклон этой оси в сторону уменьшения аргумента (рис.13).
Вид корреляционной зависимости (линейная или нелинейная) определяется по эмпирической линии регрессии. Для ее построения значения V группируют по классам значений U так, чтобы таких классов было не меньше 5 и в каждый класс попадало не меньше 5 пар значений. В каждом классе находят центры условных распределений (рис.14), которые должны находиться на пересечении двух взаимно перпендикулярных линий, соответствующим медианам U и V. Положение медиан определяют, перемещая по графику восковку с двумя взаимно перпендикулярными линиями, параллельными осям U и V, до такого положения, когда число точек в каждом классе по разные стороны от обоих перпендикуляров не окажется равным. Линия, соединяющая центры таких условных распределений, и является эмпирической линией регрессии. Ее форма и позволяет судить о виде корреляционной зависимости.
рис.14 рис.15 рис.16 рис.17
Корреляционное поле позволяет судить о симметрии или асимметрии распределения двумерной величины. Для этого на графике проводят две линии, соответствующие медианам U и V (как в предыдущем пункте – с восковкой). Если медианы пересекаются в центре графика с максимальным количеством точек на единицу площади, то распределение двумерной величины симметричное (рис.15) и близко к двумерному нормальному. Если же центр распределения и большинство точек смещены к началу координат, то распределение двумерной величины асимметричное, возможно, двумерное логнормальное (рис.16). В этом случае следует перестроить график в логарифмическом масштабе. Возможны случаи, когда распределение одной величины симметрично, а другой асимметрично.
Корреляционный график позволяет рассчитать приближенную оценку коэффициента корреляции методом дробового выстрела по корреляционному полю. Для этого корреляционное поле делится на 4 квадранта линиями, соответствующими медианам МеU и МеV (с помощью восковки). Квадранты нумеруются по ходу часовой стрелки, начиная с северо-восточного сектора (рис.17). В каждом квадранте подсчитывается количество точек n1, n2, n3 и n4, после чего рассчитывается тетрахорический коэффициент корреляции Бломквиста r по формуле:
 .
Однако эта оценка является приближенной.
Ее значение сравнивается с критическим
rкр., которое
зависит от уровня значимости
и объема выборки N.
Для =0,05
оно рассчитывается по формуле
.
Однако эта оценка является приближенной.
Ее значение сравнивается с критическим
rкр., которое
зависит от уровня значимости
и объема выборки N.
Для =0,05
оно рассчитывается по формуле
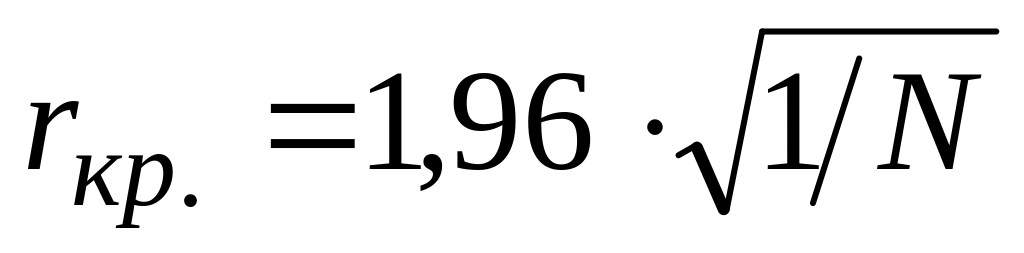 .
Если r>
rкр, то с
вероят-ностью 95% нулевая гипотеза об
отсутствии корреляционной связи
отвергается.
.
Если r>
rкр, то с
вероят-ностью 95% нулевая гипотеза об
отсутствии корреляционной связи
отвергается.
После предварительного исследования корреляционного графика приступают к аналитическому методу изучения корреляционной зависимости, который является наиболее полным и точным.
Аналитический метод заключается в расчете числовых характеристик распределения и связи и проверке гипотезы о значимости вычисленных показателей связи.
Основными числовыми характеристиками двумерного распределения являются:
числовые характеристики положения и рассеяния каждой из двух, входящих в двумерную совокупность, т.е. их математические ожидания МU и МV (или генеральные средние значения
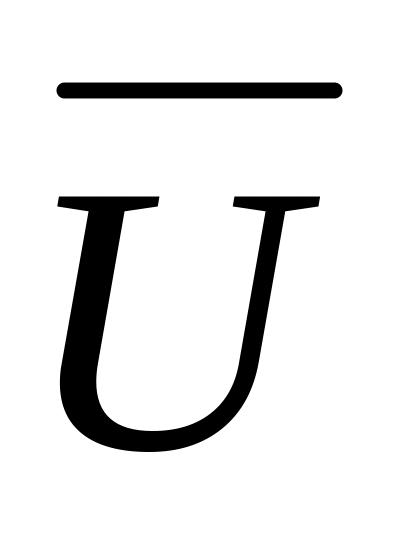 и
и
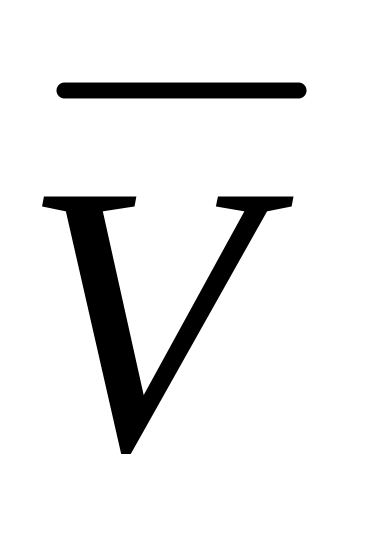 )
и дисперсии
)
и дисперсии
 и
и
 ,
а также условные математические
ожидания (условные средние
и
)
и условные дисперсии
и
;
,
а также условные математические
ожидания (условные средние
и
)
и условные дисперсии
и
;показатели связи величин U и V, т.е. числовые характеристики их взаимодействия, к которым относятся ковариация (или корреляционный момент), коэффициент корреляции и корреляционное отношение.
Средние значения и смещенные оценки
дисперсий величин U
и V рассчитываются по
формулам:
![]() ,
,
![]() ,
,
![]() и
и
![]() ,
а условные средние и условные дисперсии
- по формулам:
,
а условные средние и условные дисперсии
- по формулам:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Ковариация
(корреляционный момент или момент связи)
является мерой разброса двумерной
величины Ui-Vi
относительно общего центра распределения
![]() и по своему смыслу аналогична дисперсии
одномерной величины (рис.18).
и по своему смыслу аналогична дисперсии
одномерной величины (рис.18).
рис.18 рис.19
Ковариация
представляет собой среднее произведение
отклонений двух случайных величин от
их средних значений и является смешанным
моментом первого порядка. Ее смещенная
оценка рассчитывается по формуле:
![]() .
.
Из
сравнения формул дисперсии и ковариации
видно, что при Ui=Vi
ковариация становится равной дисперсии,
т.е. если оценить меру связи величины
Ui
или Vi
самой с собой, то ковариация превращается
в дисперсию:
![]() ,
,
![]() .
.
Это хорошо иллюстрируется следующей матрицей коэффициентов ковариации:
Ковариационная матрица |
Корреляционная матрица |
||||
Переменные |
U |
V |
Переменные |
U |
V |
U |
cov (U,U)=S2U |
cov (U, V) |
U |
|
|
V |
cov (V, U) |
cov (V,V)=S2V |
V |
|
|
Таким образом, элементы главной диагонали ковариационной матрицы представляют собой дисперсии величин, входящих в двумерную совокупность, а ковариации, расположенные на второй диагонали матрицы, равны друг другу, т.е. cov (U, V) = cov (V, U)
Ковариация имеет размерность самих изучаемых величин, что неудобно при сравнении моментов связи нескольких двумерных величин, особенно, если они имеют разные единицы измерения. Поэтому ее приводят к безразмерному стандартному виду, т.е. нормируют на произведение стандартных отклонений величин U и V. Такая ковариация, нормированная по стандартам, называется коэффициентом корреляции.
Таким
образом, коэффициент корреляции
представляет собой отношение ковариации
к произведению стандартных отклонений
изучаемых величин U
и V:
![]() или
или
 ,
,
где
cov (U, V)
– ковариация величин Ui
и Vi,
![]() и
-
их средние значения, SU
и SV
– выбороч-ные оценки средних квадратических
отклонений.
и
-
их средние значения, SU
и SV
– выбороч-ные оценки средних квадратических
отклонений.
При расчете коэффициента корреляции могут использоваться как смещенные, так и несмещенные оценки ковариации и стандартов, поскольку значения N в числителе и знаменателе формулы взаимно сокращаются.
Однако
эти формулы удобны только для
понимания сути корреляционного
анализа, но не для вычислений. Практические
же расчеты коэффициента корреляции
проводятся по формуле: 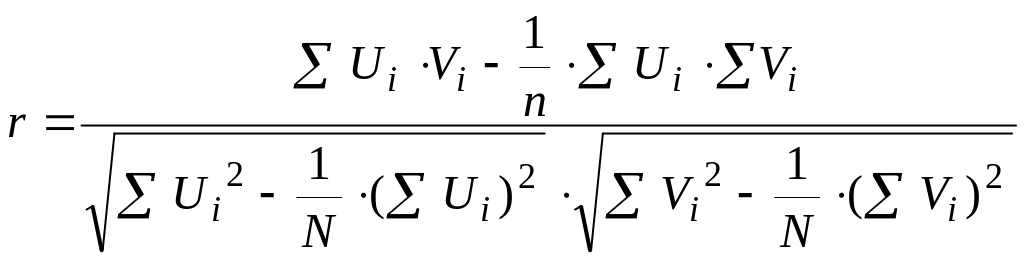 ,
т.е.
,
т.е.
![]() .
.
При преобразовании ковариационной матрицы в корреляционную элементы главной диагонали становятся равными 1, а элементы второй диагонали равны друг другу, т.е. ruv = rvu.
Следует отметить, что на вычисленный
коэффициент корреляции очень сильно
влияют аномальные значения
двумерной совокупности. Для их исключения
из выборки используется эллипс рассеяния
двумерного нормального распределения.
Эллипс строится по уравнению, которое
получают из выражения
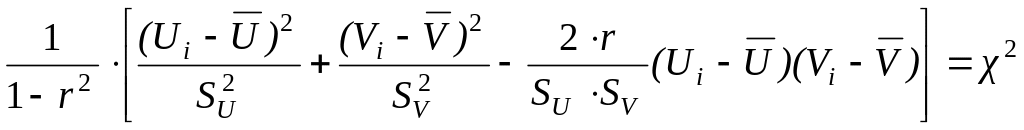 .
.
В этом уравнении значение 2 выбирается, исходя из заданного уровня значимости . В частности, для =0,05 (т.е. при 95%-ной доверительной вероятности) 2=6,0516. Аномальными считаются значения, выходящие за пределы контурного эллипса, построенного на корреляционном графике (рис.19). При 2 =6,0516 количество таких точек не превысит 5%.
Корни квадратного уравнения эллипса рассеяния двумерной величины U-V, составленного для 5%-го уровня значимости, можно рассчитать по формуле (Мягков и др., 1989)
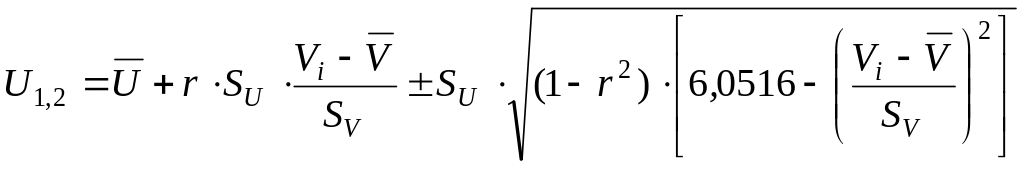 .
.
После исключения аномальных значений следует снова рассчитать все статистики расп-ределения и связи без учета выдающихся значений.
Значимость выборочного коэффициента корреляции оценивается несколькими способами.
С помощью t-критерия Стьюдента по формуле
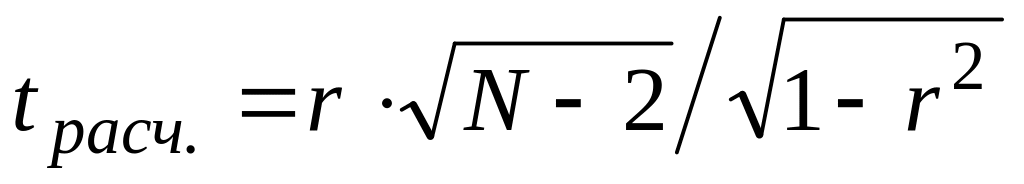 .
Если tрасч.>
tтеор.
для принятого уровня значимости
и при числе степеней свободы f=N–2,
то нулевая гипотеза об отсутствии
корреляционной связи отвергается и
связь считается статистически значимой
(реальной).
.
Если tрасч.>
tтеор.
для принятого уровня значимости
и при числе степеней свободы f=N–2,
то нулевая гипотеза об отсутствии
корреляционной связи отвергается и
связь считается статистически значимой
(реальной).
С помощью среднеквадратической погрешности r оценки коэффициента корреляции, которая рассчитывается по формулам: при N<50
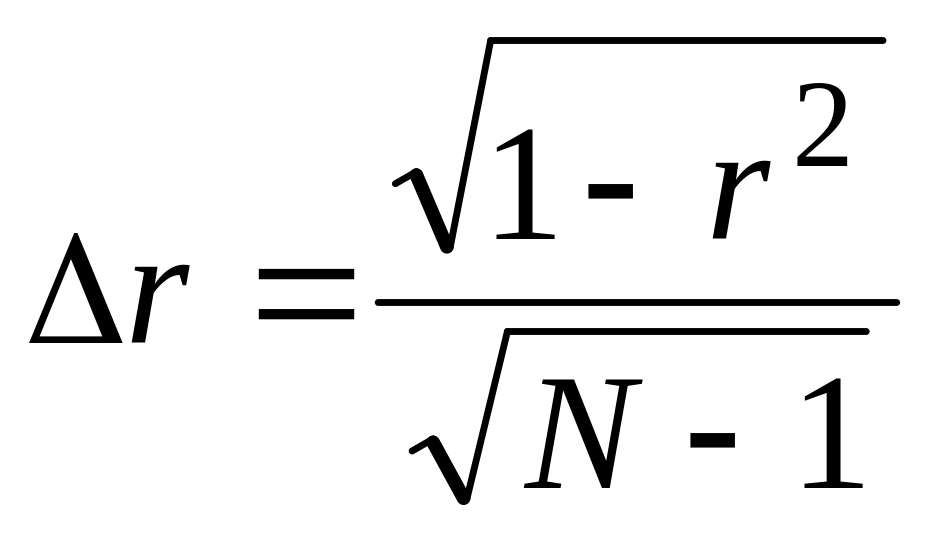 ;
;
при N>50
![]() .
Если
r
tr,
где t – коэффициент
вероятности для принятого уровня
значимости ,
то связь считается статистически
значимой. В частности, при =0,05
(т.е. вероятности 95%) t=2
и выражение имеет вид
r
2r.
При =0,01
(т.е. вероятности 99%) t=3.
.
Если
r
tr,
где t – коэффициент
вероятности для принятого уровня
значимости ,
то связь считается статистически
значимой. В частности, при =0,05
(т.е. вероятности 95%) t=2
и выражение имеет вид
r
2r.
При =0,01
(т.е. вероятности 99%) t=3.
По таблице критических значений коэффициентов корреляции. Корреляционная связь считается статистически значимой, если rрасч.> rкрит. для принятого уровня значимости .
При интерпретации выявленной связи следует помнить о следующих свойствах коэффи-циента корреляции:
коэффициент корреляции изменяется от –1 до +1 (-1 r +1);
при прямой зависимости r >0, при обратной r < 0;
равенство r =1 соответствует линейной функциональной связи;
равенство r =1 свидетельствует об отсутствии только линейной связи, но не связи вообще (нелинейной);
по тесноте различают следующие типы корреляционных связей:
а) очень тесная 0,75 < r < 1,0; в) слабая при 0,25 < r < 0,5 ;
б) тесная при 0,5 < r < 0,75 ; г) связь отсутствует r <0,25 .
Следует помнить, что коэффициент корреляции очень чувствителен к виду функций расп-ределения величин, входящих в двумерную совокупность. Поэтому, если эти распределения заметно отличаются от нормальных, то коэффициент корреляции следует рассчитывать не по исходным, а предварительно нормализованным значениям двумерной величины.
