Методы Деформации поверхностей

Численные методы, используемые в задачах аэродинамики, можно условно разделить на два класса √ сеточные методы и бессеточные методы. Сеточные методы имеют лучшее математическое обоснование, высокую точность и ряд других преимуществ. Однако их применение требует больших вычислительных затрат, а также предполагает достаточно трудоемкую процедуру создания сетки во всей расчетной области, размеры которой подчас выбираются достаточно большими для уменьшения влияний граничных условий. Их приложение к задачам аэродинамики деформируемых поверхностей требует использования подвижных деформируемых сеток, что приводит к дополнительным трудностям и увеличивает время счета. Поэтому в задачах аэродинамики деформируемых поверхностей предпочтительней применение бессеточных методов. Они имеют менее строгое математическое обоснование (зачастую их относят к методам моделирования), но требуют на порядок меньших вычислительных затрат, не накладывают ограничений на размер расчетной области, позволяют автоматически удовлетворять условиям ⌠на бесконечности■.

Одним из наиболее распространенных на сегодняшний день бессеточных методов аэродинамики несущих поверхностей является метод дискретных вихрей (см., например, /1/). Однако для его применения к задачам обтекания деформируемых поверхностей требуется ряд модификаций. Часть из них уже была описана в /2/. Это, прежде всего, учет дополнительных относительных скоростей в контрольных точках, возникающих вследствие деформации поверхности. Кроме того, если закон деформации поверхности в общем виде не известен, то для определения направления нормалей к поверхности в контрольных точках требуется некоторая аппроксимация, например, предложенная в /2/ кусочно-квадратичная аппроксимация.

В случае, если обтекание деформируемой поверхности носит отрывной характер, требуются дополнительные модификации. Под отрывным в данном случае понимается обтекание, при котором вихревая пелена сходит не только с задней и боковых кромок поверхности, но и с передней кромки или некоторой ее части. При этом размер и положение отрывной зоны на передней кромке могут меняться со временем. Так как метод дискретных вихрей предполагает предварительное задание линий отрыва, то необходим некоторый критерий, по которому можно было бы судить о характере обтекания на рассматриваемом участке передней кромки. В данной работе в качестве такого критерия предлагается мгновенный местный угол атаки a il, определяемый в контрольной точке на передней кромке как a il = arctg{(v× n)/[v× (n´ t)]}. Здесь n √ единичный вектор нормали к поверхности (известен в контрольной точке); t √ единичный вектор касательной к линии передней кромки, который может быть легко определен по известным координатам узлов вихревой сетки, окружающих рассматриваемую контрольную точку. Вектор v представляет собой сумму вектора скорости невозмущенного набегающего потока v¥ и дополнительной относительной скорости, возникающей в силу деформации поверхности vd. Если на соответствующем участке передней кромки происходит отрыв, то на передней кромке размещается контрольная точка и свободный вихрь.

Другая важная модификация касается расчета поля давления. Для нахождения давления во всей расчетной области требуется введение сеточных процедур, однако, на практике в этом, как правило, нет необходимости. Поэтому целесообразно ограничиться определением перепада давления на обтекаемой поверхности (аэродинамической нагрузки). В методе дискретных вихрей для этого используется интеграл Коши-Лагранжа (в /2/ было предложено вычислять его в контрольных точках)

D p = p+ - p- = ½ g ´ v0½  - 2¶ D j /¶ t.

Здесь p+ и p- - соответственно давления на верхней и нижней сторонах поверхности, g - вектор распределенной поверхностной интенсивности вихрей, D j  = j + - j - - скачок потенциала скорости при переходе через поверхность. Обычно D j определяют как циркуляцию вектора скорости по достаточно большому замкнутому контуру, пересекающему систему присоединенных и свободных вихрей только в рассматриваемой точке. Однако в случае отрыва с передней кромки выбор такого контура затруднен. В связи с этим предлагается вычислять D j непосредственно, вводя для этих целей фиктивную толщину поверхности D f , влияющую только на расчет потенциала скорости. Тогда для скачка потенциала в рассматриваемой точке поверхности О получаем

,

где r √ расстояние от точки О, отсчитываемое по нормали к поверхности.

Значение D f определяется порядком меры дискретности метода D (минимальное расстояние от контрольной точки до ближайшего присоединенного вихря /1/).

На рис. 1 приведены значения коэффициента нормальной силы Cy плоского крыла с удлинением 1, определенные экспериментальным /1/ и расчетным путем. Расчет проводился для разных значений D f при D  = 0,05.

Как видно из рисунка, с ростом углов атаки влияние величины D f на рассчитанные значения аэродинамической нагрузки быстро уменьшается. Если для углов атаки, на которых отрывное обтекание только начинает развиваться, т.е. для углов порядка 10-15° , еще можно говорить о некотором оптимальном значении величины D f (при данном значении D ), обеспечивающем наилучшее совпадение результатов расчетов с экспериментом, то для больших углов атаки выбор величины D f уже не влияет на результаты расчетов. Единственным ограничением при этом является D f£ D .

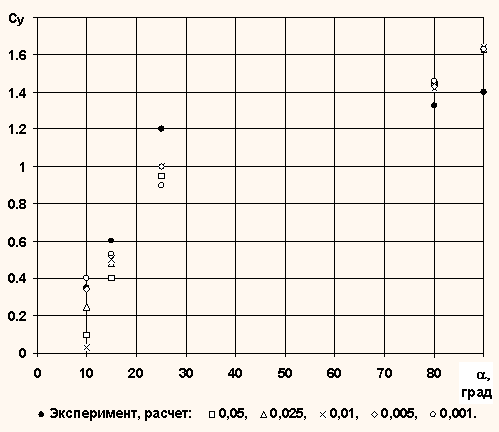
Рис. 1. Влияние значения фиктивной толщины на коэффициент нормальной силы для различных углов атаки

Предлагаемые модификации позволяют существенно расширить класс задач, решаемых с помощью метода дискретных вихрей, за счет задач, в которых характер обтекания (безотрывное или с отрывом на передней кромке), а также размер и положение отрывных зон меняются со временем. К такого рода задачам (задачам с динамическим отрывом) относятся, например, задачи аэродинамики колеблющегося или машущего крыла.