
- •10) Равномерное и показательное распределения нсв: функция распределения, плотность, основные параметры распределения, числовые характеристики, вероятность попадания на интервал.
- •12) Распределение χ2 Пирсона, f- распределение Фишера, t- распределение Стьюдента; основные параметры этих распределений, графики.
- •13) Неравенства Маркова и Чебышева, лемма о среднем арифметическом случ.Величин.
- •14)Закон больших чисел. Центральная предельная теорема.
- •18)Графическое представление выборки:
- •20. Точечные оценки математического ожидания и дисперсии:
- •21. Методы нахождения оценок: метод моментов
18)Графическое представление выборки:
Гистограмма: Ступенчатая фигура,
состоящая из прямоугольников с
основаниями длиной
 и высотами
и высотами
 (плотность частоты), называется
гистограммой частот.
(плотность частоты), называется
гистограммой частот.
Полигон частот: Ломаная, отрезки
которой соединяют точки
 ,
называется полигоном частот. Ломаная,
соединяющая на координатной плоскости
точки
,
называется полигоном частот. Ломаная,
соединяющая на координатной плоскости
точки
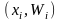 ,
называется полигоном относительных
частот.
,
называется полигоном относительных
частот.
19. Несмещенной называется
статистическая оценка
 ,
математическое ожидание которой равно
оцениваемому параметру
,
математическое ожидание которой равно
оцениваемому параметру
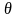 при любой выборке:
при любой выборке: (3.6).
Смещенной называется оценка, при
которой условие (3.6) не выполняется.
(3.6).
Смещенной называется оценка, при
которой условие (3.6) не выполняется.
Эффективной называется оценка,
которая имеет минимальную дисперсию
при заданном объеме выборки п.
Состоятельной называется
статистическая оценка типа
 ,
которая при
,
которая при
 стремится к оцениваемому параметру.
стремится к оцениваемому параметру.
20. Точечные оценки математического ожидания и дисперсии:
Состоятельная несмещенная оценка математического ожидания генеральной совокупности по выборке объема n:

Состоятельная несмещенная оценка дисперсии генеральной совокупности по выборке объема n при неизвестном математическом ожидании:
 «исправленная дисперсия»
«исправленная дисперсия»Состоятельная несмещенная оценка дисперсии генеральной совокупности по выборке объема n при известном математическом ожидании а генеральной совокупности:

Состоятельная смещенная оценка дисперсии генеральной совокупности по выборке объема n при неизвестном математическом ожидании:

Свойства точечных оценок:
1о.
 . 2о.
а)
. 2о.
а)
 б)
б)
 .
.
3о.
Если
 ,
где с – некоторая константа, то а)
,
где с – некоторая константа, то а)
 ;
б)
;
б) ,
где
,
где
 .
.
21. Методы нахождения оценок: метод моментов
Метод
моментов заключается в следующем: любой
момент случайной величины
![]() (например,
(например,
![]() -й)
зависит, часто функционально, от
параметра
-й)
зависит, часто функционально, от
параметра
![]() .
Но тогда и параметр
может
оказаться функцией от теоретического
-го
момента. Подставив в эту функцию вместо
неизвестного теоретического
-го
момента его выборочный аналог, получим
вместо параметра
оценку
.
Но тогда и параметр
может
оказаться функцией от теоретического
-го
момента. Подставив в эту функцию вместо
неизвестного теоретического
-го
момента его выборочный аналог, получим
вместо параметра
оценку
![]() .
Пусть
,
.
Пусть
,
![]() ,
,
![]() —
выборка объема
—
выборка объема
![]() из
параметрического семейства распределений
из
параметрического семейства распределений
![]() ,
где
,
где
![]() .
Выберем некоторую функцию
.
Выберем некоторую функцию
![]() так,
чтобы существовал момент
так,
чтобы существовал момент
|
(3) |
и
функция
![]() была
обратима в области
была
обратима в области
![]() .
Тогда в качестве оценки
для
возьмем
решение уравнения
.
Тогда в качестве оценки
для
возьмем
решение уравнения
![]()
Или (что то же самое), сначала решаем уравнение (3) относительно , а затем вместо истинного момента берем выборочный:
![]()
Чаще
всего в качестве функции
берут
![]() .
В этом случае
.
В этом случае
![]()
и, если функция обратима в области , то

Можно сказать, что мы берем в качестве оценки такое (случайное) значение параметра , при котором истинный момент совпадает с выборочным.
Методы нахождения оценок: метод максимального правдоподобия
Метод
максимального правдоподобия — еще
один разумный способ построения оценки
неизвестного параметра. Состоит он в
том, что в качестве «наиболее
правдоподобного» значения параметра
берут значение
,
максимизирующее вероятность получить
при
опытах
данную выборку
![]() .
Это значение параметра
зависит
от выборки и является искомой оценкой.
.
Это значение параметра
зависит
от выборки и является искомой оценкой.
Решим
сначала, что такое «вероятность получить
данную выборку», т.е. что именно нужно
максимизировать. Вспомним, что для
абсолютно непрерывных распределений
их
плотность
![]() —
«почти» (с точностью до
—
«почти» (с точностью до![]() )
вероятность попадания в точку
)
вероятность попадания в точку
![]() .
А для дискретных распределений
вероятность
попасть в точку
равна
.
А для дискретных распределений
вероятность
попасть в точку
равна
![]() .
И то, и другое мы будем называть плотностью
распределения
.
Итак,
.
И то, и другое мы будем называть плотностью
распределения
.
Итак,
22.
Интервал
 ,
в который с вероятностью р попадает
параметр
,
в который с вероятностью р попадает
параметр
 ,
называется доверительным интервалом
параметра
с уровнем доверия р,т.е.
,
называется доверительным интервалом
параметра
с уровнем доверия р,т.е.

Квантилем
уровня р называется такое число xp,
для которого выполняется равенство

Для оценки M и D используют следующие квантили:
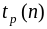 –
квантиль
распределения Стьюдента;
–
квантиль
распределения Стьюдента;
 –
квантиль
распределения Пирсона, значения которых
приведены в Приложениях (табл. П.5, П.4
соответственно).
–
квантиль
распределения Пирсона, значения которых
приведены в Приложениях (табл. П.5, П.4
соответственно).
Теорема.Пусть
задано число Тогда при достаточно большом объеме
выборки параметры М и D
имеют следующие доверительные интервалы:
Тогда при достаточно большом объеме
выборки параметры М и D
имеют следующие доверительные интервалы:

Число
 – вероятность ошибки Ι рода, называется
уровнем значимости. Обычно при
фиксированном объеме выборки уровень
значимости задан. Снижение вероятностей
ошибок Ι и ΙΙ рода возможно за счет
увеличения объема выборки.
– вероятность ошибки Ι рода, называется
уровнем значимости. Обычно при
фиксированном объеме выборки уровень
значимости задан. Снижение вероятностей
ошибок Ι и ΙΙ рода возможно за счет
увеличения объема выборки.
 .
.
23.


Или
23) Интервальные оценки
математического ожидания а и дисперсии
D нормально
распределенной генеральной совокупности
по выборке объема n
с надежностью
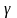 1*.
При известном среднем квадратическом
отклонении
генеральной
совокупности
1*.
При известном среднем квадратическом
отклонении
генеральной
совокупности
 ,
где
,
где
 значение
аргумента функции Лапласа
значение
аргумента функции Лапласа
 ,
при котором
,
при котором

или
 ,
где
,
где
 точность
оценки.2*. При
неизвестном среднем квадратическом
отклонении (и объеме выборки
точность
оценки.2*. При
неизвестном среднем квадратическом
отклонении (и объеме выборки
 )
)
 ,
где
,
где

 квантиль
распределения Стьюдента уровня p
с k степенями свободы
(находится по таблице).
квантиль
распределения Стьюдента уровня p
с k степенями свободы
(находится по таблице).
3*. При неизвестном
среднем квадратическом отклонении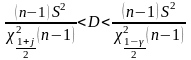
. 4*. При известном математическом ожидании а

24)Проверка статистических гипотез о виде закона распределения с помощью критерия Пирсона х^2: Статистическая гипотеза – это предположение относительно того, каков закон распределения некоторой случайной величины, каковы величины независимых параметров закона распределения случайной величины и т.д.
Выдвигаем гипотезу
 .
Вычисляем по выборке
.
Вычисляем по выборке
 меру расхождения эмпирических частот
меру расхождения эмпирических частот
 и теоретических частот
и теоретических частот
 ,
соответствующих гипотезе
,
где
,
соответствующих гипотезе
,
где
 теоретическая
вероятность попадания в i-й
интервал, вычисленная в условиях
гипотезы
.
теоретическая
вероятность попадания в i-й
интервал, вычисленная в условиях
гипотезы
.
Находим по таблице распределения
Пирсона квантиль
 ,
где m – число
интервалов вариационного ряда, r
– число параметров распределения,
вычисленных по экспериментальным
данным.
,
где m – число
интервалов вариационного ряда, r
– число параметров распределения,
вычисленных по экспериментальным
данным.
Если
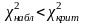 ,
то гипотеза
,
то гипотеза
 принимается.
В противном случае гипотеза
отвергается и принимается альтернативная
гипотеза.
принимается.
В противном случае гипотеза
отвергается и принимается альтернативная
гипотеза.
