Путеводитель по алгебре
для учащихся 8 класса
общеобразовательных учреждений
«Решение рациональных неравенств методом интервалов»
Составитель:
Шулятьева Л.В. – учитель математики высшей категории
МБОУ «Гимназия №1»
г. Чебоксары
2012
Решение рациональных неравенств методом интервалов.
Алгебраическим выражением называется совокупность конечного количества чисел, обозначенных буквами или цифрами, соединенных между собой знаками алгебраических действий и знаками последовательности этих действий (скобками).
Алгебраическое выражение, в котором указаны только действия сложения, вычитания, умножения и возведения в степень с натуральным показателем, называют целым рациональным выражением.
Если кроме указанных действий входит действие деления, то выражение называют дробно-рациональным.
Всякое значение переменной, при котором данное неравенство с переменной обращается в верное числовое неравенство, называется решением неравенства.
Решить неравенство — значит найти все его решения или же доказать, что их не существует.
Совокупность решений неравенства именуется множеством решений неравенства.
Е
сли
в разложении многочлена на множители
входит сомножитель
,
то говорят, что
- корень многочлена кратности
.
Пример.
А(х) =
Данный многочлен
имеет корни:
кратности 6;
кратности 3;
кратности 1;
кратности 2;
кратности 5.
Теорема. Непрерывная функция, не обращающаяся в нуль на некотором интервале, сохраняет на этом интервале постоянный знак.
Решение целых рациональных неравенств с одной переменной методом интервалов
Метод интервалов основан на свойствах функции и заключается в следующем:
Пусть дано неравенство А(х)>0 (вместо знака > могут стоять знаки <, ≥, ≤.),
г
де
А(х) – многочлен стандартного вида (1 )
или выражение вида (2)
План решения:
Если неравенство не имеет вид (1) или (2), то приведем его к этому виду: перенесем все слагаемые в левую часть, а в правой части оставить нуль.
Найдем корни уравнения А(х)=0
;
;
...;
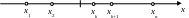Нанесем корни уравнения на числовую прямую.
Эти корни разбивают числовую прямую на n+1 промежуток, на каждом из которых левая часть неравенства A(x)>0 сохраняет знак (то есть во всех точках промежутка либо A(x)>0, либо A(x)<0), поскольку, по свойствам функции, изменить знак она может только при переходе через корни – нули функции f(x)=А(х).
Замечание 1. Корни четной кратности подчеркнуть двойной чертой.
Н
айдем
знак левой части неравенства на каждом
из полученных интервалов. Для этого на
одном из интервалов выберем какое-то
значение x=x0
и, подставив это значение в левую часть
неравенства, определим знак А(х) на
выбранном интервале (метод пробных
точек), а потом учесть, что:
а) А(х) меняет знак при переходе от одного промежутка к соседнему через корень нечетной кратности;
б) А(х) не меняет знак при переходе через корень четной кратности.
Выберем те промежутки, где выполняется заданное неравенство (отметим их штрихами - заборчиком).
Замечание 3. В случае A(x)0 (А(х)≤0) корни уравнения A(x)=0 являются решениями неравенства (закрашенные точки на числовой прямой). При записи ответа надо обращать внимание на «одиноко стоящие закрашенные точки», которые не вошли в отмеченные промежутки решения, и добавить их в ответ.
Пример.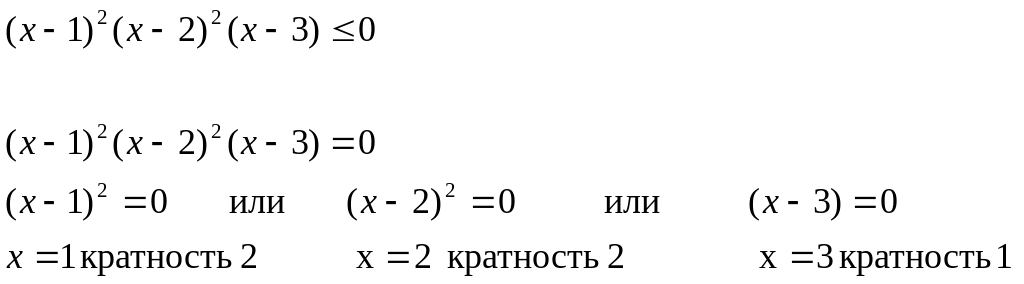 
-
+
+
+
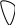
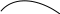
х
1
2
3
4. Запишем ответ.
Рассмотрим примеры решения неравенств методом интервалов.
Пример 1. Решить неравенство методом интервалов (x–6)(x+3)0
Решим уравнение:
(
x–6)(х+3)=0
Нанесем полученные корни на числовую прямую, причем, так как неравенство нестрогое и эти корни являются решениями и неравенства, изобразим их черными точками.
3. Найдем знак левой
части на промежутке [6; +):
х=7, А(7)=(7–6)(7+3)=110=10>0 А(х)>0;
4. Нашему неравенству удовлетворяют два промежутка: (–; –3] и [6; +)
Ответ: (–; –3] [6; +).
Пример 2. Решить неравенство методом интервалов
–х2–2х+48<0
Разложим левую часть неравенства на множители
–х2–2х+48=0 х2+2х–48=0
Для решения этого квадратного уравнения воспользуемся теоремой Виета.
.
Разложим квадратный трехчлен –х2–2х+48 на множители: –х2–2х+48=−(х+8)(х–6), таким образом имеем неравенство –(х+8)(х–6)<0.