2.3. Проверка гипотезы о нормальном распределении случайной величины

Законы распределения случайных величин отражают Физическую сущность рассматриваемых явлений. Совокупность факторов и усло­вий, приводящих к возникновению того или другого вероятностного закона, называют математической моделью. Применительно к нор­мальному закону математической моделью служат следующие усло­вия:

исследуемое явление является следствием или суммой воз­действия достаточно большого количества различных случайных, независимых между собой или слабо зависимых источников;

дисперсии и математические ожидания складываемых источни­ков мало отличаются друг от друга и от математического ожидания и дисперсии складываемой суммы.

При наличии указанных условий возникает нормальный закон, находящий широкое применение при решении различных экономиче­ских и инженерных задач. Применительно к математической теории надежности нормальный закон хорошо описывает постепенные отказы изделий, вызываемые выходом из строя их отдельных элементов. В теории массового обслуживания нормальный закон хорошо опи­сывает случайное время обслуживания заявки, связанное с выполнением ряда операций. Так, нормальному закону соответствуют распределения продолжительности обслуживания автотранспортных средств в пунктах погрузки и разгрузки, интервалов движения между автобусами на маршрутах, скоростей движения однотипных автомобилей в транспортном потоке и т.д.

Плотность вероятности нормального распределения опреде­ляется следующим выражением:

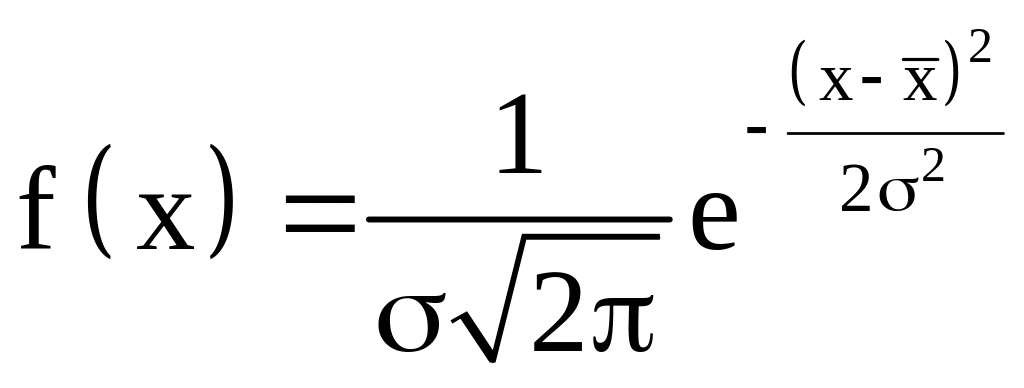, (2.5)

где x - случайная величина;

- математическое ожидание, т.е. среднее значение рассматриваемой случайной величины;

σ - среднее квадратическое отклонение, характери­зующее разброс случайной величины относительно её математического ожидания. Существует довольно большое количество методик проверки нормальности распределения опытных данных. Для практического применения рекомендуется [II] две методики: по размаху варьирования и по χ² - критерию, причем первая служит для быстрой "прикидочной" проверки, а вторая - для основательной проверки нормальности распределения.

Быструю проверку гипотезы нормальности распределения для сравнительно широкого класса выборок 3 < N < 1000 можно выполнить с помощью метода, изложенного в [8], исполь­зуя размах варьирования R. Подсчитывают отношение R/S и сопоставляют с критическими верхними и нижними границами этого соотношения, приведенными в табл. IV приложения. Если R/S меньше нижней и больше верхней границы, то нормального распределения нет. Особенно важно, чтобы это условие соблюдалось при α= 0,1 (10 % -ный уровень значимости). В рассматриваемом в первой главе примере

.

При N = 100 и α = 0,1 нижняя и верхняя границы по табл. IV приложения соответственно равны 4,44 и 5,68, т.е. 4,44 < 4,77 < 5,68. Следовательно, гипотеза нормальности распре­деления подтверждается по первому "прикидочному" критерию. Рассмотрим теперь методику проверки гипотезы нормаль­ности распределения по χ² - критерию. Первоначально вы­числяют статистические характеристики (статистическое мате­матическое ожидание и статистическую дисперсию) и принимают указанные характеристики для сглаживающего ряда. На осно­вании статистических критериев Пирсона, Романовского прове­ряют правдоподобность принятой гипотезы. При расчетах статистических характеристик используем резуль­таты, полученные в предыдущей главе, все полученные данные заносим в табл. 2.1.

1. Вычисляем опытные частости, для чего частоты делим на число всех испытаний

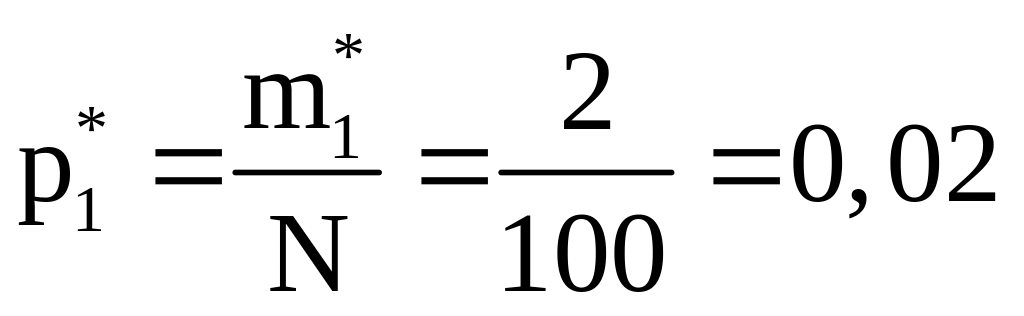; и т.д.

2. Вычисляем статистическое математическое ожидание скоростей движения автомобилей

3. Вычисляем статистическую дисперсию

При этом несмещенное значение среднего квадратического отклонения

.

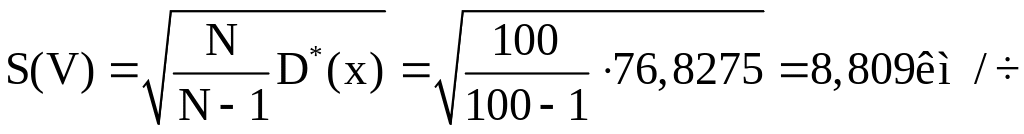Таким образом, экспериментальное распределение будем вырав­нивать нормальным законом следующего вида:

4. Вычисляем теоретические вероятности попадания слу­чайной величины в интервалы по формуле

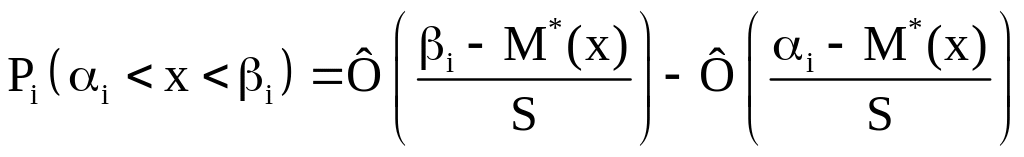, (2.6)

где α_i, β_i - границы i - интервала;

М^*(x) - математическое ожидание;

S - стандартное отклонение ;

- функция Лапласа.

При вычислении табличных значений Функции Лапласа используется линейная интерполяция. Как правило, математические таблицы содержат значения табулируемой функции f(x) для равноотстоящих друг от друга дискретных значений аргумента, которые принято называть опорными точками. Так в табл.1 прило­жения приведены значения функции Гаусса φ(z) и функции Лапласа Ф(z) для значений аргумента z = 0; 0,1; 0,2; 0,3 и т.д. Однако на практике часто возникает необходимость опре­деления величины f(x) для промежуточных значений аргумен­та x , лежащих между соседними опорными точками.

Простейшим методом определения величины f(x) для произвольного значения аргумента X = X^* , лежащего между со­седними опорными точками Х₀ и Х₁ (Х₀ < X^* < Х₁ ), является метод линейной интерполяции, основанный на соотно­шении

f(х^*) = (1 - h) f(х₀) + h ∙ f(х₁), (2.7)

где f(х^*) - искомое значение функции при X = X^*;

f(х₀), f(х₁) - значения табулированной функции в соседних опорных точках Х₀ и Х₁;

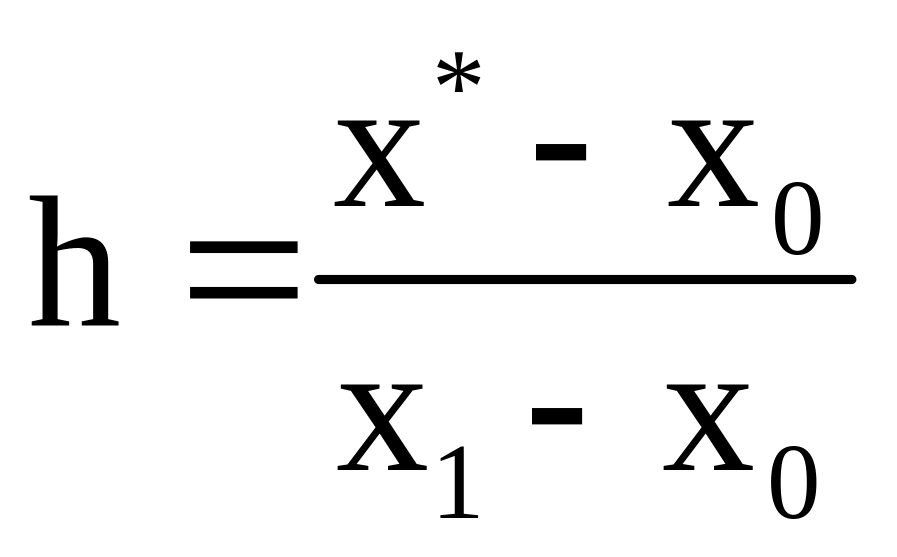
В качестве примера определим значение функции Лапласа при X^* = 0,641, пользуясь табл.1 приложения и методом линейной интерполяции. Поскольку интересующее нас значение аргумента X^* = 0,641 лежит между соседними опорными точками Х₀ = 0,6 и Х₁ = 0,7, находим величину

и согласно (2.7) находим

Ф (0,641) ≈ (1 - 0,41) ∙ Ф (0,6) + 0,41∙ Ф (0,7) = 0,59 ∙ 0,2257 + 0,41∙ 0,2580 = 0,239

Таблица 2.1

Статистическая обработка экспериментальных данных - скоростей движения автомобилей

Номер разряда	Границы интерва­лов скоростей движения (αi - βi), км/ч	Сере­дины интер­валов Vci, км/ч	Опыт­ные часто­ты	Опыт­ные часто­сти	Теорети­ческие вероятно­сти P (αi<V<βi)	Теоретичес­кие числа попадания V в интер­валы	Слагаемые критерия Пирсона
I	2	3	4	5	6	7	8
I	26 - 30	27,5	2	0,02	0,038	3,8	0,85
2	30 - 35	32,5	13	0,13	0,091	9,1	1,67
3	35 - 40	37,5	18	0,18	0,171	17,1	0,05
4	40 - 45	42,5	24	0,24	0,215	21,5	0,29
5	45 - 50	47,5	19	0,19	0,210	21,0	0,19
6	50 - 55	52,5	11	0,11	0,146	14,8	0,98
7	55 - 60	57,5	8	0,08	0,075	7,5	0,03
8	60 - 65	62,5	3	0,03	0,029	2,9	0,01
9	65 - 70	67,5	2	0,02	0,007	0,7	2,41
Итоговая строка			==100	==1,0			χ^2= 6,48

При вычислении теоретических вероятностей попадания случайной величины в соответствующие интервалы используем вспомогательную таблицу 2.2, в первую строку которой заносим значения границ интервалов γ_i. Во вторую строку таблицы помещаем вычисленные значения

.

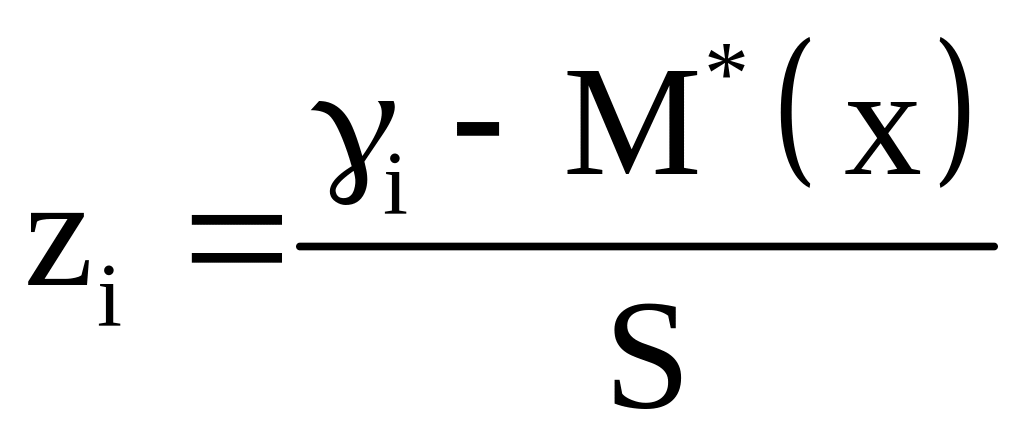Так для γ = 50, .

Пользуясь табл. 1 приложения и методом линейной интерполяции, вычисляем значения функции Лапласа Ф(z_i) при расчетах, учиты­ваем, что функция Лапласа нечетная, Ф(-x) = - Ф(x). Вычитая из каждого последующего значения Ф(z_i+1) предыдущее Ф(z_i), получаем искомые теоретические вероятности P_i (α_i < V < β_i)

Таблица 2.2

γi	25	30	35	40	45	50	55	60	65	70
zi	2,197	1,629	1,061	0,494	0,074	0,641	1,209	1,777	2,344	2,912
Ф(zi)	0,486	0,448	0,357	0,186	0,029	0,239	0,387	0,462	0,491	0,498
Рi	0,038	0,091	0,171	0,215	0,210	0,148	0,075	0,029	0,007

5. На основе полученных поинтервальных теоретических вероятностей P_i производим выравнивание гистограммы опытных данных теоретической кривой нормального закона (рис. 2.3)

6. Находим теоретические числа попадания случайной величины в интервалы

m_i = p_i N.

Получаем m₁ = p₁ N = 0,038 ∙ 100 > 3,8; m₂ = 0,091 ∙ 100 = 9,1.

Результаты вычислений заносим в столбец 7 табл. 2.1.

42

Рис. 2.3. Гистограмма распределения частостей попадания скоростей движения автомобилей (1) и выравнивающая её теоретическая кривая нормального закона (2).

7. Рассчитываем значение χ² - квадрат Пирсона

.

Для первого интервала

.

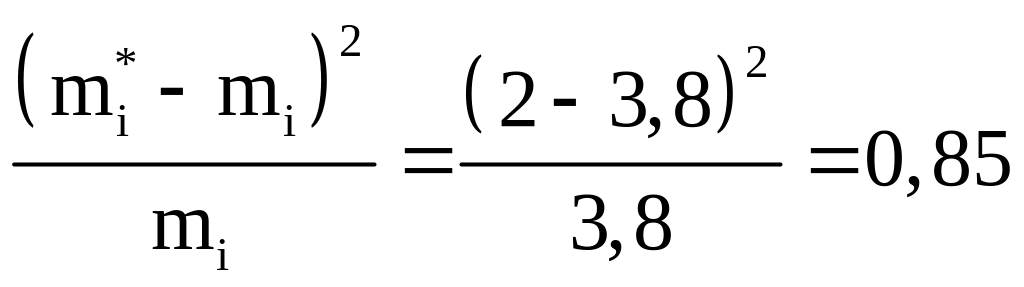Для второго интервала

.

Суммируя значения столбца 8, получаем χ² = 6,48.

8. Проверяем правдоподобность гипотезы о принадлежности опытных данных к нормальному закону с помощью критерия Пирсона. Для рассматриваемого примера число степеней свободы К = n - S = 9 - 3 =6 и заданный уровень значимости 0,05. По табл. V при­ложения находим Р (χ², К) = Р (6,48; 6) = 0,374 > 0,05. Следовательно, по критерию Пирсона гипотеза о принадлежности опытных данных к нормальному закону не отвергается. Аналогичный результат получим, если проверка гипотезы будет производиться с помощью табл. VI приложения.

Для числа степеней К = 6 и уровня значимости α = 0,05

К_теор = 12,5 > К_опыт = 6,48.

9. Проверяем правдоподобность принятой гипотезы с помощью критерия Романовского

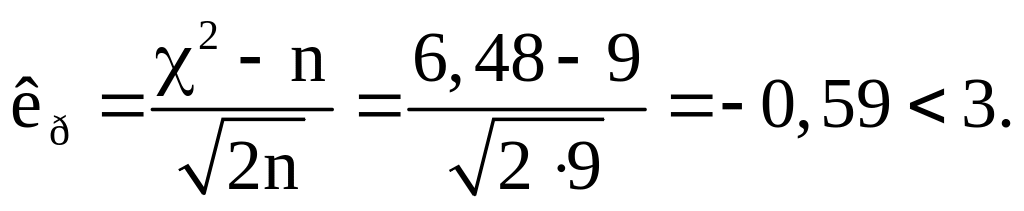
Как видим, и по критерию Романовского гипотеза о принадлеж­ности опытных данных к нормальному закону не отвергается.