Комбинаторный принцип умножения.

Представьте себе, что человек, которому не чем больше заняться, подбрасывает монету и кость (в виде игрального кубика). На монете может выпасть "орел" (О) и "решка" (Р). При падении кости возможные исходы представляют собой 1,2,3,4,5 и 6. Возможными исходами обоих событий являются (О,1), (О,2), (О,3), (О,4), (О,5), (О,6), (Р, 1), (Р, 2), (Р, 3), (Р, 4), (Р,5) и (Р,6). Один из возможных способов представить эти события—построить дерево подсчета, изображенное на рисунке:

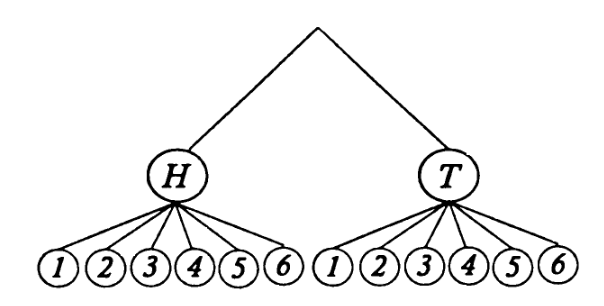
Очевидно, что таким образом представлены все исходы событий, и каждое из обведенных чисел изображает единственный исход. Если на монете выпал О, то существуют шесть возможных исходов для кубика; и те же шесть возможных исходов, если выпала "решка" Р. Таким образом, можно найти общее количество исходов, умножая 2x6, т.е. умножая число возможных исходов для подбрасывания монеты на число возможных исходов для подбрасывания игральной кости. Следует обратить внимание, что исход подбрасывания монеты не влияет на возможный исход подбрасывания кости.

Пример 1. Сколько существует различных инъективных отображений из множества A в множество B, если |A| = n, а |B| = m?

Решение.

Инъективное отображение подразумевает, что каждый элемент из области значения имеет единственный прообраз. Отметим сразу, что если a>b, такого отображения не существует.

Найдем число отображений по принципу умножения. Положим, что элементы множества A обозначены как . Образ для первого элемента a₁ можно выбрать m способами. Образ для элемента a₂ следует выбирать из множества , где f — отображение (а f(a₁) — образ элемента a₁), поскольку нельзя задействовать образ первого элемента. Таким образом, есть m-1 способов выбора образа элемента a₂. Рассуждая таким образом дальше, получаем, что образ элемента a₃ можно выбрать m-2 способами и т.д. В итоге число отображений по правилу умножения получается равным:

Предположим, что на собрании присутствуют 10 мужчин и 15 женщин, и кого-то одного нужно выбрать председателем. Существует 10+15=25 способов выбора председателя. Предположим, что человек направляется в ресторан, в котором предлагаются 15 блюд из говядины, 8 блюд из свинины и 12 блюд из морских продуктов. Посетителю ресторана предложен выбор из 15+8+12=35 различных блюд. Заметим, что в каждом случае множества, из элементов которых делается выбор, не пересекаются.

Комбинаторный принцип сложения. Пусть - попарно непересекающиеся множества, и пусть для каждого i множество S_i содержит n_i элементов. Количество вариантов выбора из S₁ или S₂ или … или S_m равно На языке теории множеств утверждение теоремы имеет вид:

Пример 2

Сколько нечетных целых чисел находятся между числами 100 и 1000?

Решение

Пусть S — множество нечетных целых чисел между 100 и 1000. Для пусть - подмножество множества S такое, что i является последней цифрой его элементов. Для каждого i существуют 9 вариантов выбора первой цифры и 10 вариантов выбора второй цифры, так что каждое множество S_i содержит 90 элементов. . поэтому между 100 и 1000 есть 450 нечетных чисел.

Рассмотрим теперь применение принципа сложения в том случае, когда множества могут пересекаться.

Пример 3. Чему равно , если множества S и T могут пересекаться?

Решение: (хорошо иллюстрировать на кругах Эйлера)

Представим как . Три слагаемых в последнем выражении, исходя из свойств операций над множествами, являются попарно непересекающимися, следовательно . Учтем также, что и , т.е. и . Следовательно,

Отсюда:

Для трех множеств формула будет такой:

Пример 4. Предположим, что, согласно исследованию, из 200 людей, смотрящих телевизор, 110 человек смотрят спортивную передачу, 120—комедии, 85 предпочитают драмы, 50 смотрят драмы и спорт, 70 — комедии и спорт, 55 смотрят комедии и драмы и 30 человек смотрят все три вида передач.

1. Сколько человек смотрят спорт, комедии или драмы?

2. Сколько человек не смотрят ничего из вышеперечисленного?

Пусть U —множество 200 людей, среди которых проводился опрос. Пусть S — множество людей, которые смотрят спорт; D —множество людей, которые смотрят драмы, и С — множество людей, предпочитающих комедии.

По приведенной выше формуле получаем, что

1.

2.

На диаграммах Эйлера эту задачу можно проиллюстрировать так. Известно, что 30 человек смотрят по телевидению спорт, комедии и драмы. Поскольку 50 человек смотрят спорт и драмы, то 20 человек должны смотреть спорт и драмы, но не смотреть комедии. Аналогично, 55 смотрят комедии и драмы, поэтому 25 человек должны смотреть комедии и драмы, но не смотреть спорт. К тому же 70 человек смотрят спорт и комедии, поэтому 40 из них смотрят спорт и комедии, но не смотрят драмы. Таким образом, получаем следующие диаграммы Эйлера (рис 8.6):

И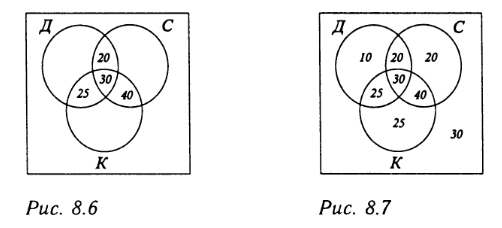 звестно, что 85 человек предпочитают смотреть драмы. Поскольку 75 из них уже перечислены, остальные 10 должны смотреть только драмы. Рассуждая аналогичным образом, получаем, что из 110 тех, кто смотрит спорт, уже перечислены 90 человек, поэтому оставшиеся 20 должны смотреть только спорт. И наконец, замечаем, что из 120 тех, кто смотрит комедии, 95 уже учтены. Таким образом, 25 человек смотрит только комедии. Если подсчитать количество людей в непересекающихся подмножествах, то получим число 170. Поэтому 30 человек не смотрят ни спорт, ни комедии, ни драмы (рис.8.7).

Задачи

1. Если компьютерный пароль содержит семь символов, которые могут быть цифрой или буквой английского алфавита, то сколько существует паролей, начинающихся с буквы?

В английском алфавите 26 букв. Считая строчные и прописные буквы разными, получаем 52 символа. Первый символ пароля может быть выбран 52 способами, остальные шесть — 62 способами (т.к. можно использовать цифры). Общее число комбинаций равно

2. Сколько существует способов избрания президента, вице-президента, секретаря и казначея среди членов клуба, включающего 8 студентов последнего курса, 10 студентов предпоследнего курса, 15 второкурсников и 20 первокурсников, если:

   1. отсутствуют какие-либо ограничения?

   2. президентом должен быть студент последнего курса?

   3. студент последнего курса не может быть вице-президентом?

   4. первокурсники могут быть избраны только на должность секретаря?

Всего имеем 8+10+15+20=53 члена клуба. В первом случае президента можно выбрать 53 способами, вице-президента — 52, секретаря — 51 и казначея — 50. В итоге способов.

Во втором случае есть 8 способов выбора президента. Тогда число комбинаций равно:

В третьем случае начнем выбор с вице-президента. Его можно выбрать 45 способами. В итоге число комбинаций рано

В последнем случае нужно рассмотреть два варианта:

• Секретарем выбирают первокурсника. Тогда секретаря можно выбрать 20 способами, президента — 33, вице-президента — 32, казначея — 31. Итого

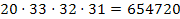
• Секретарем выбирают не первокурсника. Тогда первокурсники вообще в выборах не выбираются. Секретаря можно выбрать 33 способами, президента — 32, вице-президента — 31, казначея — 30, общее число способов равно 982090

Для получения общего числа способов для четвертого варианта сложим полученные количества. В итоге число комбинаций равно 1636800.

1. Сколько существует произвольных отображений из множества A в множество B, если |A| = n, а |B| = m? Сколько биективных отображений?

Поскольку для произвольного отображения единственным условием является наличие образа каждого элемента множества A, то общее число таких отображений может быть определено довольно просто. Т.к. для каждого элемента образ может быть выбран m способами, то общее число отображений будет равно

Биективное отображение можно построить только в том случае, когда m=n. В этом случае, используя решение из примера 1, получаем

2. Решить пример 2, пользуясь только принципом умножения.

3. С колько существует различных четырехзначных положительных чисел, если, по крайней мере, две цифры в числе совпадают? Числа, начинающиеся с нуля (например, 0001) не считаем четырехзначными.

Всего четырехзначных целых чисел существует 9000. Определим, сколько существует четырехзначных чисел с различными цифрами. Очевидно, первую цифру можно выбрать 9 способами. Вторую цифру — также 9 способами (т.к. появляется возможность выбрать 0), третью — 8 способами, четвертую — 7 способами. Если вычесть число четырехзначных чисел с разными цифрами из общего числа четырехзначных чисел, получим искомое число:

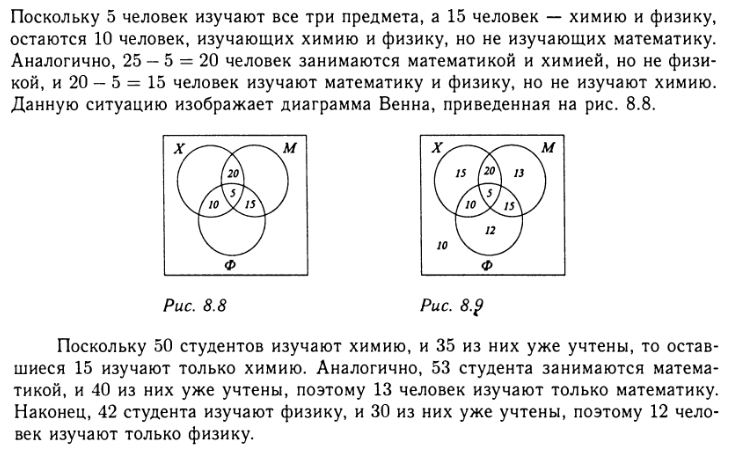
4. Предположим, что из 100 опрошенных студентов 50 изучают химию, 53 — математику, 42 — физику, 15 — химию и физику, 20 занимаются физикой и математикой, 25—математикой и химией и 5 студентов изучают все три предмета.

   1. Сколько студентов изучают хотя бы один из трех перечисленных предметов?

   2. Сколько студентов не изучают ни один из трех перечисленных предметов?

   3. Сколько студентов изучают только математику?

   4. Сколько студентов изучают физику или химию, но неизучают математику?

   5. Сколько студентов не изучают ни математику, ни химию?

Определения сочетаний, размещений и перестановок

//Перестановки

Переставляя объекты некоторого набора, мы обычно располагаем их в различном порядке. В этом смысле перестановка — это переупорядочение набора объектов. Для подсчета перестановок достаточно воспользоваться правилом умножения. Рассмотрим количество возможных способов формирования числа, переставляя цифры 1, 2, 3, 4 и 5. Варианты возможных перестановок — это, например, числа 12345, 15342, 32415 и 32415. Для нахождения количества возможных размещений или перестановок заметим, что первую цифру можно выбрать пятью способами, вторую — четырьмя способами, третью — тремя способами, четвертую — двумя, и только один вариант остается для выбора пятой цифры. Поэтому существует 5! возможных перестановок. Точно так же, если необходимо переупорядочить n объектов, то для этого существует n! способов. В перестановках важен порядок. Числа 51342 и 32415, образованные перестановкой цифр 1, 2, 3, 4 и 5, не совпадают. Кроме того, поскольку перестановки рассматриваются как переупорядочения, то каждый объект можно использовать только один раз.

Можно увидеть, что это равно числу биекций множества элементов на себя. Действительно, каждую перестановку можно интерпретировать как биективное отображение, устанавливающее связь между элементами до и после перестановки.

Итак, перестановка — это переупорядочение набора объектов, число перестановок n элементов вычисляется как n!.

//Размещения без повторений

Иногда бывает так, что объектов больше, чем мест их расположения. Предположим, например, что в организации — 20 человек и из них требуется выбрать президента, вице-президента, секретаря и казначея. Имеются 20 вариантов выбора президента, 19 вариантов выбора вице-президента, 18 способов выбора секретаря и 17 — казначея. Таким образом, получаем

способов выбора должностных лиц. Заметьте, что порядок все еще остается существенным. Есть разница, является ли Иванов президентом, вице-президентом, секретарем или казначеем. Каждое из размещений на должностях четырех выбранных лиц представляет собой различную организацию руководства, и любого человека можно избрать только один раз.

Комбинации такого вида, когда нас интересует и порядок элементов в комбинации и её состав, называются размещениями.

Предположим теперь, что имеется n человек. Требуется выбрать n из них и расположить в определенном порядке. Существует и способов выбрать первого человека, n - 1 способов выбора второго, n - 2 способов выбора третьего, n - j + 1 способов выбора j-ro и n - r + l способов выбора r-го человека. Следовательно, существует

способов выбрать г человек из n. Но

Следовательно число размещений n объектов по r местам вычисляется по n местам можно вычислить по формуле

//Сочетания без повторений

Теперь допустим, что в организации из 20 человек требуется выбрать не президента, вице-президента, секретаря и казначея, а просто комиссию из 4 человек. Теперь порядок больше не дает различий в способах выбора. При выборе четырех должностных лиц любая перестановка Иванов, Петров, Сидоров, Фёдоров была бы различной, но при избрании комитета они не различаются. Поскольку для каждых 4-х человек существует 4! перестановки четырех должностных лиц, которые не меняют состав комитета, для нахождения числа комитетов необходимо разделить на 4!. Комбинации такого вида, когда нас не интересует и порядок элементов в комбинации, а интересует только её состав, называются сочетаниями.

Теперь, рассуждая таким же образом, как и при решении данной задачи, получаем формулу для подсчёта числа сочетаний из n по r

Перестановки, размещения и сочетания с повторениями

До сих пор мы рассматривали случаи, когда все объекты были попарно различны. Если же часть предметов набора будут совпадать число перестановок, сочетаний и размещений будет вычисляться по-другому.

//Перестановки с повторениями.

Если некоторые из переставляемых предметов одинаковы, то суммарное число получается меньше, т. к. часть комбинаций совпадает друг с другом.

Например, требуется определить различные размещения букв в слове Миссисипи. Предположим сначала, что все буквы различны. В таком случае существовало бы 11! способов размещения 11 букв. Теперь обратим внимание, что буква "и" встречается четыре раза. Тогда все 11! комбинаций можно разбить на группы, элементы которых буду отличаться только расположением буквы «и» (наппр: «М и₁ с с и₂ с и₃ п и₄ », «М и₂ с с и₁ с и₃ п и₄ »...). В каждой группе будет по 4! комбинаций (по числу перестановок буквы и) . Сейчас они подсчитаны, как различные, хотя это не так. Значит каждым 4! комбинациям из 11! соответствует только одна перестановка. Тогда число перестановок, с учётом того, что все буквы «и» одинаковы будет 11!/4! . Размышляя аналогично относительно остальных повторяющихся букв (с — входит 3 раза — делить на 3!...), получаем

Рассмотрим общий случай. Пусть у нас есть объекты k различных типов и из них n1 объектов первого типа, n2 объектов второго типа … nk объектов типа №k. Рассуждая таким же образом, как и при решении предыдущей задачи задачи, получим формулу для подсчёта числа перестановок с повторениями.