Равномерное распределение

Непрерывная случайная величина называется равномерно распределенной на отрезке [a,b], если ее плотность распределения вероятностей на этом отрезке постоянна, а вне его равна 0, то есть имеет вид:

(с – соnst.)

Исходя из свойства функции плотности распределения, найдем значение константы с:

Откуда с = .

И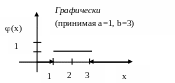 так, плотность вероятности непрерывной случайной величины Х, распределенной равномерно на отрезке [a, b], имеет вид:

Задача: Восстановить значение интегральной функции распределения в этом случае.

Решение: Проводя рассуждения, аналогичные тем, что применялись в примере 7 раздела 10.3, придем к следующему виду интегральной функции распределения:

Нормальное распределение

Непрерывная случайная величина нормально распределена, если ее плотность распределения имеет симметричный колоколообразный характер. Примеры подобных величин многочисленны и разнообразны:

масса клубня картофеля,

привес животного за месяц откорма,

рост (или вес) людей,

содержание жира в молоке,

погрешность измерения прибора.

На характер распределения упомянутых случайных величин влияет большое число факторов, причем влияние каждого из них относительно невелико и не является преобладающим над другими факторами.

Непрерывная случайная величина Х имеет нормальный закон распределения, если ее функция плотности вероятности имеет вид:

Здесь a=М(Х) – математическое ожидание или среднее значение,  = D(X) – среднее квадратическое отклонение случайной величины.

График плотности распределения

Исследование функции (х) при а=0 показывает:

1) Пересечение с осью OY в точке А(0, )

2) Экстремум:

Откуда х=0, то есть в точке А достигается максимум.

3) f(x)=0  ось ОХ – горизонтальная асимптота.

f(-x) = f(x)  функция четная (симметрична относительно оси OY).

4) Точки перегиба:

Откуда х=. Получаем две точки перегиба: ;

График функции f(х) представлен на рисунке 1.

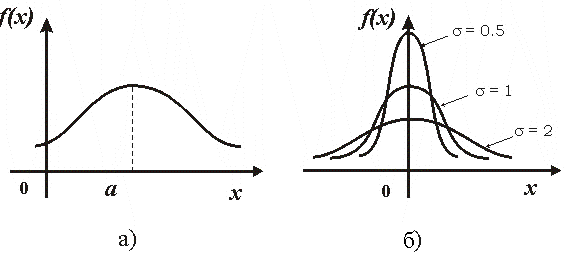
Рис.1:

а) общий вид функции плотности нормального распределения f(x);

б) зависимость f(x) от параметра при а = 0.

Как видно из рисунка 1, график функции y = f(x) имеет симметричный, колоколообразный характер, при меньшем значении  достигается меньшее рассеяние вокруг среднего и больший максимум; при a0 кривая плотности распределения сдвигается вправо на a единиц.

Вероятность попадания нормально распределенной случайной величины в заданный интервал.

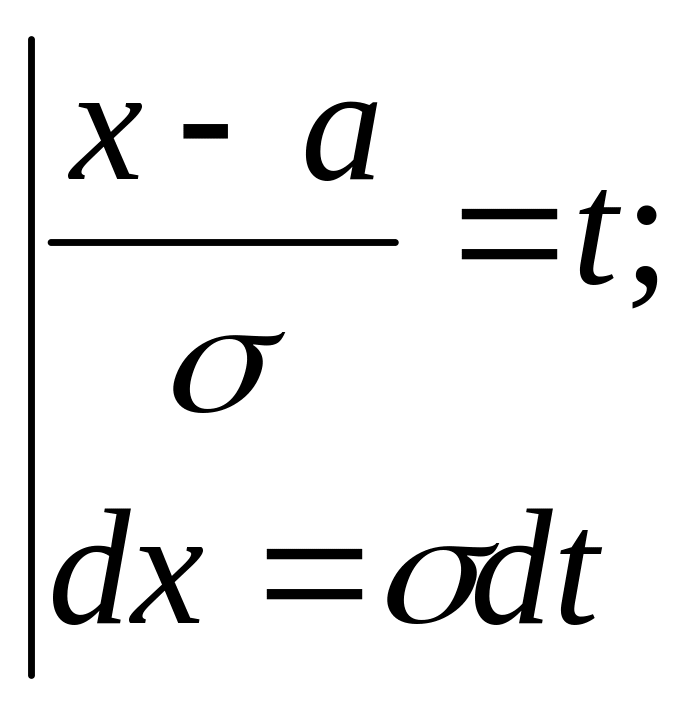
Где 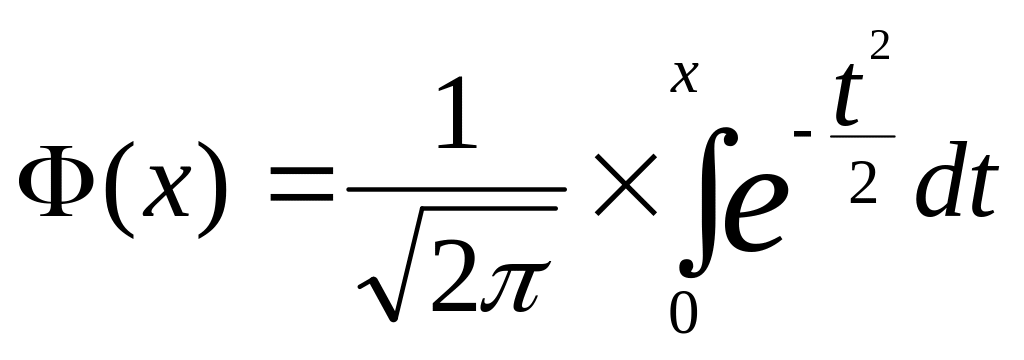- интегральная функция Лапласа, задается таблично.

Из свойств определенного интеграла Ф(-х)= - Ф(х), т.е. функция Ф(х) – нечетная.

Отсюда выводятся следующие (производные) формулы:

Полагая: а) =

(68%)

б) =2

(95%)

в) =3

(100%)

Правило трех сигм (3): практически достоверно, что при однократном испытании, отклонение нормально распределенной случайной величины от ее математического ожидания не превышает утроенного средне-квадратического отклонения.

Задача: Предполагается, что масса вылавливаемых в пруду зеркальных карпов есть случайная величина Х, имеющая нормальное распределение с математическим ожиданием a=375 г. и средним квадратическим отклонением  = 25 г. Требуется определить:

А) Вероятность, что масса случайно выловленного карпа окажется не менее =300 г. и не более =425 г.

Б) Вероятность, что отклонение указанной массы от среднего значения (математического ожидания) по абсолютной величине будет меньше = 40 г.

В) По правилу трех сигм найти минимальную и максимальную границы предполагаемой массы зеркальных карпов.

Решение:

А)

Вывод: Примерно 98% карпов, плавающих в пруду, имеют массу не менее 300 г. и не более 425 г.

Б)

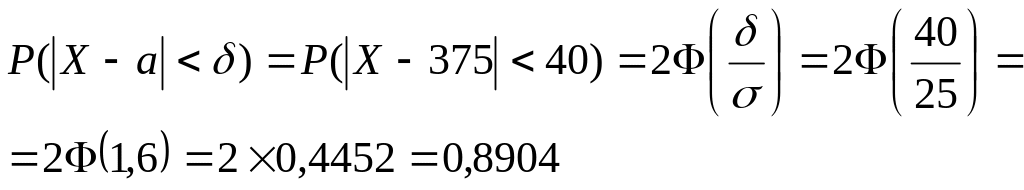
Вывод: Примерно 89% имеют массу от a- = 375- 40 = 335 г. до a+ = 375 + 40 = 415 г.

В) По правилу трех сигм:

Вывод: Масса практически всех карпов (примерно 100%) заключена в интервале от 300 до 450 грамм.