
- •Заняття 15 Модуль 5. Функції багатьох змінних
- •§5.1. Поняття функції багатьох змінних. Область її визначення. Графік та лінії рівнів.
- •§ 5.2. Границя та неперервність функції багатьох змінних.
- •Дослідити послідовність на збіжність:
- •Дослідити чи існує границя функції в точці :
- •Дослідити функцію на неперервність:
- •§ 5.3. Частинні похідні. Повний диференціал. Диференційовність функції двох змінних. Похідна за напрямом. Градієнт.
- •Заняття 16
- •§ 5.4. Екстремум функції двох змінних. Найбільше та найменше значення функції двох змінних в замкненій області
- •1. Дослідити на екстремум функції:
- •Знайти найбільше та найменше значення функції в замкненій області , якщо:
Заняття 16
§ 5.4. Екстремум функції двох змінних. Найбільше та найменше значення функції двох змінних в замкненій області
Точка
![]() називається точкою
локального мінімуму функції
називається точкою
локального мінімуму функції
![]() ,
якщо існує окіл точки
,
якщо існує окіл точки
![]() такий, що для всіх точок
такий, що для всіх точок
![]() з цього околу виконується умова
з цього околу виконується умова
![]() .
.
Точка
називається точкою
локального максимуму функції
,
якщо існує окіл точки
такий, що для всіх точок
з цього околу виконується умова
![]() .
.
Точка, в якій всі частинні похідні перетворюються в нуль, називається стаціонарною точкою.
Теорема
(необхідна умова екстремуму). Якщо
-
точка екстремуму диференційовної
функції
![]() ,
то в цій точці виконуються умови :
,
то в цій точці виконуються умови :
![]()
Теорема
(достатня умова екстремуму). Нехай
— стаціонарна точка функції
![]() ,
причому в околі точки
існують неперервні частинні похідні
другого порядку цієї функції і
,
причому в околі точки
існують неперервні частинні похідні
другого порядку цієї функції і
![]() .
.
І. Якщо
![]() ,
то функція
в точці
має екстремум:
,
то функція
в точці
має екстремум:
а) якщо
![]() ,
то
— точка мінімуму;
,
то
— точка мінімуму;
б) якщо
![]() ,
то
— точка максимуму.
,
то
— точка максимуму.
ІІ. Якщо
![]() ,
то точка
не є точкою екстремуму функції
.
,
то точка
не є точкою екстремуму функції
.
ІІІ.
Якщо
![]() ,
то потрібне додаткове дослідження.
,
то потрібне додаткове дослідження.
Дві останні теореми вказують алгоритм дослідження диференційовної функції двох змінних на екстремум:
1 крок. Знайти стаціонарні точки, як розв'язки системи
![]()
2 крок. У всіх стаціонарних точках перевірити виконання достатніх умов екстремуму.
Нехай
![]() —
замкнена область,
—
замкнена область,
![]() ,
— диференційовна (а отже і неперервна)
функція. Тоді за теоремою Вейєрштрасса
функція
приймає в області
своє найбільше та найменше значення.
Точки, в яких функція набуває екстремальних
значень, можуть бути як внутрішніми
точками цієї області (в цьому випадку
це будуть точки локального екстремуму),
так і межовими точками.
,
— диференційовна (а отже і неперервна)
функція. Тоді за теоремою Вейєрштрасса
функція
приймає в області
своє найбільше та найменше значення.
Точки, в яких функція набуває екстремальних
значень, можуть бути як внутрішніми
точками цієї області (в цьому випадку
це будуть точки локального екстремуму),
так і межовими точками.
Тому дослідження диференційовної функції на найбільше (найменше) значення функції в замкненій області доцільно проводити за наступним планом:
Знайти стаціонарні точки і обчислити значення функції в стаціонарних точках, які належать області (при цьому не обов’язково визначати, чи є стаціонарні точки точками екстремуму).
Дослідити функцію на найбільше (найменше) значення на межі
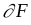 .
.Серед знайдених значень функції вибрати найбільше та найменше.
Приклади.
1. Дослідити на екстремум функції:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
Розв’язання. а) Знайдемо стаціонарні точки із системи:
![]()
![]()
![]()
![]() –– стаціонарна
точка.
–– стаціонарна
точка.
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
.
![]() .
Отже, точка
не є точкою екстремуму.
.
Отже, точка
не є точкою екстремуму.
б) Знайдемо стаціонарні точки з системи:
![]()
![]()
Отже,
![]() –– стаціонарна точка.
–– стаціонарна точка.
,
![]() ;
;
,
![]() ;
;
![]() ,
,
![]() .
.
![]() .
Отже,
–– точка екстремуму. Оскільки
.
Отже,
–– точка екстремуму. Оскільки
![]() ,
то
–– точка локального мінімуму.
,
то
–– точка локального мінімуму.
в) Знайдемо стаціонарні точки:
![]()
![]()
![]() –– стаціонарна
точка.
–– стаціонарна
точка.
![]() ,
,
![]() ;
;
,
![]() ;
;
![]() ,
,
![]() .
.
![]() .
.
Вищевказана теорема не дає відповіді на питання чи є точка точкою екстремуму. Але легко бачити, що в довільному околі точки є точки, в яких функція набуває додатних значень (це довільні точки з І чверті) і точки, в яких функція набуває від’ємних значень (це довільні точки з ІІІ чверті). Отже, точка не є точкою екстремуму.
