1.3.Метод Наименьших Квадратов.

Метод наименьших квадратов (МНК) – самый известный моделирования метод параметрической идентификации. Схема его применения сводится к трём основным этапам:

1) решение задачи структурной идентификации;

2) постановка задачи выпуклой оптимизации;

3) формирование и решение системы нормальных уравнений.

Пусть регрессионная модель объекта будет иметь вид линейной зависимости:

. (3.1)

Чтобы получить оценки коэффициентов этой модели, формируют алгоритм, удовлетворяющий критерию НК:

. (3.2)

С этой целью, из необходимого условия экстремума

, (3.3)

получается система нормальных уравнений ( линейного алгебраического уравнения с неизвестными):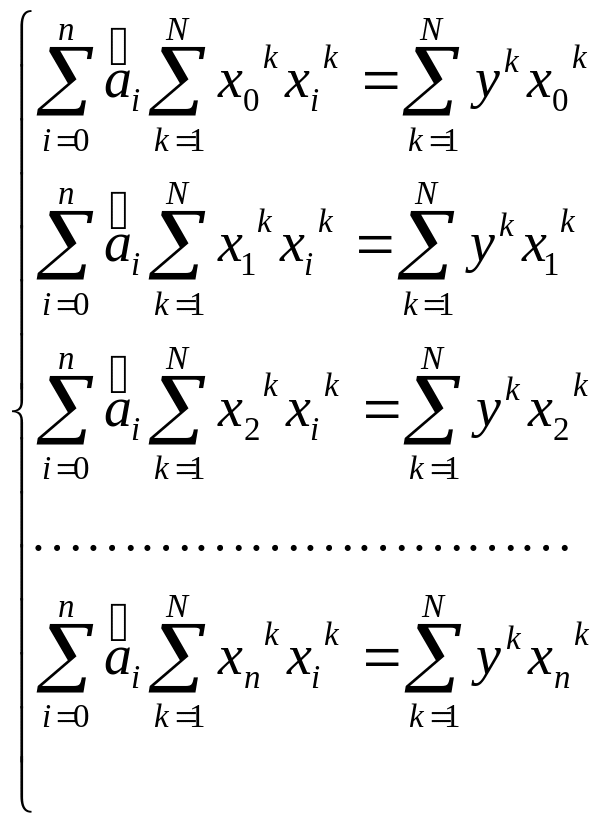 (3.4)

Эту систему неоднородных линейных уравнений следует решить любым из известных методов в высшей алгебре, например, методом Крамера, Гаусса, обратной матрицы и т.п., предварительно проверив матрицу коэффициентов этой системы на невырожденность.

Проводится проверка значимости коэффициентов по t - критерию Стьюдента. Оценки дисперсии и коэффициентов вычисляются по формулам:

(3.5)

(3.6)

(3.7)

Проверка адекватности модели проводится известным методом Фишера.

Рототабельные планы нашли широкое применение на практике. Однако с точки зрения математиков, занимающихся развитием математической статистики, выбор такого критерия представляется мало обоснованным. Он не вытекает логически из тех идей, на которые базируется математика. Например, как выбрать расстояние  до звездных точек; не все пространства независимых переменных, отведенное для эксперимента, используется в композиционных планах и т.д. Невозможно из множества рототабельных планов при одном и том же числе факторов выбрать лучший, т.к. не было критерия оценки. Поэтому этот критерий стали относить к эмпирико-интуитивным критериям.

Наряду с развитием планирования экспериментов, основанных на эмпирико-интуитивным критериях Бокса в США стало развиваться второе чисто теоретическое направление, которое связывают с планом ученого Кифера. Он установил связь между некоторыми критериями оптимальности; теоретически доказал, что для отдельных видов регрессии одни и те же планы могут отвечать сразу нескольким критериям оптимальности.

Взвешенный метод наименьших квадратов.

Далеко не все задачи исследования взаимосвязей экономических переменных описываются обычной линейной регрессионной моделью. Во-первых, исходные данные могут не соответствовать тем или иным предпосылкам линейной регрессионной модели и требовать либо дополнительной обработки, либо иного модельного инструментария. Во-вторых, исследуемый процесс во многих случаях описывается не одним уравнением, а системой, где одни и те же переменные могут быть в одних случаях объясняющими, а в других - зависимыми. В-третьих, исследуемые взаимосвязи могут быть (и обычно являются) нелинейными, а процедура линеаризации не всегда легко осуществима и может приводить к искажениям. В-четвертых, структура описываемого процесса может обусловливать наличие различного рода связей между оцениваемыми коэффициентами регрессии, что также предполагает необходимость использования специальных методов.

Наиболее распространенным в практике статистического оценивания параметров уравнений регрессии является метод наименьших квадратов. Этот метод основан на ряде предпосылок относительно природы данных и результатов построения модели. Основные из них - это четкое разделение исходных переменных на зависимые и независимые, некоррелированность факторов, входящих в уравнения, линейность связи, отсутствие автокорреляции остатков, равенство их математических ожиданий нулю и постоянная дисперсия. Эмпирические данные не всегда обладают такими характеристиками, т.е. предпосылки МНК нарушаются. Применение этого метода в чистом виде может привести к таким нежелательным результатам, как смещение оцениваемых параметров, снижение их состоятельности, устойчивости, а в некоторых случаях может и вовсе не дать решения. Для смягчения нежелательных эффектов при построении регрессионных уравнений, повышения адекватности моделей существует ряд усовершенствований МНК, которые применяются для данных нестандартной природы.

Одной из основных гипотез МНК является предположение о равенстве дисперсий отклонений еi, т.е. их разброс вокруг среднего (нулевого) значения ряда должен быть величиной стабильной. Это свойство называется гомоскедастичностью. На практике дисперсии отклонений достаточно часто неодинаковы, то есть наблюдается гетероскедастичность. Это может быть следствием разных причин. Например, возможны ошибки в исходных данных. Случайные неточности в исходной информации, такие как ошибки в порядке чисел, могут оказать ощутимое влияние на результаты. Часто больший разброс отклонений єi, наблюдается при больших значениях зависимой переменной (переменных). Если в данных содержится значительная ошибка, то, естественно, большим будет и отклонение модельного значения, рассчитанного по ошибочным данным. Для того, чтобы избавиться от этой ошибки нам нужно уменьшить вклад этих данных в результаты расчетов, задать для них меньший вес, чем для всех остальных. Эта идея реализована во взвешенном МНК.

Пусть на первом этапе оценена линейная регрессионная модель с помощью обычного МНК. Предположим, что остатки еi независимы между собой, но имеют разные дисперсии (поскольку теоретические отклонения еi нельзя рассчитать, их обычно заменяют на фактические отклонения зависимой переменной от линии регрессии ^., для которых формулируются те же исходные требования, что и для єi). В этом случае квадратную матрицу ковариаций cov(ei, ej) можно представить в виде:

(3.8)

где cov(ei, ej)=0 при i  j; cov(ei, ej)=S2; п - длина рассматриваемого временного ряда.

Если величины известны, то далее можно применить взвешенный МНК, используя в качестве весов величины и минимизируя сумму

(3.9)

Формула Q, записана для парной регрессии; аналогичный вид она имеет и для множественной линейной регрессии. При использовании IVLS оценки параметров не только получаются несмещенными (они будут таковыми и для обычного МНК), но и более точными (имеют меньшую дисперсию), чем не взвешенные оценки.

Проблема заключается в том, чтобы оценить величины s2, поскольку заранее они обычно неизвестны. Поэтому, используя на первом этапе обычный МНК, нужно попробовать выяснить причину и характер различий дисперсий еi. Для экономических данных, например, величина средней ошибки может быть пропорциональна абсолютному значению независимой переменной. Это можно проверить статистически и включить в расчет МНК веса, равные .

Существуют специальные критерии и процедуры проверки равенства дисперсий отклонений. Например, можно рассмотреть частное от деления cумм самых больших и самых маленьких квадратов отклонений, которое должно иметь распределение Фишера в случае гомоскедастичности.

Использование взвешенного метода в статистических пакетах, где предоставлена возможность задавать веса вручную, позволяет регулировать вклад тех или иных данных в результаты построения моделей. Это необходимо в тех случаях, когда мы априорно знаем о не типичности какой-то части информации, т.е. на зависимую переменную оказывали влияние факторы, заведомо не включаемые в модель. В качестве примера такой ситуации можно привести случаи стихийных бедствий, засух. При анализе макроэкономических показателей (ВНП и др.) данные за эти годы будут не совсем типичными. В такой ситуации нужно попытаться исключить влияние этой части информации заданием весов. В разных статистических пакетах приводится возможный набор весов. Обычно это числа от О до 100. По умолчанию все данные учитываются с единичными весами. При указании веса меньше 1 мы снижаем вклад этих данных, а если задать вес больше единицы, то вклад этой части информации увеличится. Путем задания весового вектора мы можем не только уменьшить влияние каких - либо лет из набора данных, но и вовсе исключить его из анализа. Итак, ключевым моментом при применении этого метода является выбор весов. В первом приближении веса могут устанавливаться пропорционально ошибкам не взвешенной регрессии.[2]

Аппроксимация (от латинского "approximate" -"приближаться")- приближенное выражение каких-либо математических объектов (например, чисел или функций) через другие более простые, более удобные в пользовании или просто более известные. В научных исследованиях аппроксимация применяется для описания, анализа, обобщения и дальнейшего использования эмпирических результатов.

Как известно, между величинами может существовать точная (функциональная) связь, когда одному значению аргумента соответствует одно определенное значение.

При выборе аппроксимации следует исходить из конкретной задачи исследования. Обычно, чем более простое уравнение используется для аппроксимации, тем более приблизительно получаемое описание зависимости. Поэтому важно считывать, насколько существенны и чем обусловлены отклонения конкретных значений от получаемого тренда. При описании зависимости эмпирически определенных значений можно добиться и гораздо большей точности, используя какое-либо более сложное, многопараметрическое уравнение. Однако нет никакого смысла стремиться с максимальной точностью передать случайные отклонения величин в конкретных рядах эмпирических данных. Выбирая метод аппроксимации, исследователь всегда идет на компромисс: решает, в какой степени в данном случае целесообразно и уместно «пожертвовать» деталями и, соответственно, насколько обобщенно следует выразить зависимость сопоставляемых переменных. Наряду с выявлением закономерностей замаскированных случайными отклонениями эмпирических данных от общей закономерности, аппроксимация позволяет также решать много других важных задач: формализовать найденную зависимость; найти неизвестные значения зависимой переменной путем интерполяции или, если это допустимо, экстраполяции.

точечной аппроксимации - одним из основных типов точечной аппроксимации является интерполирование. Оно состоит в следующем: для данной функции y=f(x) строим многочлен (2.1), принимающий в заданных точках x_i те же значения y_i, что и функция f(x), т.е. g(x_i)=y_i, i=0,1,…n.

При этом предполагается, что среди значений x_i нет одинаковых, т.е. x_ix_k при этом ik. Точки x_i называются узлами интерполяции, а многочлен g(x) - интерполяционным многочленом.

Y

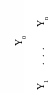
X

X₀ X₁ . . . X_n

Рис. 4

Таким образом, близость интерполяционного многочлена к заданной функции состоит в том, что их значения совпадают на заданной схеме точек (рис.4, сплошная линия).

Максимальная степень интерполяционного многочлена m=n; в этом случае говорят о глобальной интерполяции.

При большом количестве узлов интерполяции получается высокая степень многочлена в случае глобальной интерполяции, т.е. когда нужно уметь один интерполяционный многочлен для всего интервала изменения аргумента. Кроме того, табличные данные могли быть получены путем измерений и содержать ошибки. Построение аппроксимируемого многочлена с условием обязательного прохождения его графика через эти экспериментальные точки означало бы тщательное повторение допущенных при измерениях ошибок. Выход из этого положения может быть найден выбором такого многочлена, график которого проходит близко от данных точек (рис.1, штриховая линия).

Одним из таких видов является среднеквадратичное приближение функции с помощью многочлена. При этом m  n; случай m = n соответствует интерполяции. На практике стараются подобрать аппроксимирующий многочлен как можно меньшей степени (как правило, m=1, 2, 3).

Мерой отклонения многочлена g(x) от заданной функции f(x) на множестве точек (x_i,y_i) (i=0,1,…,n) при среднеквадратичном приближении является величина S, равная сумме квадратов разности между значениями многочлена и функции в данных точках:

_n

S = [g(x_i)-y_i]²

ⁱ⁼⁰

Для построения аппроксимирующего многочлена нужно подобрать коэффициенты a₀, a₁,…,a_m так, чтобы величина S была наименьшей. В этом состоит метод наименьших квадратов.[3]

1.4.Постановка задачи.

Создание модели оценки стоимостных характеристик объектов жилого фонда для повышения эффективности риэлтерской недвижимостью.

2.Разработка программного продукта.

2.1.Алгоритм.

2.2.Описания алгоритма.

2.3.Выбор языка программирования.

C++ Bulder 6 система объектно-ориентированного программирования производства корпорации Borland предназначена для операционных систем Windows 95 и Windows 7. Интегрированная среда C++ Builder обеспечивает скорость визуальной разработки, продуктивность повторно используемых компонент в сочетании с мощью языковых средств C++, усовершенствованными инструментами и разномасштабными средствами доступа к базам данных.

C++ Builder может быть использован везде, где требуется дополнить существующие приложения расширенным стандартом языка C++, повысить быстродействие и придаст пользовательскому интерфейсу качества профессионального уровня

.