Часть . Случайные события. Вероятность.

.1. Основные определения

Основным понятием теории вероятностей является опыт  совокупность условий, который может быть воспроизведен сколько угодно раз, и результаты опыта, называемые событиями. Обозначаются события большими буквами латинского алфавита  .

Событие, которое в результате опыта происходит всегда, называется достоверным, обозначается . Событие, которое в результате опыта не происходит никогда, называется невозможным, обозначается .

Над событиями определены отношения включения: ( ) и эквивалентности: (~). Так, означает, что если происходит событие , то происходит и событие .

~ означает, что и . Обозначают эквивалентные события = .

Очевидно, что для любого события справедливы соотношения: .

Над событиями определяются операции объединения (суммы), пересечения (произведения), разности и отрицания.

1. Суммой (или объединением событий называется событие , состоящее в том, что в опыте происходит хотя бы одно из событий . Для записи суммы событий используется одно из обозначений

.

2. Произведением (или объединением) событий называется событие , состоящее в том, что в опыте происходят все события . Для обозначения произведения событий используются обозначения

3. Разностью событий и называется событие, состоящее в том, что событие происходит, а событие не происходит.

4. Отрицанием события называется событие , состоящее в том, что событие не происходит. Очевидно, что = .

Введем ряд важных для дальнейшего определений.

1. События называются единственно возможными, если хотя бы одно из них происходит в результате опыта, т. е. их объединение является достоверным событием:

2. События называются попарно несовместными, если пересечения различных пар событий являются невозможным событием

;

3. События образуют полную группу событий, если они попарно несовместны и единственно возможны.

Например, события и образуют полную группу.

К основным понятиям теории вероятностей относятся также частота и вероятность события. Относительной частотой (или просто частотой) события называется отношение числа опытов , в которых появилось событие , к общему числу опытов :

Свойства частоты:

1.

2.

3. Для любых несовместных событий и , связанных с данным опытом, справедливо соотношение

В теории вероятностей изучаются случайные явления, в которых частоты событий обладают свойством устойчивости: при увеличении числа испытаний частота события колеблется около некоторого числа , называемого вероятностью события:

.

Это статистическое определение вероятности. Его недостаток в том, что оно не дает однозначного значения вероятности события. Существует несколько определений вероятности событий. Наиболее полным является аксиоматическое определение вероятности, введенное Колмогоровым в 1933г. Оно повторяет свойства частоты событий. Из него следуют свойства вероятностей, которыми мы в дальнейшем будем пользоваться:

1. Вероятность невозможного события ;

2. Вероятность противоположного события ;

3. Для любого события справедливы неравенства ;

4. Если , то ;

5. Для попарно несовместных событий справедлива теорема сложения вероятностей

.

.2. Классический подход к вычислению вероятностей

Этот подход имеет место, когда число простейших исходов опыта конечно и эти исходы равновозможны.

Тогда вероятность события определяется по формуле

(.1)

где число исходов опыта, благоприятствующих событию , общее число равновозможных исходов.

Формула (.1) называется классической формулой вероятности.

При использовании классической формулы вероятности полезны формулы комбинаторики. Рассмотрим некоторые из них.

Размещения.

Пусть имеется множество из элементов. Каждое его упорядоченное подмножество из элементов называется размещением из элементов по , обозначается . Итак, размещения – это подмножества из элементов, отличающиеся друг от друга либо элементами, либо порядком элементов. Число размещений находится по формуле

, (.2)

где (читается «эн факториал») – это произведение натуральных чисел от 1 до : . Очевидно, , принято .

Перестановки.

При значении размещения называют перестановками из элементов:

(.3)

Перестановки отличаются друг от друга только порядком элементов.

Сочетания.

Любые подмножества из элементов некоторого множества из элементов называются сочетаниями из элементов по , обозначается . Сочетания отличаются друг от друга только элементами. Число сочетаний находится по формуле

(.4)

Очевидно, .

Правило произведений.

Правило произведений в общем случае формулируется так: если элемент можно выбрать способами, элемент – способами и т.д., элемент – способами, то комбинацию элементов можно выбрать способами.

.3. Условные вероятности. Теорема умножения вероятностей

Условная вероятность события при условии, что произошло событие , определяется по формуле

(.5)

Аналогично условная вероятность события при условии, что событие произошло, определяется по формуле

(.6)

Из формул (.5) и (.6) получаем теорему умножения вероятностей

(.7)

Теорема умножения вероятностей обобщается на случай сомножителей:

(.8)

.4. Попарная независимость событий. Независимость в совокупности

Введем определения.

1. События и называются независимыми, если выполняется условие

(.9)

Из формул (.5) получаем, что для независимых событий и условные вероятности равны безусловным вероятностям:

.

2. События называются попарно независимыми, если для любых двух событий из них выполняются условия

.

3. События называются независимыми в совокупности, если для любых = 1, 2, . . . , и выполняется условие

.

Теорема умножения вероятностей (.8) для независимых в совокупности событий примет вид:

.5. Теорема сложения вероятностей

Если события , совместны ( Ø), то вероятность объединения этих событий определяется по формуле

(.10)

Формула (.10) называется теоремой сложения вероятностей совместных событий.

Если события , несовместны ( Ø) , то из формулы (.10) получаем теорему сложения вероятностей несовместных событий

.

.6. Надежность элементов и систем

Надежностью элемента (системы) называется вероятность безотказной работы системы в течение некоторого промежутка времени [0,T]. Расчет надежности системы зависит от структуры системы, определяемой схемой расположения составляющих ее элементов. Рассмотрим два простейших случая расположения элементов системы.

1) элементов системы (1), (2), . . ., ( ) объединены в системе последовательно, если (по аналогии с электрической цепью) система безотказно работает, когда работают все ее элементы. Отказ такой системы происходит тогда и только тогда, когда отказывает хотя бы один элемент системы.

Пусть – событие, состоящее в том, что – ый элемент системы работает безотказно в течение времени . Тогда – событие – – ый элемент системы отказывает в течение времени . Вероятности этих событий связаны соотношением: . Событие (система из последовательно соединенных элементов работает в течение промежутка времени ) определяется как

Если элементы системы работают независимо друг от друга (события независимы в совокупности), то надежность системы определяется по формуле

(.11)

2) элементов системы (1), (2), . . ., ( ) объединены в системе параллельно, если в течение времени система откажет тогда и только тогда, когда откажут все ее элементов. Работу такой системы обеспечивает хотя бы один работающий элемент. Событие (система из параллельно соединенных элементов работает в течение промежутка времени ) определяется как

. (.12)

Событие – отказ системы в течение времени определяется как

. Надежность системы . Если события независимы в совокупности, то надежность системы определится формулой

(.13)

.7. Формула полной вероятности. Формулы Байеса

Пусть события образуют полную группу событий, т.е.

1) события попарно несовместны ( Ø, ),

2) события единственно возможны, т.е. .

Тогда вероятность любого события , происходящего в условиях эксперимента, определяется по формуле

(.14)

Формула (.14) называется формулой полной вероятности.

Если известно, что в условиях эксперимента некоторое событие произошло, то условные вероятности событий , определяются по формулам

. (.15)

Формулы (.15) называются формулами Байеса или формулами вероятностей гипотез.

.8. Схема Бернулли

Схемой Бернулли называется последовательность независимых испытаний с двумя исходами и в каждом испытании. Вероятности не зависит от номера испытания. Обозначим – число появлений события в испытаниях Бернулли.

Основные задачи на схему Бернулли.

1. Вероятность того, что событие в испытаниях Бернулли появилось раз определяется формулой

. (.16)

2. Вероятность того, что событие в испытаниях Бернулли появилось не менее раз, но не более раза, определяется формулой

. (.17)

3.Наивероятнейшее число появления события в испытаниях Бернулли определяется из двойного неравенства

(.18)

.9. Локальная и интегральная формулы Муавра  Лапласа.

Вычисления по формуле (.16) для больших значений практически невозможны. Используются различные приближенные формулы. Так для вероятностей , близких к 0,5, больших значений используется локальная формула Муавра – Лапласа:

, (.19)

где – параметры схемы Бернулли.

Функция называется локальной функцией Лапласа.

Свойства функции : 1) ; 2)

Формула (.19) дает большую погрешность для вероятностей, близких к нулю и единице.

При больших значениях формула (.17) непригодна для вычислений. Используется интегральная формула Муавра – Лапласа, согласно которой

,где (.20) . (.21)

Функция называется стандартной интегральной функцией Лапласа.

Свойства функции : 1) ;

2) .

Для функций , составлены таблицы (приложения 1, 2).

Интегральная формула Лапласа (.17) позволяет оценить вероятность отклонения частоты события от вероятности этого события :

(.22)

.10. Формула Пуассона.

Для больших , малых вероятностей когда , применяется формула Пуассона

(.23)

Число называется параметром Пуассона.

.11. Примеры расчета.

Задача .1.На рисунке 1 представлена система из шести независимо работающих элементов. Обозначим событие, состоящее в том, что элемент « » работает. Используя операции алгебры событий, выразить через события событие состоящее в том, что система из шести элементов работает, Найти надежность системы, если надежности элементов:

Решение.

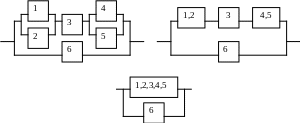
Рис.1. Рис.2.

Рис. 3.

Элементы (1) и (2), а также (4) и (5) соединены параллельно. События и , состоящие в том, что блоки (1,2) и (4,5) работают, согласно п. .6 имеют вид: и

Заменяем их элементами (1,2) и (4,5) с надежностями и , соответственно (формула .13) .

Вместо исходной системы рассматриваем эквивалентную ей систему элементов (1,2), (3), (4,5) и (6), соединенных по схеме на рис.2.

Элементы (1,2), (3) и (4,5) соединены последовательно. Заменяем их элементом (1,2,3,4,5). Событие, состоящее в том, что этот элемент системы работает, имеет вид: . Надежность элемента (1,2,3,4,5) равна

.

Таким образом, вместо исходной системы мы можем рассматривать систему из двух параллельно соединенных элементов (1,2,3,4,5) и (6) с надежностями и , соответственно (рис. 3).

Надежность этой системы

Подставляя заданные надежности элементов, последовательно вычисляем

Ответ: 0,87831.

Задача .2. Из набора карт в 52 листа наудачу извлекают 4 карты. Найти вероятность того, что среди них 3 короля (событие ).