§5. Интегрирование рациональных выражений

1. Основные понятия

Определение. Рациональной функцией (или рациональной дробью) называется функция вида = , где P_n, Q_m – многочлены степеней n и m соответственно. Если n<m, то рациональная дробь называется правильной, в противном случае (n≥m) – неправильной.

Если рациональная дробь неправильная, то её с помощью деления можно представить в виде суммы многочлена (целая часть) и правильной рациональной дроби, т.е. = + , где P_n-m(x) – многочлен степени n – m, r <m .

Примеры.

1) Метод деления

4 x⁴– 3x³+ x² – 1 x² - 3x+ 1

4 x⁴–12x³+4x² 4x² +9x+24

9x³ – 3x² - 1

9x³–27x² + 9x

24x² – 9x – 1

24x²–72x + 24

63x – 25

2) Метод преобразований

.

2. Интегрирование простейших дробей.

Определение. Простейшими дробями называются дроби следующих четырёх типов:

1) ; 2) ; 3) ; 4) ,

где A, M, N, a, p, q , трехчлен не имеет действительных корней (т. е. D=p²–4q<0).

1) ;

2) ;

3) .

В числителе выделяется выражение равное производной знаменателя. Разделив затем почленно, получим табличный интеграл и интеграл вида

, который вычисляется путём выделения полного квадрата в знаменателе.

Пример.

.

4) 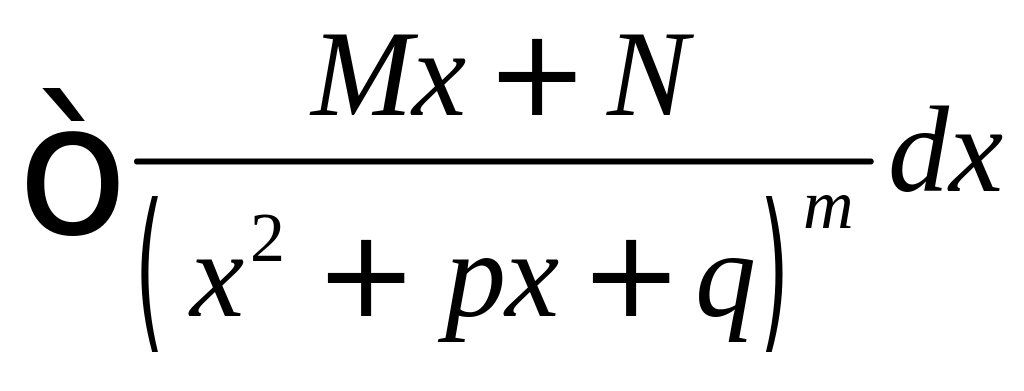вычисляется аналогично интегралу вида 3) с применением рекуррентной формулы (7).

3. Разложение правильной рациональной дроби на сумму простейших

Пусть - правильная рациональная дробь, Q(x) – многочлен степени n с коэффициентом перед старшей неизвестной равным единице (для простоты): Q(x)=xⁿ+b₁x^n-1+…+b_n. Q(x) имеет n действительных и комплексных корней. Так как у Q(x) коэффициенты – действительные числа, то комплексные корни попарно сопряжены.

Если a₁, a₂, … a_n – действительные корни Q(x), то Q(x)=(x–a₁)(x–a₂)… (x-a_n).

Может быть, что a₁=a₂=…=a_k=a, тогда Q(x)=(x-a)^k(x-a_k+1)… (x-a_n), т.е. если а – корень крайности к, то в разложении присутствует множитель (x-a)^k.

Если l+ki и l–ki – сопряжённые комплексные корни, то

(x-(l+ki))(x-(l-ki))=((x-l)+ki)((x-l)-ki)=(x-l)²-(ki)²=x²-2lx+l²+k²=x²+px+q,

. Следовательно, сопряжённым комплексным корням соответствует в разложении Q(x) квадратный трёхчлен с действительными коэффициентами.

Если l+ki и l–ki – корни кратности m, то в разложении Q(x) будет присутствовать множитель (x²+px+q)^m.

Теорема 1. Если Q(x) – многочлен степени n с действительными коэффициентами, то его можно единственным образом разложить на линейные и квадратичные множители с действительными коэффициентами.

Если a₁, a₂, …, a_n – действительные корни кратности m₁, m₂, …, m_r соответственно, – комплексные корни кратности μ₁, μ₂, …, μ_s соответственно, то разложение Q(x) на неприводимые множители имеет вид:

(1),

где .

Теорема 2. Если - правильная рациональная дробь, а разложение Q(x) на неприводимые множители имеет вид (1), то справедливо разложение:

. (2)

Теорема 2 утверждает, что любую рациональную дробь можно представить в виде суммы конечного числа простейших дробей.

Вычисление коэффициентов разложения

I. Метод неопределённых коэффициентов

По виду многочленов знаменателя правильной рациональной дроби пишут для этой дроби разложение (2) с буквенными коэффициентами. Затем в правой части разложения дроби приводят к общему знаменателю. В результате получают две тождественно равные дроби с одинаковыми знаменателями. Приравнивают числители:

P(x)=c₁x^n-1+c₂x^n-2+…+c_n-1х+c_n. (3)

Приравнивая коэффициенты при равных степенях x, получают систему из n линейных уравнений с n неизвестными c₁, c₂,…, c_n. Решая её, находят c₁, c₂,…, c_n и подставляют в разложение (2). В силу теоремы 2 это разложение единственно.

Пример. .

;

.

 

Тогда

II. Метод произвольных значений

В тождестве (3) переменной х придают n произвольных значений и получают n уравнений с n неизвестными c₁, …, c_n. В качестве значений х удобно брать значения, равные действительным корням.

Пример. .

Тогда .