ЛЕКЦИИ
ПО УМФ(2 СЕМЕСТР)
Задачи для уравнения тепловодности. Принцип максимума.
Процесс распространения тепла в объеме с плотностью , коэффициентом теплопроводности с.
Если среда однородна, изотропна, , с, k – const, то
Будем рассматривать область D R3, D=S, 0<t≤T>0, QT – цилиндр, в основании которого лежит D, направляющие параллельны оси t.
t
y
D
x S
Часть общей
поверхности цилиндра
Рассмотрим в QT следующую задачу: найти решение уравнения (1).
(M,t)QT,
непрерывные вплоть до границы такое,
что
должны выполняться
условия согласования:
Теорема. Принцип максимума.
Решение задачи (1),(2),(3) в цилиндре QT , непрерывные вплоть до границы области, достигает своего наибольшего и наименьшего значения на ГТ.
min u(M, t) ≤ max u(M, t) ≤ max u(M, t)
(M, t)ГT (M, t)QT (M, t)ГT
Доказательство: (от противного).
Обозначим через m = max u(M, t) , max u(M, t) = M
(M, t)ГT QT/ГТ
Предположим M > m. Таким образом u(M0, t0) = M, M0 D, Q< t0≤ T.
Введем вспомогательную функцию:
,
где d
– диаметр D
Оценим значение V во внутренних точках и на границе:
ГТ
:
V(M0, t0) = M, следовательно V не принимает наибольшего значения на ГТ, а в
какой-то внутренней точке.
max V(M, t) = V(M1, t), M1 D, 0< t1 ≤ T
С другой стороны
подставим V(M,t):
Противоречие. ч.т.д.
Следствие 1. Решение задачи(1), (2), (3) в цилиндре QT , непрерывное вплоть до границе, единственное.
Доказательство. Пусть u = u1 – u2 , u1, u2 - решения задачи.
По принципу максимума min u ≤ u ≤ max u, 0 ≤ u ≤ 0, значит u ≡ 0
ГT ГT
Следствие 2. Решение задачи (1), (2), (3) устойчиво по отношению к начальным и граничным условиям.
Т.е., если есть (1), (2), (3) и (1), (2*), (3*)
то, если
Доказательство: V = u – u*, V|t=0 = - *, V|MS = - *
|V|
≤ max(|
- *|,
- *|)
|V|
<
Существование решения краевой задачи для уравнения теплопроводности.
Рассмотрим первую краевую задачу для уравнения одной пространственной переменной.
Рассмотрим (1), (2), (3). Построим решение задачи методом Фурье
Задача (5), (6) на
собственные значения была рассмотрена
ранее. Известно, что она имеет нетривиальные
решения при
,
а соответствующие им собственные функции
имеют вид
Получили ряд Фурье,
где
, таким образом ряд Фурье (8), а следовательно
и (7), сходится равномерно и абсолютно
по х, так как (0)=0,
(l)
= 0, и
- кусочно-непрерывна.
При t
0, 0 < exp(-
t)
≤ 1
(7) сходится абсолютно
и равномерно по t,
следовательно u-
непрерывна в области. Покажем, что
.
То есть существует
ряд для
Рассмотрим (1), (2), (3)
u(x,0) = 0, f C, t > 0 (2)
f(0,t) = f(l, t) = 0
f – непрерывна и имеет кусочно-непрерывную производную по t.
Будем искать решение задачи в виде:
Тогда решение задачи (1), (2), (3):
(12)
В виду линейности рассмотренной задачи решение для (1), (2), (3) будет суммой (7) и (12). Рассмотрим (1), (2), (3). Возьмем w – непрерывную и дважды дифференцируемую функцию в области D : 0 ≤ x ≤ l, 0 ≤ t ≤ T, удовлетворяющую условиям (3):
Решение задачи
(1), (2), (3) будем искать в виде :
где V(x,t)
удовлетворяет уравнению:
V удовлетворяет начальным условиям : V(x,0) = 1(x)
V(0,t) = V(l, t) = 0
Решение задачи для V было нами получено.
Краевые задачи для уравнения теплопроводности общего вида.
Будем считать, что
При решении этой задачи мы находим счетное множество собственных чисел n и собственных функций n(M)
Подставим u
в начальное условие и получим :
Теорема. Решение задачи (1), (2), (3), непрерывное в заданной области вместе со своими частными производными первого порядка, единственно.
Доказательство: Допустим противное: существует 2 решения задачи (1), (2), (3): u1 и u2 . V = u1- u2 . V – удовлетворяет однородной задаче.
V|t
= 0
= 0
Первая формула
Грина:
Воспользуемся первой формулой Грина, положив u = V
Проинтегрируем это равенство по t от 0 до Т:
В левой части подынтегральная функция неотрицательная, значит интеграл в левой части 0, интегралы в правой части ≤ 0, значит выражения равны 0.
V
0
u1
u2
, значит
решение единственно.
Если α = 0, то используем принцип максимума.
Если β = 0, то тоже самое без второго слагаемого в краевом условии.
Задача Коши для уравнения теплопроводности.
Остановимся на изучении процесса распространения тепла в неограниченном стержне.
Из всех возможных условий на бесконечности, будем рассматривать условие ограниченности на бесконечности.
Теорема.
Решение задачи
,
,
непрерывное и
ограниченное, единственно.
Доказательство. Предположим, существует 2 решения: u1 и u2 .
Введем в рассмотрение
область В: {|x|
R,
0
t
T}.
Введем вспомогательную функцию:
На границе области В |V| |w|
То есть |V|
|w|,
то по принципу максимума:
Используя принцип максимума можно показать, что
Если рассматривать |V| |w(M,t)|. Фиксируем произвольную точку (x0,t0). Выбирая достаточно большое R, V(x0,t0) (*). Так как - произвольное, то соотношение (*) выполняется для всех точек области, значит V(x,t) 0.
Ч.т.д.
Вернемся к рассмотрению , . Будем искать
Так как - произвольная, то если воспользоваться всеми возможными , то
Это будет решением,
если интеграл равномерно сходится. При
некоторых условиях на
,
то есть при интегрируемости
Если функция периодическая, то этот ряд определяет функцию на всей числовой прямой.
Подставим наше решение в начальное условие:
Интеграл Фурье
для (х):
То есть мы получили явный вид решения задачи Коши.
(3) называется формулой Пуассона, интеграл справа называется интегралом Пуассона.
- фундаментальное
решение уравнения
теплопроводности.
Обоснование.
Пусть (х)
является
непрерывной и ограниченной.
.
Таким образом (3)
дает классическое решение
,
,
то есть u
– бесконечно дифференцируема и непрерывна
(
).
Покажем это:
Наряду с (3)
используется и другая формула. Вводится
замена
То есть получаемая по формуле Пуассона формула ограничена. Наличие экспоненциального множителя говорит о том, что этот интеграл сходится, и если будем дифференцировать, то получим сходящийся интеграл.
Покажем, что решение непрерывно примыкает к своему граничному условию:
Так как мы можем
выбрать достаточно большое L
:
Так как
- непрерывна, то
ч.т.д.
- функция Дирака.
- символ Кронекера;
;
Это соотношение выполняется для f, непрерывной на (-,+)
В каждом пространстве
Rn
, х = (х1,
. . ., хn)
можно определить
-функцию Дирака:
Пример. Рассмотрим точечную массу, помещенную в начале координат, распределенную на [-, ]
Проверим (**):
Если f(x)
– интегрируема на бесконечном интервале,
то для неё можно применить преобразование
Фурье:
По преобразованию Фурье однозначно находится функция :
Пример.
Так как - функция - четная, то её можно определить ещё и так:
Определение.
Функцией
Грина задачи Коши (1), (2) называется
функция
,
где M(x,y,z)
является решением задачи Коши.
-
- функция
Построим функцию
Грина для задачи
,
,
воспользовавшись
формулой Пуассона:
То есть фундаментальное решение задачи Коши является функцией Грина.
Физический смысл фундаментального решения.
Будем считать, что
в некоторый момент времени участку
сообщили количество
тепла
-
показывает на сколько повысилась
температура. В этом случае формула
Пуассона:
Уменьшаем начальный участок и стягиваем его к точке, то есть h 0. Но ранее воспользуемся теоремой о среднем:
То есть функция Грина определяет распределение температур в стержне в результате воздействия мгновенного точечного источника.
Решение этой задачи
:
- функция
удовлетворяющая уравнению:
Предложение.
Решение задачи Коши (1), (2) устойчиво по
отношению к начальным данным :
соответствующие
решения задачи:
Доказательство.
,
удовлетворяющая начальному условию:
Рассмотрим задачу
,
:
0
Решение этой задачи можно искать в виде суммы двух решений u = u1+ u2 , где
u1 соответствует задаче (1), (2), а u2 - ,
Для решения , рассмотрим вспомогательную задачу:
Будем считать, что f- непрерывная и ограниченная функция. Решение этой задачи по (3) имеет вид:
Решение задачи
,
можно получить в
виде:
,
покажем это:
Так как Р удовлетворяет
(*), то
удовлетворяет
,
.
Таким образом
решение задачи
,
имеет вид:
Задача для уравнения теплопроводности на полупрямой.
Лемма 1.
Если в (1), (2)
является нечетной относительно нуля
(
),
то
Доказательство. Решение задачи (1), (2) по формуле Пуассона :
Лемма 2.
Если в (1), (2) )
является четной относительно нуля (
),
то
Доказательство.
Пусть
Рассмотрим (1), (2),
(6). Продолжим
нечетным образом. U(x,
t)
удовлетворяет задаче с
Для (1), (2), (7) :
Запишем полученные решения через формулу Грина.
Для (1), (2), (6) :
Для (1), (2), (7) :
- функция Грина
или ядро Пуассона для (1), (2), (6)
-
функция Грина или ядро Пуассона для
(1), (2), (7)
Рассмотрим (1),
(2), (8).
- непрерывна на [0, ).
Продолжим начальные данные на отрицательную
полуось :
Будем считать в
дальнейшем, что Ф – непрерывная функция
:
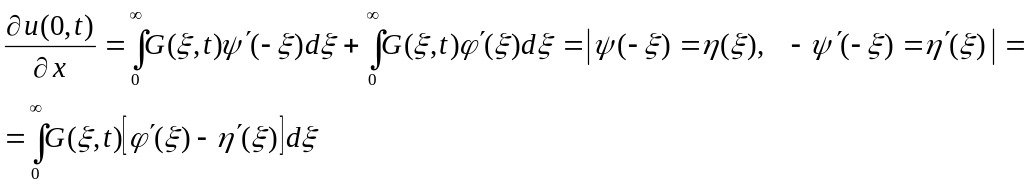
Поставим в (8):
Поменяем порядок интегрирования:
Построим решение начальной краевой задачи первого рода для неоднородного граничного условия.
Решение этой задачи в силу линейности можно записать u = u1 + u2 , где
u1 – решение (1), (2), (6), u2 - решения (1), (2), (6)
1.
-
решение задачи со
следующими условиями:
Тогда
- удовлетворяет задаче с условиями:
Формула U
определена для
Обычно U
доопределяется
следующим
образом:
,
2.Рассмотрим следующую вспомогательную задачу:
Пусть
Непосредственной проверкой можно убедиться, что
Пусть 
В этом
Тогда воспользовавшись теоремой о среднем
Тогда воспользовавшись
предельным переходом
Распространение тепла в пространстве.
(1)
а – коэффициент температуропроводности
(2)
Лемма. Пусть
в (1) и (2) функция
дополняет разделение переменных , то
решение этой задачи может быть в виде
Доказательство.
Удовлетворение функции и начальному условию очевидно.
G(M,P,t) – функция Грина для пространства M(x,y,z) , P(x,y,z)
Функция Грина представляет собой решение задачи
т.е. функция задающая начальное условие, может дополнить разделение переменных, то по лемме G- является произведением решений 3-х одномерных задач.
(3)
(4)
В случае неоднородности уравнения
(1’)
(2)
решение задачи
(1’),(2) ищется в виде
где
-
решение (1),(2)
-
решение (1’),(2’)
При этом сначала рассматривается задача
показать самостоятельно
Уравнения эллиптического типа.
U(M,t)=U(m)
уравнение Пуассона
уравнение
Лагранжа
Пусть имеется
единичная точечная масса М(x,y,z)
и в другой точке
,
масса m.
Ньютон вместо силы между 2-я массами предложил использовать потенциал
если имеется несколько точек, то
- уравнение Лапласа
Определение.
Функция U(M)
называется гармонической в D
(конечная область с кусочно- гладкой
границей D
),
если она непрерывна со своими частными
производными до 2-го порядка и удовлетворяет
уравнению Лапласа.
Определение. Функция U(M) называется гармонической в неограниченной области Е, если она непрерывна в Е вместе со своими частными производными до 2-го порядка , удовлетворяет уравнению Лапласа и убывает при стремлении
к
бесконечности, т.е.
Основные задачи для уравнения Лапласа и Пуассона.
1.Пусть D- ограниченная область с кусочно-гладкой границей, а Е- неограниченная область.
(2)- задача Дирихле может быть внутренней, если решается в D, внешней, если в E.
(3) – задача Неймана, n- внешняя нормаль к S.
(1) (4) – третья краевая задача.
Вид оператора Лапласа в криволинейных координатах
- сферические
координаты
- самостоятельно
- цилиндрические
координаты
Рассмотрим решение уравнения Лапласа в сферических координатах.
Будем считать, что решение обладает центральной симметрией
U(r,,)=U(r)
если положить
=1,
=0,
то получим U=1/r
– фундаментальное решение, это
гармоническая функция. Эта функция
непрерывна за исключением точки
.
Это фундаментальное
решение уравнения Лапласа в пространстве.
Для плоскости, полагая, что решение
обладает центральной симметрией
Если =-1, =0, то фундаментальное решение имеет вид U()=ln(1/).
Теорема1.Функция U(m), гармоничная в конечной области D, не может достигать даже локального максимума или минимума в точках D (D- не замкнутая), за исключением, когда Uconst.
Теорема2.U(m) гармонично в D и непрерывно вплоть до границы, достигает своего наибольшего (наименьшего) значения на границе области D.
Доказательство от противного.
Предположим, что
пусть существует внутренняя точка
)
в которой и достигает
своего максимального значения .
Опишем сферическую
поверхность радиуса
из точки
.Границу
этой сферической поверхности обозначим
Обозначим точки, лежащие внутри или на сфере через M(x,y,z) ,
Всегда можем
подобрать такое достаточно маленькое
,
что
Введем вспомогательную
функцию вида
Рассмотрим V(M) внутри сферы
отсюда следует
что V
принимает наибольшее значение внутри
сферы, пусть это точка
.
, M
сфере.
,
где
=0
Получим противоречие, т.е. V не может принимать максимальное значение во внутренней точке, отсюда следует что U не принимает максимальное значение во внутренней точке.
Следствие. Если V и U гармоничные в D и непрерывные вплоть до границы, то выполнение на границе одного из неравенств UV, UV влечет за собой выполнение этих неравенств во всей области . Это следует из U-V0
Пусть U и V являются непрерывными вместе со своими частными производными вплоть до второго порядка в D.
(5)
(5) – первая формула Грина.
Аналогично поменяв местами U и V, и вычитая это из (5) получим
(6)
(6)-вторая формула Грина.
(5) (6) – справедливы и тогда, когда D - многосвязная. В этом случае справа рассчитывается интеграл по всем ограничивающим поверхностям.
Замечание. Совершенно аналогично для плоского случая имеет место формула
(5’)
(6’)
Лемма. Пусть
U-
дважды непрерывно дифференцируема в D
с границей S
(достаточно гладкой) и имеет непрерывные
первые производные, непрерывные вплоть
до границы, тогда для произвольной
внутренней точки области
(7)
где r-вектор от до точки М.
Доказательство.
Будем сначала считать, что U имеет две производные, непрерывные вплоть до границы.
Введем в рассмотрение функцию V=1/r, применить к U и V функцию Грина непосредственно не можем, т.к. V в не определена.
Ограничим сферой
радиуса
точку
поверхность сферы.
В этой области применим вторую формулу Грина
Устремим к 0 слева
Оценим второй интеграл :
n=-r
При
0
т.к.
Очевидно получим формулу (7)
Чтобы избавиться от предположения двух производных вплоть до границы следует поступать так:
Рассмотрим
последовательность областей
будут непрерывны две производные и
справедлива (7) ,перейдем к пределу при
,
получим (7) для функций непрерывными
первыми производными вплоть до границы
.
Замечание.
Аналогичная формула справедлива и для
плоского случая
(7)
Пусть рассматриваемая функция является гармонической, то
(8)
Тогда, если
(8’)
Если U удовлетворяет уравнению Пуассона
Интеграл вида
называется
потенциалом объема
Интеграл вида
называется потенциалом простого слоя
Интеграл вида
называется потенциалом двойного слоя
Из второй формулы Грина для гармонической функции (6) вытекает следующее свойство гармонических функций.
Пусть U гармоническая в области D с границей S, то
Возьмем в (6) V1,
то
,
тогда задача Неймана для уравнения
Лапласа будет иметь решение, когда
(необходимое условие)
Сейчас и в дальнейшем будем полагать, что граница области D S является регулярная поверхность, т.е. в любой точке поверхности определенная нормаль.
Если в точке поверхности построить систему координат: z – направлена по нормали, x и y – располагаются в касательной плоскости, то уравнение поверхности можно записать в разрешенном виде
Теорема единственности.
Первая внутренняя краевая задача для уравнения Лапласа (Пуассона) имеет единственное решение.
Доказательство:
Предположим двух решений, удовлетворяющих (1) (2).
В силу непрерывности
решений
- функция, гармоничная в D
и удовлетворяет
По принципу
максимума
Теорема устойчивости.
Решение внутренней задачи Дирихле для уравнения Лапласа (Пуассона) устойчиво по отношению к граничным условиям.
Доказательство:
удовлетворяет
По принципу
максимума
Теорема. Решение внутренней задачи Неймана уравнения Лапласа (Пуассона) определяется с точностью до константы.
Доказательство:
Рассмотрим
внутреннюю задачу Неймана, будем считать
что
два решения
в силу линейности задачи и будет
гармонической в области и удовлетворять
Воспользуемся первой формулой Грина (5) положив V=U.
т.е. решение внутренней задачи Неймана не единственно.
Рассмотрим третью краевую задачу
Теорема. Решение третьей краевой задачи для уравнения Лапласа (Пуассона) единственно.
Доказательство:
Предположим
второго решения
гармонично в D.
Применим к U первую формулу Грина (6), положив U=V
Из граничного
условия
т.к.U0
Функция U(M),
определенная в некоторой области
-гладкая замкнутая поверхность, называется
регулярной на ,
если при М
U(M)<A/R,
R=OM
где О -начало координат, и
где А – const
Замечание. Можно показать, что функции, гармонические вне некоторой замкнутой поверхности S являются регулярными.
Теорема. Решение внешних краевых задач для уравнения Лапласа (Пуассона) единственно
Доказательство:
Выберем центр
координат внутри замкнутой поверхности
S
и проведем сферу
,
которая содержится внутри S.
-область
между S
и
.
Предположим, что
в
существует 2
решения, которые содержатся внутри S.
- область между S
и
.
Предположим, что в два решения то .Применим (5), полагая U=V в области
, где
Для задачи (1) (2) устремим R к
(*)
Т.е. пришли к (*) :gradU=0 U=const , U(M)=0 , ME (для (3))
Для (1) (2) gradU=0 U(M)=const , U0 , M U0