
- •Распространение тепла в пространстве.
- •Уравнения эллиптического типа.
- •Основные задачи для уравнения Лапласа и Пуассона.
- •Функция Грина задачи Дирихле.
- •Свойства функции Грина. Задачи Дирихле
- •Функция Грина задачи Неймана.
- •Построение функции Грина.
- •Следствие из формулы Пуассона.
- •Внешняя задача Дирихле для шара.
- •Решение задачи Неймана для шара.
- •Решение краевых задач для простейших областей методом Фурье.
- •Теорема о среднем значении (Гаусса).
- •Теория потенциалов. Несобственные интегралы зависящие от параметра.
- •Потенциал объема и его свойства.
Функция Грина задачи Дирихле.
Для функции U(M)
задача Дирихле U(M)=0
![]()
Введем
![]() :g
– гармоническая в D.
:g
– гармоническая в D.
![]()
Пусть
![]()
Применим к g и U вторую формулу Грина
![]() т.к. U
и g
гармонические
т.к. U
и g
гармонические
![]()
Вычтем
![]() из
:
из
:
![]()
В этой формуле присутствует только U на S.
Обозначим
![]()
![]() (*)
(*)
![]() -
функция Грина внутренней задачи Дирихле
для уравнения Лапласа.
-
функция Грина внутренней задачи Дирихле
для уравнения Лапласа.
Определение. Функцией Грина задачи Дирихле для уравнения Лапласа называется функция удовлетворяющая условиям:
1. гармоническая в D, исключая точку .
2.в
D
функция G
дополняет представление
![]() ,
,
где g - гармоническая в D
3.
На границе
![]() (следует из (*))
(следует из (*))
![]() - регулярная часть
функции Грина.
- регулярная часть
функции Грина.
Замечание.
Для плоскости G
имеет вид
![]() ,
тогда решение
внутренней задачи Дирихле для плоскости
,
тогда решение
внутренней задачи Дирихле для плоскости
![]()
L – достаточно гладкая граница конечной области B
Для пространства решение внутренней задачи Дирихле
![]() (9)
(9)
Свойства функции Грина. Задачи Дирихле
1.Функция Грина
![]()
В точке
![]() -
особенность, опишем вокруг
шар радиуса ,
это область
-
особенность, опишем вокруг
шар радиуса ,
это область
![]() .
В
G-
гармоническая и не константа
.
В
G-
гармоническая и не константа
![]() ,
при 0,
r0,
+.На
внутренней границе функция положительная,
значит
>0
по принципу максимума.
,
при 0,
r0,
+.На
внутренней границе функция положительная,
значит
>0
по принципу максимума.
2.
![]() -
симметричны.
-
симметричны.
Доказательство:
Рассмотрим две
произвольные точки в D:
![]() .
.
Рассмотрим
![]()
Рассмотрим область
-
полученную из D
вырезанием шаров радиуса
вокруг
![]() ,
границы этих шаров
,
границы этих шаров
![]()
В данной области применим вторую формулу Грина
![]() т.к. функции
гармонические
т.к. функции
гармонические
![]()
![]() внутри
внутри
![]()
![]()
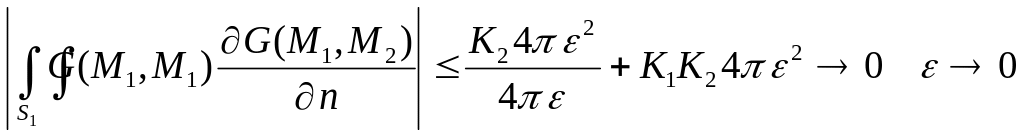

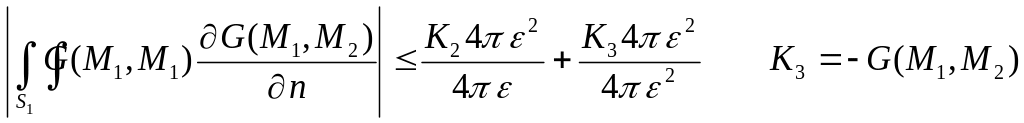

Здесь
![]()
![]()
Физический смысл,
если есть в М, источник, то он действует
на
![]() так же, как и действовал он на
,если
бы находился в
.
так же, как и действовал он на
,если
бы находился в
.
Рассмотрим установившееся распространение температур в результате действия постоянно действовавшего точечного источника.
![]()
![]()
Решение ищем в
виде
![]()
![]()
Из
опишем шар
![]() радиуса r,
целиком лежащий в D
и проинтегрируем это уравнение по
радиуса r,
целиком лежащий в D
и проинтегрируем это уравнение по
![]()
![]()
![]()
Используя формулу Остроградского-Гаусса
![]()
![]()
![]()
![]()
Функция Грина задачи Неймана.
U(M)=0
![]()
Введем :g – гармоническая в D.
![]()
Для U справедлива (8)
Введем в рассмотрение
![]()
Т.к. G и U гармонические, то применим вторую формулу Грина
![]() (*)
(*)
Вычтем (*) из (8) для функции U
![]()
Обозначим через![]() ,
тогда
,
тогда
![]()
Потребуем чтобы на S, G удовлетворяла условию
![]() ,где S
площадь поверхности S
,где S
площадь поверхности S
Тогда будет
выполнено
![]() .
Покажем это
.
Покажем это
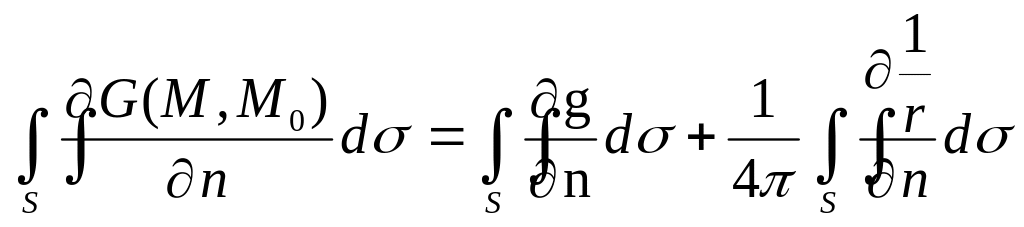 .
.
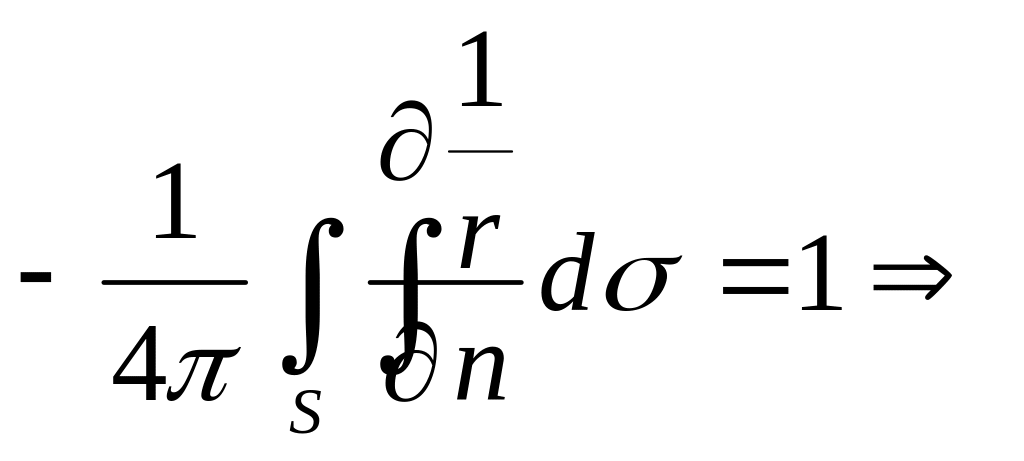
![]()
Ранее было
доказано, что для гармонической функции
![]() ,
чтобы задачи Неймана решение имеет вид
,
чтобы задачи Неймана решение имеет вид
![]() (10)
(10)
Вообще говоря функция Грина задачи Неймана не является симметричной.
Построение функции Грина.
Рассмотрим следующую задачу: построить функцию Грина задачи Дирихле для полупространства, ограниченного плоскостью z=0.
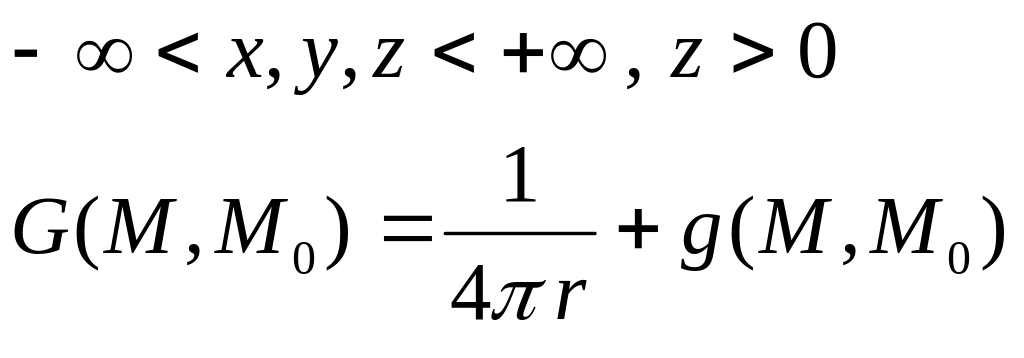

 z
M0(x0,y0,z0)
z
M0(x0,y0,z0)
0 y
x M1(x1,y1,z1)
Метод отражения:
из
на плоскость z=0
опускаем перпендикуляр и на продолжении
перпендикуляра выбираем
так, что для PS
![]() если
если
![]()
Эта функция гармоническая всюду в D и т.к. для PS
![]()
Замечание.
Для полуплоскости y>0
![]()
Построим решение внутренней задачи Дирихле для шара, найдя предварительно функцию Грина.
D :
:
![]()
P(
,
,
) Обозначим
![]() .
Выберем
вне шара
.
Выберем
вне шара
R следующим образом:
O r располагается на продолжении .
M0
M1
M1(x1,y1,z1)
![]()
![]() (*)
(*)
Выберем внутри шара произвольную точку P(,,)
![]()
![]()
Найдем
![]()
Рассмотрим
![]()
Они подобны, т.к.
у них есть общий угол и
![]()
![]() (**)
(**)
![]() всюду гармоничная
кроме точки P.
всюду гармоничная
кроме точки P.
Удовлетворяет свойствам функции Грина внутренней задачи Дирихле, тогда решение задачи записывается в виде
![]()
![]()

Аналогично
![]()
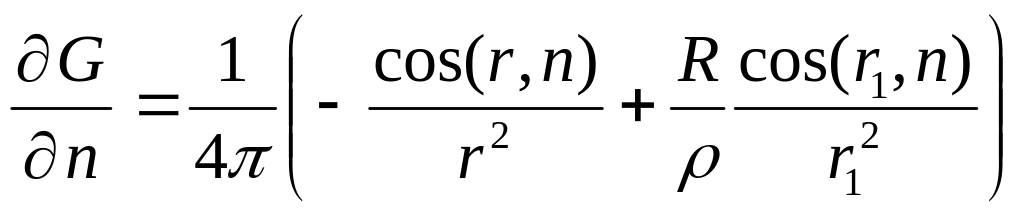
Из OP
по теореме косинусов
![]()
Из OP
![]()

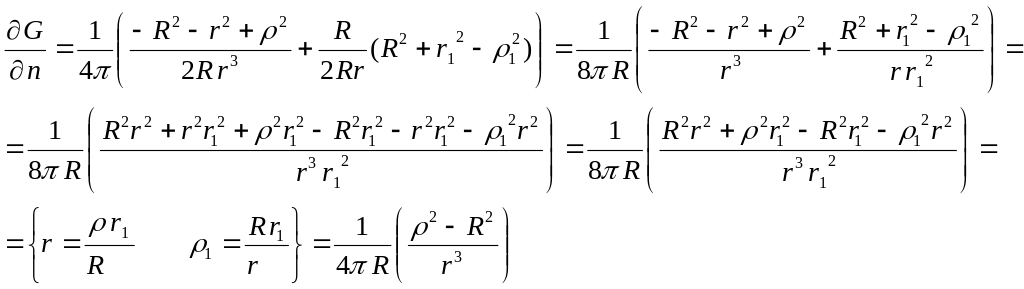
![]() (11) –это формула
Пуассона
(11) –это формула
Пуассона
Покажем гармоничность и считаем непрерывной
![]()
![]()
![]()
т.е. U(M)=0
Докажем, что если МN (NS), то U(M)(M).
Выберем произвольно NS, отметим что (11) справедлива, когда задача Дирихле очевидно имеет решение для (P)1, то U(M)=1,тогда
![]() (***)
(***)
![]()
Проведем из N сферу радиуса 2,

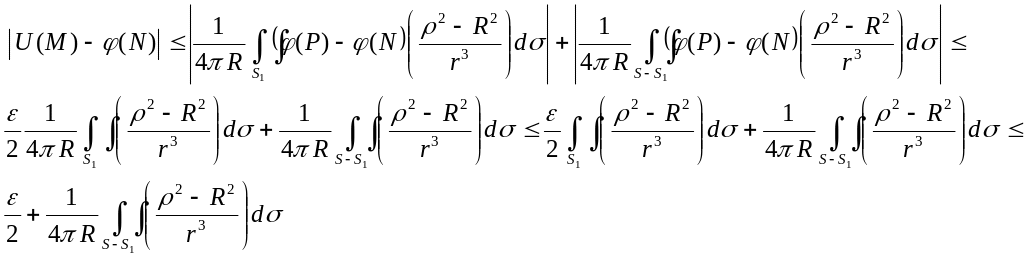
Проведем еще одну сферу радиуса
![]() для
для
![]()
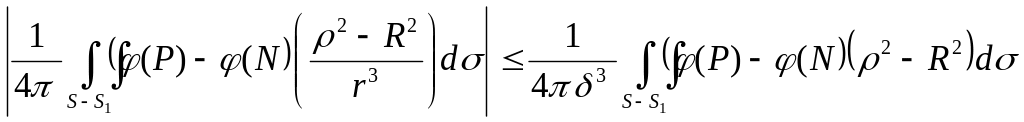 т.к. r>
т.к. r>
{т.к. U
непрерывна по замкнутой сфере, то она
ограниченна, то
![]() }
}
![]()
т.е.
![]()
т.е. (11) дает решение задачи Дирихле для шара.
Введем в рассматриваемой задаче сферические координаты
![]() -угол, то (11) примет
вид
-угол, то (11) примет
вид
 (12)
(12)
Для плоскости в полярных координатах (11) имеет вид
![]()
