Введение.

Знакомство с волновыми процессами (волнами) начнем с того, что вспомним о колебаниях, так как источником любой волны является колебание.

Колебательное движение (колебание) имеет огромное распространение в окружающем нас мире, поэтому его часто выделяют отдельно, хотя колебания механических систем полностью описываются механикой Ньютона. Колеблются грузы на пружинах, подвесах, колеблются струны роялей и скрипок, дома и мосты. Трясутся при проезде транспорта или сильном ветре, по дрожанию паутины пауки обнаруживают запутавшуюся в ней жертву, колеблются атомы в молекулах.

1. Колебания.

Колебанием называется движение или изменение состояния, обладающее той или иной степенью повторяемости. Физическая природа колебаний может быть различна (механические, электромагнитные), однако они могут быть описаны одинаковыми математическими закономерностями.

Колебания называются периодическими, если значения физических величин, изменяющихся в процессе колебаний, повторяются через равный промежуток времени, называемый периодом колебания.

Частным случаем периодических колебаний является гармоническое колебание, в котором изменяющаяся физическая величина X изменяется во времени по закону

(1.1) Х = А cos(ωt+φ) , где А – амплитуда, (ωt+φ) - фаза, φ - начальная фаза,

ω = 2π /Т = 2πν, где ω - рад/с, Т – период, т.е. время, за которое совершается 1 колебание.

Выражение (1.1) соответствует бесконечной косинусоиде, которая никогда не заканчивается. Некоторые процессы в реальном мире довольно хорошо могут быть описаны уравнением (1.1), например, колебание гармонического маятника, груза на пружине и т.д.

Модель гармонического колебания важна, прежде всего потому, что любой сложный периодический процесс может быть представлен суммой гармонических колебаний с кратными частотами (гармониками или обертонами), имеющих соответствующие амплитуды и фазы (разложение по теореме Фурье).

Разложение в ряд Фурье основано на предположении, что все имеющие практическое значение функции в интервале - π ≤ х ≤ π можно представить в виде сходящихся тригонометрических рядов (ряд считается сходящимся, если сходится последовательность частичных сумм, составленных из его членов)

(1.2) F(x) = А₀ + A₁ cosωt + A₂ cos2ωt + А₃ cos3ωt + …..+ B₁sinωt + B₂ sin2ωt +…

Коэффициенты: А₀, А₁, Аn ,В₁ ,Вn - коэффициенты Фурье, А_{0 =} , Аn = 1/2π Вn = 1/2π dx . Если коэффициенты An, Bn можно вычислить, то ряд называется рядом Фурье, соответствующим F(x). Для точного представления сложного сигнала требуется бесконечное число членов ряда, однако для многих практических задач достаточно рассмотреть только несколько первых членов ряда.

Примеры;

1/ Пусть функция задана F(x) = { 0 при - π ≤ х ≤ 0,

{ 1 при 0 х ≤ π , тогда

А₀ = 1/π = 1 , An = 0 , Bn =1/π = ,

F(x) = 1 +

Такая функция может хорошо описать, например, звуковой щелчок.

2/ Пусть функция задана F(x) = { 0 при - π ≤ х 0,

Sin х при 0 х ≤ π , тогда

А₀ = 2/π , Bn = 0, B₁ = ½ ,

F(x) = 1/π + ½ sin x – 2/π

2/ пусть функция задана F(x) = 2х, разложение в ряд имеет вид

2х = 4 [(Sinх – ½ Sin2х +1/3 Sin3х – ¼ Sin4х + 1/5 Sin5x )]

4/ Пример спектрального разложения куска гармоники.

1.2.1. Условие существования в системе гармонических колебаний .

Если в системе происходит гармоническое колебание некоторой величины Х = Аcos (ωt+φ) , то скорость Х и ускорение Х этого процесса будут

= - А ω sin (ωt+), = - Аω² cos (ωt+φ) = - ω² Х

На рисунке отклонение частицы от положения равновесия обозначено буквой S. Тогда гармоническое колебание S= Acos (ωt+φ) описывает смещение конкретной частицы в зависимости от времени S(t).

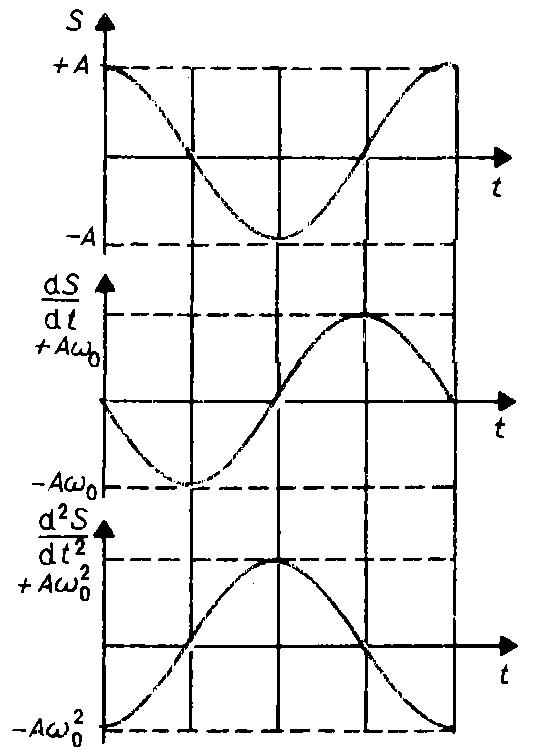
Умножив обе стороны уравнения на m , получим

F= - mω² Х = - kХ или + ω² Х = 0 (**)- уравнение гармонического осциллятора. Уравнения вида x=Acos(ωt+φ) или x=Asin(ωt+φ) являются решениями этого уравнения. Для того чтобы в системе возникли колебания, необходимо вывести систему из состояния равновесия. Если в системе возникает сила, пропорциональная этому смещению и направленная к состоянию равновесия F = - k X , то в такой системе будут происходить гармонические колебания с собственной частотой ω₀ и Т = 2π/ .

Примеры гармонических колебаний:

а/ пружинный маятник – это материальная точка массы m, закрепленная на абсолютно упругой пружинке и совершающая колебания под действием силы F = - k_упрX,

k_упр = mω². T = 2π /ω.

б/ ареометр - устройство для определения плотности жидкости.

Для определения плотности жидкости в нее помещают запаянную ампулу. Ампула устанавливается вертикально и находится в состоянии равновесия, так как сила Архимеда уравновешивает силу земного притяжения ( mg = F _арх = l₀Sρ_ж g, где l₀S – объем погруженной части ампулы, ρ_ж плотность жидкости, в которую погружен ареометр). Если ампулу немного сместить вниз на х, то нарушается равенство сил и возникает результирующая сила , направленная к состоянию равновесия

F = F арх - mg = (l₀ + x ) Sρ_жg – l₀ Sρ_жg = Sρ_жgx , mω² = Sgρ_ж

ω_{0 = , T} = 2π , где ρ = ρ_ж .

в) колебания физического маятника

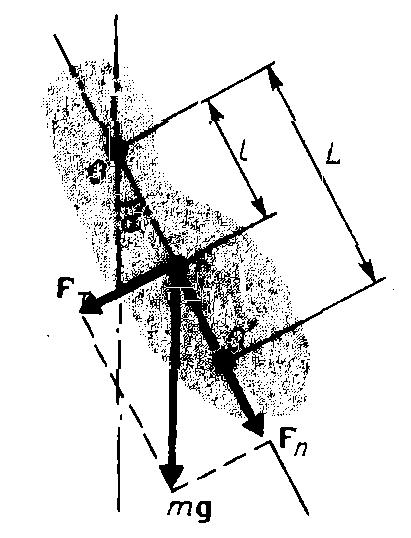
Если любое тело (физический маятник) отвести от положения равновесия, то возникает момент силы тяжести, возвращающий тело к состоянию равновесия согласно основному закону вращательного движения

М = Iβ = I = - mgh sinθ ,

+ sinθ = 0 , здесь I –момент инерции тела относительно точки подвеса, h-расстояние от точки подвеса до центра масс (на рис. Обозначено как l).

При малых θ sinθ~ θ . На рис. θ =ά. Сравнив эту формулу с общим уравнением, получим, что

ω = , Т = 2π

Измерения периода колебаний тела относительно некоторой оси могут быть использованы для определения момента инерции тела относительно этой оси.

Физическим маятником может быть любое тело, участвующее в периодическом движении, например, нога при ходьбе при каждом шаге совершает полупериод колебаний.

Колебания маятника используются в геологии для анализа неоднородностей земной коры.

г) свободные колебания в идеализированном колебательном контуре.

Колебательный контур – цепь, состоящая из последовательно включенных конденсатора С, индуктивности L и резистора R. Если R = 0, то в системе возникают колебания электрического и магнитного полей. При t = 0 ключ в контуре замыкают, и предварительно заряженный конденсатор начинает разряжаться через катушку индуктивности контура.

В каждый момент времени напряжение на обкладках конденсатора равно разности потенциалов на катушке

U = = - L ,

Когда конденсатор полностью разряжается Q = 0 , то сила тока в контуре достигает максимального значения

- L = , I =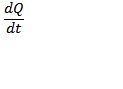 , = 0

Сравнив это уравнение с уравнением (**), определяем решение Q = Q₀ cos (ωt ₊ φ) ,

I = - Q₀ωsin ( ωt + φ), где

ω = 2πf = ,

Из последних выражений следует, что колебания тока опережают по фазе колебания заряда Q на π/2 , т.е. ток достигает максимальное значения, когда заряд обращается в нуль и наоборот.

Энергия, запасенная в электрическом поле конденсатора W_E =Q²/C =Q₀²cos ² (ωt + φ). Энергия, магнитного поля катушки W_H =Q₀²sin² (ωt + φ ) , Тогда полная энергия колебаний W _{полная =} = Q₀² остается постоянной во времени.

1.2.2 Энергия в гармонических колебаниях.

Система, совершающая гармоническое колебание, называется гармоническим осциллятором.

Энергия системы, участвующей в гармоническом процессе, состоит из энергии движения

Е_кин и энергии положения Е_пот ( потенциальной)

Е_полная = Е_кин + Е_пот , Е_кин = mv² /2 = A²ω² cos² (ωt+φ) ,

= - , Е_пот = - = kx²/2 , где k – коэффициент в выражении силы

Е_пот = mω²A² sin² ( t+)/2, E= = Е_кин + Е_пот = mω²A² /2

Если в системе происходит гармоническое колебание, то полная механическая энергия системы должна оставаться неизменной.

1.2.3. Затухающие колебания.

За счет действия сил трения и других сил сопротивления механическая энергия системы уменьшается, так как при этом энергия системы постепенно переходит в тепло и амплитуда колебаний уменьшается. Сила сопротивления F часто пропорциональна скорости F = - bv = - b . Тогда F = - mω² x – b = md²x/dt²

+ + ω² x = 0

Если уменьшение энергии происходит медленно, т.е. b – мало, то решение уравнения имеет вид

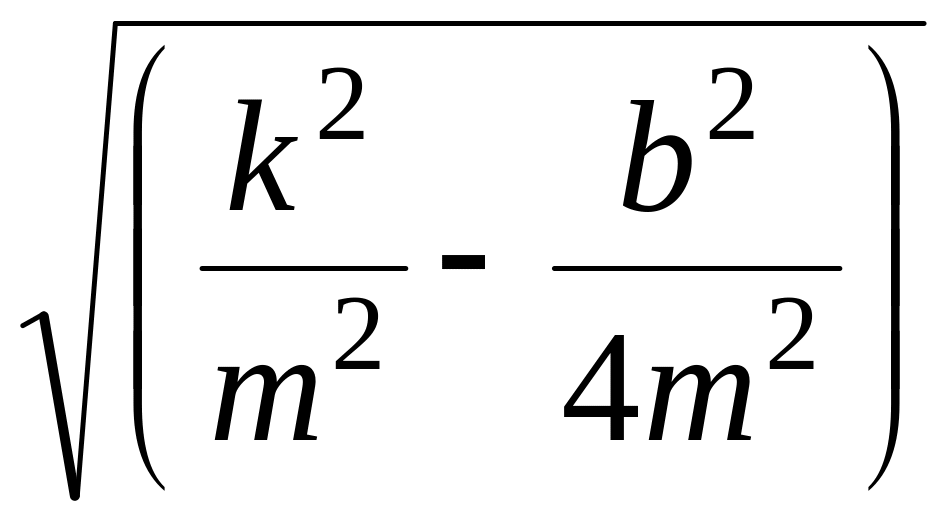
X = А exp (-βt ) sinω’t, где β = , , т.е. колебание можно рассматривать как гармонические , на которые накладывается затухание.

На практике, когда затухание невелико (трение мало) b = mω₀, то ω’ мало отличается от ω₀.

Промежуток времени t₁ = 2m/b, за который амплитуда колебаний уменьшается в е раз, называется временем релаксации. Чем больше b, тем быстрее колебание прекращается. Если b = ½ mω₀, то затухание значительное, если b = mω₀, то затухание закритическое и настолько велико, что если b ≥ 4mk, то ω становится мнимой величиной. В этом случае система просто возвращается в положение равновесия, не совершая колебаний.

Демпфирование колебаний ( искусственное создание режима докритического или критического затухания) используется в устройствах закрытия дверей, амортизаторах автомашин, для успокоения стрелок измерительных приборов ( вольтметров, амперметров, индикатор уровня ).