13. Алгебры с одной б.А.О. Полугруппа. Моноид. Группа.

Алгеброй называется упорядоченная пара (А, Ω), состоящая из А≠Ø (основное множество алгебры) и Ω (совокупность операций на множестве А – главные операции алгебры).

А=<А, Ω >

Тип алгебры А=<А,f₁,…,f_k> - это последовательность, состоящая из рангов n-арных операций, т.е. (rang (f₁),…,rang (f_k))

Алгебра g=<G,*> типа (2) называется полугруппой, если *-ассоциативна => G - полугруппа.

Алгеброй g=<G,*,1> типа (2,0) называется моноидом, если:

1) * - б.а.о. – ассоциативна на G

2) нейтральный элемент в g относительно б.о. *, т.е. моноид – это полугруппа с нейтральным элементом. Моноид – полугруппа с 1.

Алгебра g=<G,*,’> типа (2,1) называется группой, если:

1. * - ассоциативна, т.е. (a*(b*c))=(a*b)*c

2. e ϵ g:a*e=e*a=a, ∀ a ϵ g

3. ∀ x ϵ g x’ ϵ g:x*x’=e

Группа – это моноид, в котором каждый элемент симметризуем.

Группа с коммутативной операцией называется коммутативной или абилевой

Если множество А конечно то можно составить таблицу кеш

Таблица кеш – таблица, которая описывает структура алгебраических систем с одной бинарной операцией

14. Алгебры с двумя а.О. Кольца. Поля.

Алгебра =(K,+,*) – типа (2,2) – наз. Кольцом (не ассоциативным), если для операций наз. Сложением и умножением выполн. След. Св-ва.

1. Коммутативность

2. Ассоциативность

3. 

4. 

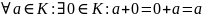
5. Дистрибутивность

Если умножение в кольце коммутативно, то кольцо наз. Коммутативным кольцом

Если умножение в кольце ассоциативно, то оно наз. Ассоциативным кольцом

Если. < , ∙> - полугруппа, тогда эта структура наз. Мультипликативной полугруппой кольца

Если относительно умножения в кольце есть нейтральный эл-т 1, то кольцо наз. Кольцом с единицей

Не нулевой эл-т кольца А наз. Левым (правым) делителем 0, если т.е (b ) : для => a – левый делитель нуля

Если умножение в кольце коммутативно, то левые и правые делители совпадают.

Алгебра <F,+, ∙> наз. Полем, если для б.о. +,* выполняются след. Св-ва

1. a+b=b+a

2. a+(b+c)=(a+b)+c

3. ∃0∈F : a+0=a

4. ∀ a∈F ∃ ! a’∈F : a+a’=0

5. (a*b)*c=a*(b*c)

6. a*b=b*a

7. ∃ 1∈F : a*1=a

8. ∀ a≠0 ∃ a’∈F : a*a’=1

9. 1≠0

10. a(b+c)=ab+ac

<F,+> - абелева адитивная группа поля

<F\{ },∙> - мультипликативная группа поля

Поле – это ассоциативное, коммутативное кольцо с 1, в которой 0 1 и каждый не нулевой эл-т обратим.

Элемент а называется обратимым (делитель 1) в кольце К, если для него существует обратный элемент в этом кольце

Существует a’ из К a∙a’=a’∙a=a

15. Гомоморфизм алгебр.

Пусть А=<A, Ω >, B=<B, Ω ‘> - однотипные алгебры, т.е. главных операций Ω на А столько, сколько главных операций Ω’ на В.

Пусть f_a – главная операция на А, f_b – главная операция на В.

Отображение h: A →B сохраняет главную операцию f_a, если ∀ а₁…а_n ϵ A h((f_a)(a₁…a_n))=f_b(h(a₁)…h(a_n)), где n – ранг операции f_a.

Гомоморфизмом алгебры А→В называется отображение h:A→B, которое сохраняет все главные операции A.

Гомоморфизм h:A→B называется мономорфизмом, если h – инъективное отображение A→B.

Гомоморфизм h:A→B называется эпиморфизмом, если h – сюръективное отображение A→B.

Гомоморфизм h:A→B называется изоморфизмом, если h – биективное отображение A→B.

Гомоморфизм алгебры A→B называется эндоморфизмом.

Изоморфизм алгебры А на себя называется автоморфизмом.