32. Комплексные корни

33. Многошаговый метод Адамса

Многошаговые методы появились гораздо раньше, чем методы Рунге − Кутты. Впервые их получил Дж.К. Адамс еще в 1855 г. Тем же способом, что и Адамс, выведем первое семейство многошаговых методов (Адамса − Башфорта).

Предположим, для задачи Коши (1.8):

нам известны первые r + 1 решения   на равномерной сетке   с шагом h. Тогда для шага r + 1 формально решение можно представить как

(5.1)

Заменим подынтегральную функцию на ее интерполирующий полином Ньютона, полученнsq по узловым значениям  :

(5.2)

где разделенные разности вычисляются из треугольника

Тогда численный аналог (5.1) будет задаваться формулой

(5.3)

Согласно (5.3) для r = 0, 1, 2 получаем следующие явные формулы Адамса:

Формулы Адамса получаются при интегрировании интерполяционного многочлена (5.2) от   т.е. вне интервала интерполяции. Однако, как мы знаем, вне этого интервала интерполяционный многочлен обычно дает довольно плохое приближение. Таким образом, явные методы Адамса не очень точны. Чтобы разрешить эту проблему, Адамс предложил для интерполяции использовать значение   вместо   В итоге он получил неявные методы (Адамса − Мультона). Приведем первые из них для r = 0,1:

Итак, любой s-шаговый метод Адамса можно представить в общем виде

(5.4)

где   — постоянные метода. Если  , метод явный, иначе — неявный. Порядок метода определяется точностью интерполирующей формулы (5.2). В общем случае явный метод (5.4) имеет порядок p = s, неявный — p = s + 1.

БИЛЕТ 18_______________________________

34. Метод простой итерации для решения системы

Метод простых итераций для решения (1) аналогичен методу, рассмотренному при решении нелинейных уравнений с одним неизвестным. Прежде всего, выбирается начальное приближение  , а исходная система уравнений преобразуется к эквивалентной системе вида

, (5)

и по ней осуществляется итерационный цикл. Если итерации сходятся, то они сходятся к решению уравнения (1). Обозначим  . Достаточным условием сходимости является  . Скорость сходимости метода сильно зависит от вида конкретно подбираемых функций  , которые должны одновременно удовлетворять условиям эквивалентности (5) и (1), и обеспечивать сходимость итерационного процесса.

Например, для исходной системы уравнений   эквивалентная итерационная система (5) может быть представлена в следующем виде:

,

где множители   = –0.15 и   = –0.1 подбираются из анализа условий сходимости.

35. Задача Дирихле для уравнения Лапласа

Распределение тепла в теле называется стационарным, если температура   тела зависит от положения точки  , но не зависит от времени  , т. е.

.

В этом случае

и функция   удовлетворяет уравнению

.

Определение. Функция   называется гармонической на области  , если она имеет непрерывные частные производные второго порядка на   и удовлетворяет на   уравнению

.                                                 (1)

Уравнение (1) называется уравнением Лапласа. Справедлива

Теорема 1. Пусть ограниченная область   пространства имеет кусочно-гладкую границу (поверхность)  , на которой задана непрерывная функция  . Тогда существует на замыкании   единственная непрерывная функция  , гармоническая на  , такая, что

.

Теорема 1 имеет очевидную физическую интерпретацию. Если на границе   тела   все время поддерживать температуру  , равную  , где   - заданная непрерывная на   функция, то внутри тела установится вполне определенная (единственная) температура  . Это утверждение с физической точки зрения надо считать очевидным. Но оно может быть доказано и математически. Эта задача, называемая задачей Дирихле, исследована очень хорошо, при этом даются различные приближенные методы ее решения.

Задача Дирихле имеет большое практическое применение и в плоском случае. В плоском случае она формулируется так.

На кусочно-гладкой границе   плоской области   задана непрерывная функция  . Требуется найти функцию , непрерывную на   и гармоническую на  , т. е. имеющую вторые непрерывные частные производные и удовлетворяющую уравнению Лапласа на  :

.

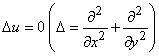Эта задача решается положительно: на   существует и притом единственная функция  , удовлетворяющая  требованиям этой задачи.

Особенно важны те случаи, когда задача Дирихле решается эффективно

БИЛЕТ 19_________________________________