
- •9.Повторение испытаний, формула Бернулли.
- •10. Случайные величины, дискретные и непрерывные случайные величины.
- •11.Закон распределения дискретной случайной величины. Примеры.
- •16.Дисперсия появления события а в одном и нескольких независимых испытаниях.
- •17.Мат.Ожидание, дисперсия и среднее квадратичное отклонение среднего арифметического одинаково распределенных взаимно независимых случайных величин.
- •23. Нормальная кривая, ее вид при различных значениях параметров.
- •29. Критические точки и критические области распределения
- •30. Генеральная и выборочная совокупности.
- •32Точечные оценки параметров распределения.
- •36.Статистическое распределение двумерной величины (корреляционная таблица). Среднее значение и среднее квадратичное отклонение составляющих.
23. Нормальная кривая, ее вид при различных значениях параметров.
График
плотности нормального распределения
называют нормальной кривой (кривой
Гаусса).Исследуем функцию у=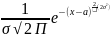 1.Очевидно,функция
определена на всей оси х;2 При всех
значениях х функция принимает положительные
значения ;3. Предел функции при
неограниченном возростании х равен
нулю ;4.Исследуем функцию на экстремиум.Найдем
производную : у
1.Очевидно,функция
определена на всей оси х;2 При всех
значениях х функция принимает положительные
значения ;3. Предел функции при
неограниченном возростании х равен
нулю ;4.Исследуем функцию на экстремиум.Найдем
производную : у =-
=-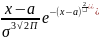 Видно,что
уˈ=0 при х=а,уˈ>0 при х<а,уˈ<0 при
х>а.Следовательно ,при х=а функция
имеет максимум равный 1\(
Видно,что
уˈ=0 при х=а,уˈ>0 при х<а,уˈ<0 при
х>а.Следовательно ,при х=а функция
имеет максимум равный 1\(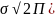 5.
Разность х-а содержится в анлитическом
выражении функции в квадрате .6. При
х=а+
и х=
5.
Разность х-а содержится в анлитическом
выражении функции в квадрате .6. При
х=а+
и х= вторая производная равна нулю,а при
переходе через эти точки она меняет
знак. Известно,что графики функций f(x)
f
(x-
вторая производная равна нулю,а при
переходе через эти точки она меняет
знак. Известно,что графики функций f(x)
f
(x- имеют
одинаковую форму; сдвинув график f(x)
в положительном направлении оси х на а
единиц масштаба при а >0 или в
отраправленицательном направлении
при а<0,получим график f(x-a)Отсюда
следует,что изменение величины параметра
а не изменяет формы нормальной кривой,п
приводит лишь к ее сдвигу вдоль оси Ох
:вправо,если а возрастает, и влево,если
а убывает. По-иному обстоит дело,если
изменяется параметр
. С возростанием
максимальная
ордината нормальной кривой убываент
,а сама кривая становится более пологой,она
сжимается к ос Ох ; при убывании
нормальная кривая становится более
«островершинной» и растягивается в
положительном направлении оси Оу.
имеют
одинаковую форму; сдвинув график f(x)
в положительном направлении оси х на а
единиц масштаба при а >0 или в
отраправленицательном направлении
при а<0,получим график f(x-a)Отсюда
следует,что изменение величины параметра
а не изменяет формы нормальной кривой,п
приводит лишь к ее сдвигу вдоль оси Ох
:вправо,если а возрастает, и влево,если
а убывает. По-иному обстоит дело,если
изменяется параметр
. С возростанием
максимальная
ордината нормальной кривой убываент
,а сама кривая становится более пологой,она
сжимается к ос Ох ; при убывании
нормальная кривая становится более
«островершинной» и растягивается в
положительном направлении оси Оу.
24.
Если предполагается нормальное
распределение признака в генеральной
совокупности, то получить ответ на этот
вопрос очень просто. Как говорилось
ранее, вероятность попадания нормально
распределенной случайной величины в
заданный интервал
![]() можно
определить по функции распределения:
можно
определить по функции распределения:
![]() или
с помощью функции плотности вероятностей:
P(x1<X<x2)=
или
с помощью функции плотности вероятностей:
P(x1<X<x2)=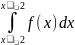 Итак, вероятность попадания с.в. U-->N(0;1)
в заданный интервал:
Итак, вероятность попадания с.в. U-->N(0;1)
в заданный интервал:
![]() ,где
Ф — принятое обозначение для функции
нормированного нормального распределения
которое имеет следующий вид:
,где
Ф — принятое обозначение для функции
нормированного нормального распределения
которое имеет следующий вид:
![]() , при
этом
, при
этом
![]() .Часто
представляет интерес вероятность
попадания с.в. U-->N(0;1) в симметричный
интервал. Тогда
.Часто
представляет интерес вероятность
попадания с.в. U-->N(0;1) в симметричный
интервал. Тогда![]() Учитывая
свойства функции Лапласа, получаем.
Интеграл, входящий в выражение, не
выражается в элементарных функциях,
поэтому для вычисления функции Ф(u)
используют вспомогательную функцию —
функцию Лапласа (интеграл вероятностей):
Учитывая
свойства функции Лапласа, получаем.
Интеграл, входящий в выражение, не
выражается в элементарных функциях,
поэтому для вычисления функции Ф(u)
используют вспомогательную функцию —
функцию Лапласа (интеграл вероятностей):
![]() который
табулируется. Функция Лапласа является
нечетной, т.е. Ф0(-u)=–Ф0(u).В
книгах по теории вероятности приведена
либо таблица значений функции Лапласа
который
табулируется. Функция Лапласа является
нечетной, т.е. Ф0(-u)=–Ф0(u).В
книгах по теории вероятности приведена
либо таблица значений функции Лапласа
![]() ,
либо
,
либо
![]() .Чтобы
найти вероятность попадания нормально
распределенной случайной величины
.Чтобы
найти вероятность попадания нормально
распределенной случайной величины
![]() в
заданный интервал
в
заданный интервал
![]() с
помощью функции Лапласа, сначала с.в. Х
нормализуется, а затем используется
следующая формула:
с
помощью функции Лапласа, сначала с.в. Х
нормализуется, а затем используется
следующая формула:
![]()
![]() Преобразуя формулу Лапласа-нечётную
(P(
Преобразуя формулу Лапласа-нечётную
(P(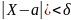 )=2Ф(
)=2Ф(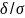 )),
положив
)),
положив
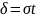 .
Получим P(|X-a|<
t)=2Ф(t)
Правило
3-х сигм : если случайная величина
распределена нормально,то абсолютная
величина ее отклонения от мат ожидания
не превосходит утроенного среднего
квадратичного отклонения. На практике
правило трех сигм применяется так: если
распределние изучаемой величины
неизвестно,но условие,указанное в
приведенном правиле,выполняется,то
есть основание предпологать,что изучаемая
величина распределена нормально ; в
противном случае она не распределена
нормально.
.
Получим P(|X-a|<
t)=2Ф(t)
Правило
3-х сигм : если случайная величина
распределена нормально,то абсолютная
величина ее отклонения от мат ожидания
не превосходит утроенного среднего
квадратичного отклонения. На практике
правило трех сигм применяется так: если
распределние изучаемой величины
неизвестно,но условие,указанное в
приведенном правиле,выполняется,то
есть основание предпологать,что изучаемая
величина распределена нормально ; в
противном случае она не распределена
нормально.
25.
Понятие о центральной предельной
теоремеЦентральная
предельная теорема была открыта русским
математиком А. М. Ляпуновым. «Если
случайная величина Х представляем собой
сумму очень большого числа взаимно
независимых случайных величин, влияние
каждой их которых на всю сумму ничтожно
мало, то Х имеет распределение, близкое
к нормальному» Пускай Х1,
Х2,…,Хn…-последовательность
независимых случайных величин, каждая
из которых имеет конечные математическое
ожидание и дисперсию: M(Xk)
=ak.
D(Xk)=bk2.
Введем обозначения:
![]() Обозначим
функцию распределения нормированной
суммы через
Обозначим
функцию распределения нормированной
суммы через
![]() .
Говорят, что к последовательности Х1,
Х2,…
применима центральная предельная
теорема, если при любом
х
функция распределения нормированной
суммы при n
.
Говорят, что к последовательности Х1,
Х2,…
применима центральная предельная
теорема, если при любом
х
функция распределения нормированной
суммы при n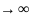 стремится к нормальной функции
распределения:
стремится к нормальной функции
распределения:
![]() В частности, если все случайные велечины
Х1,
Х2,…одинаково
распределены, то к этой последовательности
применима центральная предельная
теорема, если дисперсии всех величин
Хі(і=1,2,…)конечны
и отличны от нуля. А. М. Ляпунов доказал,
что если для
В частности, если все случайные велечины
Х1,
Х2,…одинаково
распределены, то к этой последовательности
применима центральная предельная
теорема, если дисперсии всех величин
Хі(і=1,2,…)конечны
и отличны от нуля. А. М. Ляпунов доказал,
что если для
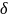 >0
при n
отношение Ляпунова
>0
при n
отношение Ляпунова
![]() стремится
к нулю, то к последовательности Х1,
Х2,…применима
центральная предельная теорема. Сущность
условия Ляпунова состоит в требовании,
чтобы каждое слагаемое суммы
стремится
к нулю, то к последовательности Х1,
Х2,…применима
центральная предельная теорема. Сущность
условия Ляпунова состоит в требовании,
чтобы каждое слагаемое суммы
![]() оказывало
на сумму ничтожное влияние.
оказывало
на сумму ничтожное влияние.
26.
Асимптотические формулы Лапласа
Локальная
теорема Муавра-Лапласа. Если npq
> 9,
то для расчетов используют приближение
Муавра-Лапласа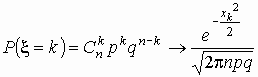 ,
где 0 < p
<
1 , величина
,
где 0 < p
<
1 , величина
![]() ограничена
при n
ограничена
при n
![]() .
Требование ограниченности величины xk
означает, что при n
величина
k
тоже должна расти вместе с величиной
n.
Точность формулы
.
Требование ограниченности величины xk
означает, что при n
величина
k
тоже должна расти вместе с величиной
n.
Точность формулы
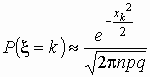 растет,
как с ростом величин n
и k,
так и по мере приближения к 0.5 величин
p и
q.Исследуем
точность асимптотической формулы
Муавра-Лапласа на следующем примере.ПРИМЕР
2.
Точность
формулы Муавра-Лапласа.Вычислим
вероятность того, что случайная величина,
имеющая биномиальное распределение,
принимает значение, равное n/2
. Выполним вычисления для n
= 10, 20, 50.
Сравним результаты вычислений по формуле
Бернулли и по приближенной формуле
Муавра-Лапласа. Интегральная теорема
Муавра-Лапласа. При n
для
схемы Бернулли при любых a
и b
справедлива
формула
растет,
как с ростом величин n
и k,
так и по мере приближения к 0.5 величин
p и
q.Исследуем
точность асимптотической формулы
Муавра-Лапласа на следующем примере.ПРИМЕР
2.
Точность
формулы Муавра-Лапласа.Вычислим
вероятность того, что случайная величина,
имеющая биномиальное распределение,
принимает значение, равное n/2
. Выполним вычисления для n
= 10, 20, 50.
Сравним результаты вычислений по формуле
Бернулли и по приближенной формуле
Муавра-Лапласа. Интегральная теорема
Муавра-Лапласа. При n
для
схемы Бернулли при любых a
и b
справедлива
формула
![]() Отсюда
следует, что вероятность того, что число
успехов в n
испытаниях Бернулли заключено между
k1
и k2,
можно вычислить по формуле
Отсюда
следует, что вероятность того, что число
успехов в n
испытаниях Бернулли заключено между
k1
и k2,
можно вычислить по формуле
![]() ,где
,где
![]() ,
,
![]() ,
,![]() -
функция Лапласа.Точность
этой приближенной формулы растет с
ростом n.
Если значение npq
сравнительно
невелико, то лучшее приближение дает
формула
-
функция Лапласа.Точность
этой приближенной формулы растет с
ростом n.
Если значение npq
сравнительно
невелико, то лучшее приближение дает
формула
![]() ,и
для вычисления вероятности того, что
число успехов в n
испытаниях
Бернулли заключено между k1
и k2,
можно использовать формулу
,и
для вычисления вероятности того, что
число успехов в n
испытаниях
Бернулли заключено между k1
и k2,
можно использовать формулу
![]() ,
где
,
где
![]() ,
,
![]() ПРИМЕР
3.
Точность
интегральных формул Муавра-Лапласа.Вероятность
рождения мальчика p
= 0.51, а девочки
- q = 1
- p = 0.49. Найдем
вероятность того, что среди 10
000новорожденных мальчиков будет не
менее 4 000 и не более 5000. Вычисления
проведем по формуле Бернулли и по
приближенным интегральным формулам
Муавра-Лапласа.
ПРИМЕР
3.
Точность
интегральных формул Муавра-Лапласа.Вероятность
рождения мальчика p
= 0.51, а девочки
- q = 1
- p = 0.49. Найдем
вероятность того, что среди 10
000новорожденных мальчиков будет не
менее 4 000 и не более 5000. Вычисления
проведем по формуле Бернулли и по
приближенным интегральным формулам
Муавра-Лапласа.
27.
Теорема Пуассона.
При большом количестве испытаний
вычисления по формуле Бернулли становятся
затруднительными. Однако в ряде случаев
их можно заменить более простыми
асимптотическими
формулами.
Одна из них основана на теореме Пуассона.
Если число испытаний n
и
p 0
так, что np
, > 0,
то![]() при
любых k =
0, 1, 2, … . Это означает, что при больших
n
и малых p
вместо вычислений по точной формуле
при
любых k =
0, 1, 2, … . Это означает, что при больших
n
и малых p
вместо вычислений по точной формуле
![]()
![]() можно
воспользоваться приближенной формулой
можно
воспользоваться приближенной формулой![]() .На
практике пуассоновским приближением
пользуются при npq=
np(1-p)
< 9. Исследуем
точность асимптотической формулы
Пуассона на следующем примере.ПРИМЕР
1.
Точность
формулы Пуассона.В
здании 1000 лампочек. Вероятность выхода
из строя одной лампочки в течение года
p =0.003.
Найдем вероятность того, что в течение
одного года выйдет из строя более трех
ламп. Выполним вычисления используя
формулу Бернулли и по теореме Пуассона.
Для вычисления вероятности по формуле
Бернулли используем формулу P(
> 3) = 1- P(
.На
практике пуассоновским приближением
пользуются при npq=
np(1-p)
< 9. Исследуем
точность асимптотической формулы
Пуассона на следующем примере.ПРИМЕР
1.
Точность
формулы Пуассона.В
здании 1000 лампочек. Вероятность выхода
из строя одной лампочки в течение года
p =0.003.
Найдем вероятность того, что в течение
одного года выйдет из строя более трех
ламп. Выполним вычисления используя
формулу Бернулли и по теореме Пуассона.
Для вычисления вероятности по формуле
Бернулли используем формулу P(
> 3) = 1- P(
![]() 3)
= 1- F
(3), где F
(x)
- функция распределения для биномиального
распределения. Для вычисления вероятности
по теореме Пуассона используем формулу
P(
> 3) = 1- P(
3)
= 1- F (3),
где F (x)
- функция распределения Пуассона с
параметром = np
= 3.
Выполним те
же вычисления для p
= 0.3 и n
= 10 ( = np
=3).
3)
= 1- F
(3), где F
(x)
- функция распределения для биномиального
распределения. Для вычисления вероятности
по теореме Пуассона используем формулу
P(
> 3) = 1- P(
3)
= 1- F (3),
где F (x)
- функция распределения Пуассона с
параметром = np
= 3.
Выполним те
же вычисления для p
= 0.3 и n
= 10 ( = np
=3).
28.
Стьюдента
распределение с
f
степенями свободы, распределение
отношения Т
= X/Y
независимых случайных величин Х
и Y,
где Х
подчиняется нормальному
распределению
с математическим ожиданием EX
= 0 и дисперсией DX
= 1, а fY2
имеет «Хи-квадрат»
распределение
с f
степенями свободы. Функция распределения
Стьюдента выражается интегралом
![]() .Если
X1,...,
Xn —
независимые случайные величины, одинаково
нормально распределённые, причём EXi
=
a и DXi=
s2
(i
=
1,..., n),
то при любых действительных значениях
а
и s
> 0 отношение
.Если
X1,...,
Xn —
независимые случайные величины, одинаково
нормально распределённые, причём EXi
=
a и DXi=
s2
(i
=
1,..., n),
то при любых действительных значениях
а
и s
> 0 отношение![]() подчиняется Стьюдента
распределение
с f =
п-1 степенями
свободы (здесь
подчиняется Стьюдента
распределение
с f =
п-1 степенями
свободы (здесь
![]() и
и
![]() ).
Это свойство было впервые (1908) использовано
для решения важной задачи классической
теории ошибок У. Госсетом (Англия),
писавшим под псевдонимом Стьюдент
(Student). Суть этой задачи заключается в
проверке гипотезы а
= a0
(a0
= заданное число, дисперсия s2
предполагается неизвестной). Гипотезу
а
=a0
считают не противоречащей результатам
наблюдений X1,...,
Xn,
если справедливо неравенство
).
Это свойство было впервые (1908) использовано
для решения важной задачи классической
теории ошибок У. Госсетом (Англия),
писавшим под псевдонимом Стьюдент
(Student). Суть этой задачи заключается в
проверке гипотезы а
= a0
(a0
= заданное число, дисперсия s2
предполагается неизвестной). Гипотезу
а
=a0
считают не противоречащей результатам
наблюдений X1,...,
Xn,
если справедливо неравенство
![]() ,
в противном случае гипотеза а
=
а0
отвергается (так называемый критерий
Стьюдента). Критическое значение t
= tn-1(a)
представляет
собой решение уравнения Sn-1(t)
= 1 –
,
в противном случае гипотеза а
=
а0
отвергается (так называемый критерий
Стьюдента). Критическое значение t
= tn-1(a)
представляет
собой решение уравнения Sn-1(t)
= 1 –![]() ,
,![]() a
— заданный
значимости
уровень
(0 < a <
a
— заданный
значимости
уровень
(0 < a <
![]() ).
Если проверяемая гипотеза а
= а0
верна, то критерий Стьюдента, соответствующий
критическому значению tn–1(a),
может её ошибочно отвергнуть с вероятностью
а.Стьюдента
распределение
используется для решения множества др.
задач математической статистики (см.
Малые
выборки,
Ошибок
теория,
Наименьших
квадратов метод)Критерий
Пирсона
).
Если проверяемая гипотеза а
= а0
верна, то критерий Стьюдента, соответствующий
критическому значению tn–1(a),
может её ошибочно отвергнуть с вероятностью
а.Стьюдента
распределение
используется для решения множества др.
задач математической статистики (см.
Малые
выборки,
Ошибок
теория,
Наименьших
квадратов метод)Критерий
Пирсона
|
|
|
|
Нормальный закон распределения характеризуется плотностью вероятности вида где M{X}, ____ — соответственно математическое ожидание и дисперсия случайной величины. согласованности изучаемого распределения с нормальным
Для проверки гипотезы о соответствии, экспериментального закона распределения случайной величины нормальному применяют критерий Пирсона или, как его иначе называют, критерий X2 (хи-квадрат),так как принятие и отклонение гипотезы основаны на X2 -распределении.
Использование критерия Пирсона основано на сравнении эмпирических (наблюдаемых) ___ и теоретических (вычисленных в предположении нормального распределения) _____ частот. Обычно ____ и _____ различны.
Возможно, что расхождение случайно (незначимо) и объясняется малым числом наблюдений, способом их группировки Или другими причинами. Возможно, что расхождение частот неслучайно (значимо) и объясняется тем, что теоретические частоты вычислены, исходя из неверной гипотезы о нормальном распределении генеральной совокупности.Критерий Пирсона отвечает на поставленный ранее вопрос. Однако, как и любой статистический критерий, он не доказывает справедливость гипотезы, а лишь устанавливает при принятом уровне значимости q ее согласие или несогласие с данными наблюдений.Пусть по выборке объема ___ получено эмпирическое распределение.
Допустим, в предположении нормального распределения генеральной совокупности, вычислены теоретические частоты _____. При уровне значимости q требуется проверить нулевую гипотезу: генеральная совокупность распределена нормально.В качестве критерия проверки нулевой гипотезы принимается случайная величина илигде К- число интервалов (вариант).Эта величина случайная, так как в различая опытах она принимает различные, заранее неизвестные значения. Чем меньше различаются эмпирические и теоретические частоты, тем меньше значение критерия (1.9) и, следовательно, он в известной мере характеризует близость эмпирического и теоретического распределений. Возведением в квадрат разностей частот устраняется возможность взаимного погашения положительных и отрицательных разностей.При неограниченном возрастании объема выборки ( _________ ) закон распределения случайной величины (1.9), независимо от того, какому закону распределения подчинена генеральная совокупность, стремится к закону распределения X2 с f степенями свободы. Поэтому случайная величина (1.9) обозначена X2, а сам критерий называют критерием согласия "хи квадрат".
Число степеней свободы находят по равенству f=K-1-l где l- число параметров предполагаемого распределения, которые оценены по данным выборки, а l вызвана тем, что имеется дополнительное ограничение:т.е.- Теоретическое число элементов совокупности должно быть равно фактическому числу элементов.
Поскольку в данном случае, предполагаемое распределение является нормальным, nо оценивают два параметра (математическое ожидание и среднеквадратическое отклонение), поэтому l=2 , и число степеней свободы Если расчетное (наблюдаемое) значение критерия (1.9).оказалось меньше критического _____ которое находят по таблицам, для соответствующего уровня значимости q и числа степеней свободы , т.е. если то нет оснований отвергнуть нулевую гипотезу о нормальности распределения. В противном случае (при ___________ ) нулевая гипотеза отвергается.
При проверке гипотезы о нормальности распределения существует правило, согласно которому общее количество элементов выборки должно быть а число элементов, попавших в любой i-и интервал (т.е. значения эмпирических частот ____),должно быть ___________________________
Если в крайние интервалы попадает меньшее число элементов, то они объединяются с соседними интервалами. Внутренние интервалы объединять запрещается. Общее число интервалов К , оставшихся после объединения, должно удовлетворять условию _____________ Иначе число степеней, свободы f окажется равным нулю, и гипотезу невозможно будет проверить.В целях контроля вычислений формулу целесообразно преобразовать к виду приведен пример расчета наблюдаемого значения критерия ____ по известным эмпирическим и теоретическим частотам. Если _________ , то нет оснований отвергнуть нулевую гипотезу. Т.е., расхождение эмпирических и теоретических частот незначимо. Следовательно, данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.
