1. Симплекс-метод

Розглянемо на прикладі розв’язок загальної задачі лінійного програмування данним універсальним методом.

Цементний завод відвантажує тарований (у мішках) цемент з трьох вантажних фронтів, що знаходяться в різних районах заводу. Кожен вантажний фронт має визначену місткість вагонів. Маневрові і вантажні операції виконує ОХВДТ, що одержує за це визначену плату.

Розміщення по фронтах і прибирання вагонів виконує один локомотив із тривалістю 22 години на добу. Оскільки вантажні фронти знаходяться в різних районах, витрати локомотиво-годин на маневрову роботу, що приходиться на один вагон, для кожного вантажного фронту різні. Різний і доход ОХДЩТ від навантаження на різних фронтах унаслідок різної продуктивності навантажувальної техніки.

Необхідно зробити відвантаження маршруту з 60 вагонів, що подані на заводську станцію. Як потрібно розставити вагони по фронтах, щоб забезпечити максимальне добове навантаження й одержати максимальний доход? Вихідні дані і характеристики фронтів зведені в табл. 1.

Вантажний фронт	Місткість вагонів	Витрати локомотиво-годин на один вагон	Доход, грн.ваг.
1	20	0,4	2
2	30	0,2	4
3	25	0,3	3

Відповідь на поставлене запитання дає строгий тематичний розв’язок. Спочатку сформулюємо поставлену задачу.

Позначимо число вагонів, призначених для навантаження на вантажному фронті 1 – Х₁, на фронті 2 – Х₂ і фронті 3 – Х₃. Умовна функція, що виражає загальний доход ОХЯЗДТ від навантаження вагонів, у цьому випадку запишеться в такий спосіб:

З = 2Х₁ + 4Х₂ + 3Х₃. (1)

Але на аргументи цієї функції накладено обмеження. Складаємо їх:

1) насамперед, необхідно врахувати, що сума поданих вагонів не повинна перевищувати їхнього числа,тобто

Х₁ +Х₂ + Х₃  60;

2) далі, загальний час на маневрові операції по перестановці вагонів по фронтах не повинен перевищувати ресурс локомотиво-годин,тобто

0,4Х₁ + 0,2Х₂ + 0,3Х₃ 22;

3) місткість вантажних фронтів теж обмежена

Х₁  20; Х₂  30; Х₃  25.

Таким чином, постановка задачі така: необхідно визначити ненегативні значення аргументів, що обертають у максимум лінійну функцію

З = 2Х₁ + 4Х₂ + 3Х₃  max (2)

зв'язаних системою лінійних обмежень

х₁ + х₂ + х₃  60

0,4х₁ + 0,2х₂ + 0,3х₃  22

х₁  20 (3)

х₂  30

х₃  25

Іншими словами, із усіх можливих розв’язків системи нерівностей (3) необхідно вибрати такий, котрий відповідає максимальному значенню цільової функції (2).

Якщо ввести додаткові невідомі у₁ - число не поданих під вивантаження вагонів, у₂ - кількість невикористаних локомотиво-годин, у₃, у₄, у₅ - невикористання місткості вантажних фронтів, одже систему лінійних нерівностей (3) можна записати у виді системи лінійних рівнянь:

х ₁ + х₂ + х₃ + у₁  60

0,4х₁ + 0,2х₂ + 0,3х₃ + у₂  22

х₁ + у₃  20 (4)

х₂ + у₄  30

х₃ + у₅ 25

Оскільки число невідомих (вісім) більше числа рівнянь (п'ять), то дана система невизначена, з незліченою безліччю розв’язків. Невизначені системи розв’язують у такий спосіб.

Усі невідомі довільно підрозділяють на базисні і вільні. Число базисних визначається числом лінійно незалежних рівнянь. Інші невідомі будуть вільні. До них додають довільні значення і підставляють у систему, що при цьому з невизначеної перетворюється у визначену з єдиним розв’язком. До будь-якого набору вільних невідомих можна додати безліч довільних значень, що дадуть безліч розв’язків системи (4). Якщо усі вільні невідомі дорівняти нулеві (як окремий випадок), то розв’язок буде складатися тільки зі значень базисних невідомих. Такий розв’язок називається базисним.

Розглядаючи в якості вільних будь-які інші невідомі, можна одержати різні базисні розв’язки, число яких визначається числом сполучень з n пo m елементів , де n-загальне число невідомих; m - число базисних невідомих.

Серед базисних розв’язків системи завжди можна знайти оптимальний, а в деяких випадках і кілька оптимальних, але усі вони забезпечать екстремум цільової функції.

Таким чином, якщо знайти який-небудь базисний план, а потім поліпшувати його, то зрештою вийде оптимальний розв’язок.

На цьому принципі і побудований сімплекс-метод.

У нашому випадку зручно знайти базисний план, прийнявши в якості базисних п'ять невідомих (за числом рівнянь) у₁, у₂, у₃,у₄, у₅. Тоді вільними невідомими будуть х₁, х₂, х₃.

В икористовуючи систему (4), виразимо всі базисні невідомі через вільні:

у₁ = 60 – (х₁ + х₂ + х₃)

у₂ = 22 – (0,4х₁ + 0,2х₂ + 0,3х₃)

у₃ = 20 – х₁ , (5)

у₄ = 30 – х₂

у₅ = 25 – х₃

Виразимо і цільову функцію в аналогічній формі:

С = 0 – (-2х₁ – 4х₂ – 3х₃). (6)

Дорівнявши вільні невідомі нулеві, одержимо такий базисний план

у₁ = 60, у₂ = 22, у₃ = 20, у₄ = 30, у₅ = 25.

Назвемо його початковим. Він відповідає ситуації, коли вагони взагалі не подають під навантаження, а загальний доход ОХЖДТ (значення умовної функції С) дорівнює нулеві.

Початковий план необхідно поліпшити, тобто перейти до іншого базисного плану. Базисні плани відрізняються один від одного набором вільних і базисів невідомих. Виходить, якщо виключити яку-небудь невідому з числа базисних і ввести її в число вільних, а з числа вільних одне невідому ввести в число базисних, одержимо новий базисний план. Необхідно лише знайти такі невідомі, за яких наступний базисний план буде кращим, ніж попередній, тобто збільшить значення цільової функції С. Ці дії і виконують за допомогою симплекс-методу.

У першу симплекс-таблицю (табл. 1) вносять дані початкового плану, тобто записують усі коефіцієнти при вільних невідомих (зі знаком у круглих дужках системи (5) у відповідних стовпцях і вільні члени системи (5) в останньому стовпці, що позначено одиницею). Перший рядок відповідає виразу у₁ , друга – у₂ і т.д. В останньому рядку С записують коефіцієнти при невідомих цільових функціях. Остання клітка цього рядка призначена для запису значення цільової функції (її вільного члена), що у даному випадку (при х₁=х₂=х₃=0) дорівнює нулеві. Таким чином, кожен рядок таблиці, що називається матрицею, позначається відповідною базисною невідомою і знаком цільової функції С, кожен стовпець - вільної невідомої зі знаком мінус і одиницею (для вільних членів). Знак мінус перед вільною невідомою відповідає мінусові, що стоїть перед круглими дужками у виразах (5) і (6). Тому що в базисному плані значення вільних невідомих дорівнює нулеві, то всі значення базисних невідомих рівні відповідним вільним членам. Отже, у розглянутому базисному плані (див. табл. 1)

у₁=60; у₂=22; у₃=20; у₄=30; у₅=25.

Щоб замінити перемінні, потрібно спочатку їх вибрати, а потім поміняти місцями. У результаті буде отримана нова матриця з новим планом. Усе це виконується за допомогою симплекс-методу, алгоритм якого полягає в наступному:

1. Вибір розв’язуючого елемента.

1.1. Стовпець, що містить найбільший за абсолютною величиною негативний елемент С - рядка, приймається як дозволяюча.

1.2. Розглядають усі позитивні елементи дозволяючого стовпця, (крім елемента С - рядка) і на них поділяють відповідні вільні члени. Мінімальне з отриманих відносин визначає розв’язуючий рядок. На перетині розв’язуючого рядка і стовпця знаходиться розв’язуючий елемент. Якщо виявиться два або більше однакових найбільших за абсолютною величиною негативних елементів С - рядка, то як розв’язуючий стовпець вибирають той, котрому відповідає максимальне з двох мінімальних відношень.

2. Складання нової матриці, модифіковані Жорданові виключення.

2.1. У новій матриці елемент, що стоїть на місці елемента попередньої розв’язуючої матриці, визначається розподілом одиниці на розв’язуючий елемент:

де a_rs - елемент попередньої дозволяючої матриці розташований на перетині розв’язуючого рядка r і стовпця S.

2.2. Інші елементи, що стоять на місці розв’язуючого рядка, визначають розподілом відповідних елементів попередньої матриці на розв’язуючий елемент

де a_rj - елемент рядка попередньої розв’язуючої матриці.

2.3. Інші елементи, що стоять на місці дозволяючого стовпця, визначають аналогічно, але міняють знак на протилежний

де a_is - елемент стовпця розв’язуючої матриці.

Всі інші елементи нової матриці визначають за формулою

де a_ij - відповідний елемент попередньої матриці; a_is - елемент попередньої матриці, що стоїть на перетині рядка і розглянутого елемента і дозвільного стовпця a_rj - елемент попередньої матриці, що стоїть на перетинанні розв’язуючого рядка і стовпця в розглянутому елементі.

Усі перелічені дії становлять одну ітерацію (поліпшення), у результаті якої відбувається перехід від одного базисного плану до іншого, поліпшеного. Ітерації повторюються доти, поки не буде отримано план, що уже не можна поліпшити. Цей план і буде оптимальним. Ознака оптимальності плану (тобто неможливості його поліпшення) - відсутність у С - рядка негативних елементів.

У першій симплекс-таблиці (див. табл. 1) найбільший за абсолютною величиною негативний елемент С - рядка розташований у стовпці (-х₂) і дорівнює 4. Вибираємо його в якості розв’язуючого. Це означає, що невідому х₂ треба виключити з числа вільних і включити в число базисних, а з числа базисних треба перевести одне невідоме в число вільних. Для цього треба вибрати розв’язуючу сторону, (п. 1.2 алгоритму). Поділяємо вільні члени рядків базисних невідомих на відповідні позитивні елементи розв’язучого стовпця (-х₂):

Рядок (у₄), що відповідає мінімальному відношенню (30), приймаємо в якості дозволяючого. На перетині дозволяючих стовпця (-х₂) і рядка (у₄) знаходиться розв’язуючий елемент (узятий у рамку). Далі формуємо нову матрицю (табл. 2) за пунктами частини 2 алгоритми.

1. Елемент, що стоїть на місці розв’язуючого (r=4; S=2) , переноситься в нову матрицю без зміни, оскільки він дорівнює одиниці.

2. Інші елементи розв’язуючого рядка також зберігають свої значення (розподіл на одиницю).

3. Інші елементи розв’язуючого стовпця (крім розв’язуючого елемента) зберігають свої значення (розподіл на одиницю), але змінюють знак на протилежний.

4. Визначаємо інші елементи нової матриці. Елемент, що стоїть на перетині перших рядка (i=1) і стовпця (j=1)

і так далі.

Для полегшення обчислень використовують таке правило. Щоб визначити який-небудь елемент нової матриці (не приналежний розв’язуючему рядку і стовпцю), необхідно відповідний йому елемент старої матриці і її розв’язуючий елемент об'єднати прямокутним контуром. Різниця добутків протилежних вершин контуру - чисельник формули для визначення b_il поділяємо на розв’язуючий елемент. Наприклад, для останнього елемента першого рядка (вільний член виразу в₁) будуємо прямокутний контур (штрихова лінія) на матриці.

Таблиця 1

Початковий план

3 Таблиця

Таблиця 4

Таблиця 2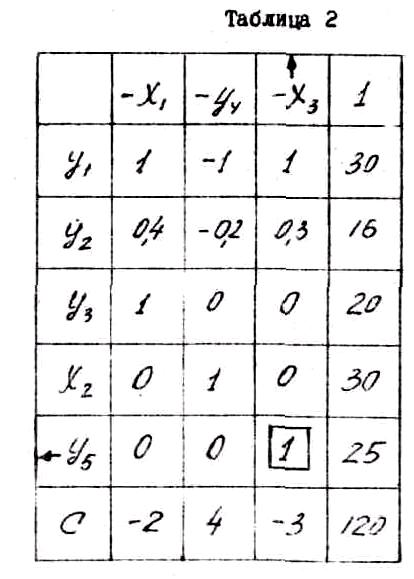

Аналогічно обчислюємо всі інші елементи матриці, включаючи й елементи С - рядка. У результаті одержуємо новий базисний план (див. табл. 2) зі зрослим значенням цільової функції С=120 новими значеннями базисних невідомих у₁=30; у₂=16; у₃=20; х₂=30; у₅=25. Сутність даної ітерації можна пояснити, тільки розв’язавши систему лінійних рівнянь. Симплекс-метод дозволяє перехід від однієї симплекс-таблиці до іншої, поліпшувати базисні плани, не виконуючи ніяких дій із системами лінійних рівнянь. Результати подальших поліпшень базисних планів приведені в табл. 3 і 1.