§ 3.7. Основные свойства z-преобразования

Для z-преобразования справедливы некоторые теоремы, аналогичные теоремам о спектрах непрерывных сигналов. Главная из них — теорема о свертке.

Теорема о свертке. В теории непрерывных сигналов эта теорема формулируется следующим образом. Пустьзаданы два непрерывных сигнала x(t) и y(t) и их свертка

Тогда спектральная плотность свертки связана со спектральными плотностями и сигналов x(t) и y(t) соотношением

(3.23)

Для дискретных сигналов x_k = x(kT) и y_k = y(kT] по аналогии с непрерывными сигналами вводится дискретная свертка, которая определяется выражением

(3.24)

или

(3.25)

Запишем для дискретных сигналов , и их z-преобразования

Применим z-преобразование к формуле свертки (3.25)

Преобразуем правую часть этого выражения так, чтобы получить произведение z-преобразований. Для этого нужно, в частности, чтобы x_k умножалось на , а на . Сгруппируем соответствующим образом степени z:

При k> n , поэтому можно во второй сумме верхний предел суммирования сделать равным ∞. Далее обозначим п — k = т и получим

Нижний предел m=— k можно заменить на m = 0 так как при m<0 все y_m = 0. В результате получим

т.е.

(3.26)

Выражение (3.26) аналогично формуле (3.23), описывающей теорему о свертке для обычных непрерывных сигналов.

В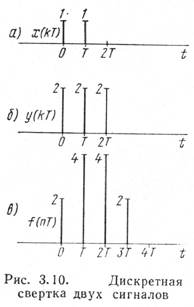качестве примера рассмотримдискретную свертку двух простых сигналов: x(kT), имеющего два не­нулевых отсчета [x(0)=1 и х(Т) =1] (рис. 3.10, а) и y(kT), состоящего из трех отсчетов [у(0) = 2; у(Т) = 2; у(2Т) = 2] (рис. 3.10,6). Непосредственный подсчет по формуле (3.24) приводит к следующему результату:

_f()

Сигнал f(nT), являющийся сверткой x(kT) и y(kT), изображен на рис. 3.10, в

Найдем z-преобразования сигналов x(kT), y(kT) и f(nT):

Перемножая выражения для X(z) и Y(z), нетрудно убедиться в справедливости выражения (3.26).

Теорема о запаздывании.

Сдвинем дискретный сигнал х(пТ) по времени на величину периода повторения Т. Полу­чившийся новый сигнал у(пТ) (рис. 3.11) связан с х(пТ) простым соотношением

Пусть известно z-преобразование сигналаx(nT):

Найдем z-преобразование сигнала у(пТ):

Таким образом, запаздывание дискретного сигнала на один элементcоответствует умножениюz-преобразованияна

Теорема Парсеваля для дискретных сигналов. Как известно, энергия непрерывного сигнала может быть вычислена посредством интегрирования в бесконечных пределах или квадрата временной функции, или квадрата ее спектра. Аналитически это записывают в виде теоремы Парсеваля:

Аналогичное соотношение можно получить для дискретных сигналов.

Пусть дискретный сигнал f(kТ) представляет собой убывающую последовательность, так что все полюсы его z-преобразования F(z) находятся внутри единичной окружности в плоскости z. Для вывода теоремы Парсеваля умножим F(z) на F(l/z) и найдем величину этого произведения:

(3.27)

Умножим обе части равенства (3.27) и и проинтегрируем по замкнутому контуру L, который должен располагаться в области сходимости как F(z), так и F(l/z). Поскольку последовательность f(kT) является убывающей, в качестве контура интегрирования L можно принять окружность | z | = 1. При интегрировании двойной суммы в правой части равенства (3.27) все члены окажутся равными нулю, кроме членов, соответствующих k = п. В результате получим

(3.28)

Выражение (3.28) является записью теоремы Парсеваля для дискретных сигналов.