Книга по вейвлетам / glava21

Глава 2

Гармонический (частотный) анализ

В математике и физике еще в работах Л. Эйлера и Ж.Л. Лагранжа в 18

веке широкое распространение получил метод разложения периодических функций в ряды по синусам и косинусам, названные тригонометрическими рядами. В 19 веке французский математик и физик Ж. Фурье впервые сформулировал основные требования к функциям, представляемым такими рядами, обеспечивающими их сходимость, заложив основы гармоническо-

го анализа. В дальнейшем теория гармонического анализа была развита в работах Дирихле, Гаусса, Римана, Чебышева, Винера, Пэли и других. В ча-

стности, гармонический анализ периодических функций был распростра-

нен на функции с бесконечным периодом, получивший название интегра-

ла Фурье.

Впоследствии теория преобразования Фурье периодических и непе-

риодических функций вышла далеко за пределы математических дисцип-

лин, став мощной теоретической базой в ряде прикладных областей, таких как радиоэлектроника и радиотехника, теория систем, теория автоматиче-

ского регулирования, теория сигналов и др.

58

2.1. Ряды Фурье

Рядом Фурье может быть представлена периодическая функция f (t) = f (t + nT ), n Z , удовлетворяющая условиям Дирихле: ограничен-

ность, кусочная непрерывность (разрывы первого рода), конечное число экстремальных значений на периоде (ограниченная вариация), в любой точке периода конечность производной от функции, или хотя бы, правой или левой производной (условие Дини).

Если перечисленные условия удовлетворяются, то в соответствии с

	(1.34а) функция f (t) может быть представлена рядом
		∞				t
	f (t) = ∑F[k]e j2πk						,
						T				(2.1.1а)
	k=−∞
	где F[k] вычисляется по (1.34б):
	F[k]=	1		T / 2	f (t)e− j2πk			t
				∫					dt .
								T		(2.1.1б)
		T
				−T / 2

Обратим внимание, что в основу рядов Фурье положена ортогональ-

	ная система функций {ϕk (t)}:
		(t) = e	j2πk	t
	ϕk			T
	для t [− T/2,T/2] и k Z .

Легко проверить, что

ϕk (t),ϕl (t)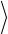 = Eϕδ [l − k],

где Eϕ = T , так как
T / 2	j2π (l−k )	t		T
∫ e		T dt =		π (l − k )	sin(π (l − k )).
−T / 2

59

Формула (2.1.1б) определяет коэффициенты разложения (2.1.1а) един- ственным образом. Если f (t) непрерывна, то ряд (2.1.1а) сходится равно- мерно к f (t). Если f (t) квадратично интегрируема, но необязательно не- прерывна, то ряд сходится к f (t) в смысле L2 . Это означает, что ошибка f (t)− fˆN (t) должна стремиться к нулю при N → ∞, где fˆN (t) обозначен

усеченный ряд (2.1.1а) для k , изменяющемся от − N до N . В точках раз- рыва предел суммы (2.1.1а) равен среднему (f (t + )+ f (t − ))2 . Однако схо- димость в этой точке неравномерная, значение fˆN (t) будет колебаться

вблизи точки разрыва (явление Гиббса). Величина колебаний зависит от величины N .

Соотношение Парсеваля (1.29) – скалярное произведение двух про- извольных периодических функций f (t) и g(t), удовлетворяющих усло-

вию Дирихле, вычисленное по одному периоду, равно:

f (t),g(t)[−T / 2,T / 2] = T F(k ),G(k ) .

В частности, для g(t) = f (t)

f (t) 2[−T / 2,T / 2] = T F (k ) 2 ,

где

f (t) = f , f = ∫ f (t)2dt .

T

Можно показать, что коэффициенты F[k], вычисленные по (2.1.1б)

обеспечивают наилучшее приближение рядом (2.1.1а), т.е. всегда ошибка аппроксимации рядом (2.1.1б) меньше ошибки аппроксимации любым другим рядом:

N			N
f (t)− ∑ ϕk , f ϕk	(t)	≤	f (t)− ∑akϕk	(t)	,
k =− N			k=−N

где {ak } – произвольное множество коэффициентов.

60

Действительно, запишем правую часть неравенства в виде выражения

f (t) 2 − 2T ak , F[k] + T ak 2 ,

которое после преобразования с учетом (2.1.1б) будет иметь вид:

f (t) 2 − T F[k] 2 + T ak − F[k] 2 .

Очевидно, что это выражение и, следовательно, ошибка аппроксима-

	ции, минимальны, если ak = F[k].
	В заключение отметим, что, заменяя переменную t в (2.1.1) на t =					Tx	,
						2π
	получим пару преобразований уже для 2π -периодической функции f (x):
	F[k]=	1		π
				∫ f (x)e− jkxdx ,	(2.1.2а)
			2π
				−π
				∞
	f (x)	= ∑F[k]e jkx .			(2.1.2.б)

k=−∞

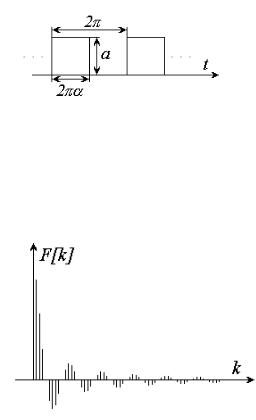
Рис. 2.1а.

Прямоугольный периодический импульс (α < 1)

Рис. 2.1б.

Дискретный спектр Фурье прямоугольного импульса (рис. 2.1а)

Последние выражения носят более общий характер, так как не зависят от величины периода T .

Рассмотрим несколько примеров преобразования Фурье периодических функций.

Пример 2.1.

Найти коэффициенты ряда Фурье прямоугольного импульса (рис. 2.1а)

Имеем из (2.1.2а)

F[k] =	a	πα	a		e jπkα − e− jπkα		sinπ kα
		∫ e− jkxdx =				= aα		.
	2π		πk		2 j
		−πα					π kα

61

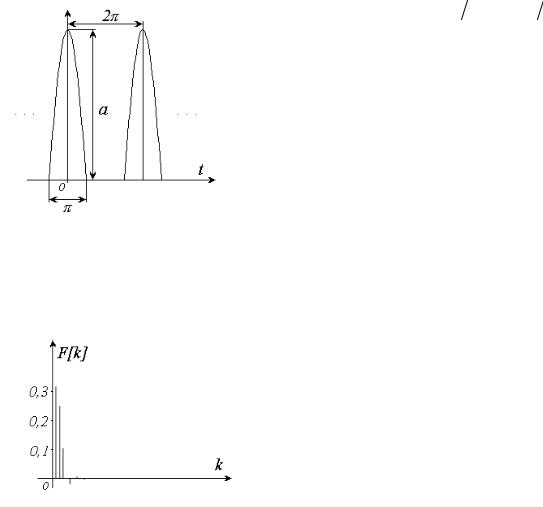
Дискретный спектр показан на рис. 2.1б.

Пример 2.2.

Найти коэффициенты ряда Фурье функции (рис. 2.2а):

Рис. 2.2а.

Периодическая функция "полуволна косинусоиды"

Рис. 2.2б.

Дискретный спектр Фурье "полуволны косинусоиды"

(рис. 2.2а).

f (x) = a cos x

для

−π 2 ≤ x ≤ π 2 .

Имеем из (2.1.2а):

F[k]=

a

π

/ 2

− jk x

∫ cos x e

dx =

2π

−π / 2

a

π / 2

π / 2

=

∫ e jxe− jkxdx +

∫ e− jxe− jkxdx =

4π

−π / 2

−π / 2

π

[k −1]

sin

π

(k

a

sin

2

2

+1)

=

+

.

2π

k −1

k +1

Отсюда

F[0] =

a

, F[±1] =

a

, F[2n −1] = 0

π

4

и

F[2n] =

π

(2n

−1)

π

(2n +1)

a

sin

sin

=

2

+

2

,

2π

2n +1

2n −1

для

n = ±1, ± 2, ± 3, K

Дискретный спектр функции этого примера показан на рис. 2.2б.

62

2.2. Интеграл Фурье

Интеграл Фурье – это, по существу, непрерывное представление сиг-

налов, рассмотренное в п. 1.7 в классическом базисе Фурье. В этом случае сигнал рассматривается как функция, заданная на бесконечном интервале.

Чтобы получить выражения, аналогичные (1.46), подставим (2.1.1б) в (2.1.1а). Получим

1

∞

T / 2

f (t) =

∑

∫

f

(τ )e− jkω0 τ dτ e jkω0 t ,

T

k=−∞ −T / 2

где

ω0

=

2π

.

T

Так как T =

2π

,

ω0

1

∞

T / 2

f (t) =

∫

f (τ )e− jkω0τ dτ e jkω0tω

0 .

2π

∑

k=−∞ −T / 2

При T → ∞, ω0 → dω , kω0 = ω сумма превращается в интеграл

1

∞

f (t) =

∫ F(ω)e jω t dω ,

(2.2.1а)

2π

−∞

где

∞

F(ω ) = ∫ f (t)e− jω t dt =

e− jω t , f (t)

t .

(2.2.1б)

−∞

Интеграл (2.2.1б) называется прямым, а (2.2.1а) – обратным преобра- зованием Фурье. Комплексная функция F (ω ) имеет смысл спектральной

плотности, ее иногда называют непрерывным спектром Фурье-функции f (t).

Также как и в случае периодической функции, предполагается, что f (t) удовлетворяет условиям Дирихле или, что эквивалентно, абсолютно

63

интегрируема и удовлетворяет условию Дини. Тогда, если функция f (t) непрерывна, то обратное преобразование (2.2.1а) точно равно f (t). Если f (t) квадратично интегрируема, то обратное преобразование Фурье спра-

ведливо в среднеквадратическом (в смысле L2 ), т.е. норма f (t)− fˆ (t) ≈ 0 .

Допуская, что прямое и обратное преобразования Фурье существуют,

введем обозначение пары Фурье-преобразования:

f (t) ↔ F(ω ).

Отметим также, что

F (−ω) = F(ω), F(−ω ) = F (ω ) и f (t) ↔ F (−ω ),

так как

		1	∞	1	∞
	f (t) =		∫ F (ω)e− jωt dω =		∫ F (−ω )e jωt dω .
		2π		2π
			−∞		−∞

Преобразование Фурье обладает рядом замечательных свойств.

Линейность. Следует из свойств линейности скалярного произведе-

ния. Для постоянных α и β имеем:
α f (t)+ β g(t) ↔ α F(ω)+ β G(ω ).	(2.2.2)
Симметрия.
F(t) ↔ 2πf (−ω),	(2.2.3)

которая следует из (2.2.1б) после замены ω на t и сравнения полученного

	выражения с (2.2.1а):
	∞		1	∞
	F(t) = ∫	f (ω)e− jω t dω =		∫ 2πf (−ω )e jω t dω .
			2π
	−∞			−∞
	Сдвиг. Сдвиг во временной области на t0				приводит к умножению на
	фазовый коэффициент в Фурье области
	f (t − t0 ) ↔ e− jω t0 F(ω).				(2.2.4а)

64

на вещественную константу

И наоборот, сдвиг в частотной области приводит к модуляции ком-

плексной экспоненты во временной области

e jω0t f (t) ↔ F(ω −ω0 ).

(2.2.4б)

Масштабирование. Умножение переменной t во временной области

α приводит к делению на эту константу пе-

ременной ω в частотной области, как следует из пары преобразований:

f (α t) ↔		1		F	ω	.	(2.2.5)
		α			α

Дифференцирование/интегрирование. Определим спектр производ-

ной f ′(t). Из (2.2.1б) получим, интегрируя по частям:

∞		∞	∞
∫ f ' (t)e− jω t dt = f (t)e− jω t			+ jω ∫ f (t)e− jω t dt .
−∞		− ∞	−∞

Так как функция, представимая интегралом Фурье, обращается в нуль

при t = ±∞ , то, следовательно, имеем пару

df (t) ↔ jωF(ω). dt

В случае n -ой производной

d n f (t)

n

↔ ( jω) F

(ω).

dtn

f (t) получим,

Для спектра Фурье интеграла от функции

по частям

∞

t

1

∞

F(ω )

∫

e

− jω t

∫

f (τ )dτ dt =

∫

f (t)e− jω t dt =

.

jω

jω

−∞

−∞

−∞

Следовательно,

∫ f (τ )dτ ↔ F(ω).
t
−∞	jω

(2.2.6)

интегрируя

(2.2.7)

65

Дифференцирование в частотной области дает

	(− jt)n f (t) ↔		d n F(ω )				.	(2.2.8)
			dω n
	Теорема моментов. Начальный момент n -го порядка (В.2) может
	быть определен как
	n	d n F(ω)
	(− j) mn =					.		(2.2.9)
		dω n
						ω = 0
	Теорема о свертке. Спектр свертки функций							f (t) и g(t) определяется
	из соотношения
	f (t) g(t) ↔ F (ω )G(ω) ,							(2.2.10)

где знак ( ) означает свертку двух функций.

Для доказательства рассмотрим свертку двух функций из L1 (R)

∞

f (t) g(t) = ∫ f (τ )g(t −τ )dτ

−∞

и выполним ее преобразование Фурье

∞	∞			∞	f (τ )e− jωτ G(ω)dτ = F(ω )G(ω ).
∫	f (τ )	g(t −τ )e− jωt dt dτ =		∫
	∫
−∞	−∞			−∞
Свертка в частотной области дает пару преобразований
			f (t)g(t) ↔	1	F(ω) G(ω),	(2.2.11)
				2π

которая носит название теоремы о модуляции.

Действительно, обратное преобразование Фурье свертки

∞

F(ω ) G(ω ) = ∫ F (ω1 )G(ω −ω1 )dω1

−∞

имеет вид:

66

1	∞		∞
	∫	F(ω )		G(ω −ω	)e jω t dω dω		=
2π
		1	∫	1		1
	−∞		−∞

∞

= ∫ F(ω1 )e jω1t g(t)dω1 = g(t) f (t).

−∞

Хорошей иллюстрацией применения приведенных выше соотношений является вывод формулы о производной свертки:

h' (t) = d[ f (t) g(t)]. dt

Фурье-преобразование h′(t) из (2.2.6) с учетом (2.2.10) равно

jω ((F(ω))G(ω )) = ( jω F (ω ))G(ω) = F(ω)( jω G(ω )).

Отсюда
h' (t) = f ' (t) g(t) = f (t) g' (t).	(2.2.12)

Эта формула широко используется для вычисления производной сиг-

нала при одновременном его сглаживании с помощью фильтра, весовая функция которого является производной известной функции, например,

гауссианы.

Формула Парсеваля утверждает, что взаимная энергия сигналов мо-

жет быть вычислена по их спектру

∞

1

∞

∫

f (t)g(t)dt =

∫ F (ω )G(ω )dω .

(2.2.13)

2π

−∞

−∞

При g(t) = f (t) имеем

∞

1

∞

∫

f (t)

2 dt =

∫

F

(ω)

2 dω .

(2.2.14)

2π

−∞

−∞

Или, в соответствии с определением нормы (1.25),

f (t)

2 =

1

F(ω )

2 .

2π

67