Линейный поиск

Рассмотрим задачу поиска элемента в одномерном массиве.

Дано:1)  число элементов массива;

2)  массив типа  array [index]  of  Elem;

3) : Elem  элемент для поиска;

4) искомый элемент в массиве есть, т. е. .

Условие 4 можно записать в виде утверждения (::) или в форме с квантором счета (:) > 0.

Найти первое вхождение в массив, т. е. найти , такое, что () & ( :: ).

Далее будем записывать утверждение ( :: ) более кратко, а именно . Тогда постутверждение для этой задачи можно записать в виде

Post: () & () & ().

Инвариант может быть получен устранением конъюнктивного члена () из постусловия Post, т. е. Inv: () & (). Если в качестве условия выхода из цикла взять устраненный конъюнктивный член (), то получим как раз требуемое: Inv & (условие выхода) Post.

Это приводит к программе вида

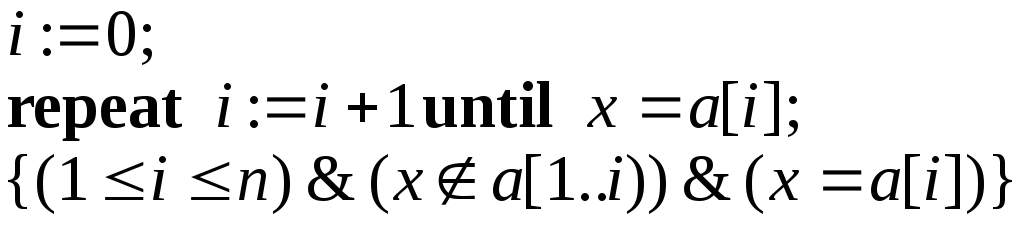
или к варианту с циклом while-do

Пусть теперь условие 4 постановки задачи не выполняется, т. е. заранее неизвестно, есть ли элемент в массиве.

Требуется: если , то установить=true  и кроме того указать , такое, что () & () & (); если (), то установить=false.

Требуемое постусловие можно записать в виде

( ), (5.1)

где введено обозначение

=(() & () & ()).

Очевидно, для решения задачи необходимо просматривать все элементы массива, пока не будет найден элемент, равный . Фактически индуктивная ф-ция над последовательностью со стационарным значением=true. Рассматривая «чтение» последовательности в естественном порядке, получим алгоритм

Инвариантом цикла здесь является утверждение () & (). Учитывая условие выхода из цикла, получаем при его завершении постутверждение (()  or ) & () & () & (), где учтено, что притело цикла выполняется хотя бы один раз. Из этого утверждения следует требуемое постусловие (5.1).

В задаче поиска с заранее неизвестным исходом удобно использовать следующий прием: добавим к массиву дополнительный элемент, играющий роль «барьера», тогда задача поиска сведется к первоначальной постановке (известно, что) и может быть решена программой

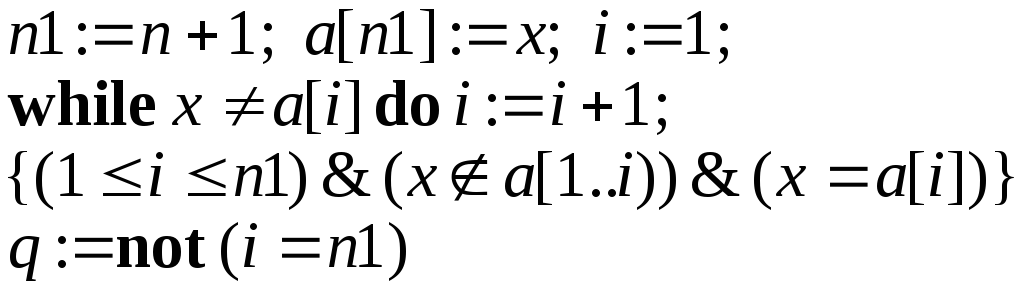
Оценивая эффективность линейного поиска по числу требуемых сравнений (или ), легко заметить, что в лучшем случае (при ) поиск завершится за один шаг, в худшем за шагов (в варианте без барьера), а в среднем за шагов (в предположении, что всеразличны и вероятность события равна ).

Билет№37 Разработка алгоритма бинарного поиска №37

Существенно лучший алгоритм, чем последовательный поиск, можно предложить в случае, когда массив упорядочен.

Дано:1) :  Integer;

2)array   of  Ordinal; Pred: (::)}

3) : Ordinal.

Требуется: либо найти индекс , определяющий место в массиве, такой, чтопри, либо указать, чтоx  a[1] или a[n] < x.

Удобно добавить «идеальные» элементы и, которые можно использовать для записи утверждений, но которые не должны входить в исполняемые инструкции программы. Тогда требуемое постутверждение примет видPost: () & (). Если такой индекс найден, то саму задачу поиска можно решить дополнительной проверкой:

что выражается постутверждением .

В качестве основной идеи алгоритма возьмем следующую: пусть сначала о локализации значения среди значенийничего неизвестно, т. е. предутверждение можно дополнить утверждением; далее при работе алгоритма будем рассматривать интервал локализации, где; причем на каждом шаге этот интервал должен уменьшаться, т. е. величинадолжна убывать. Эта идея реализуется инвариантом цикла () & () , ограничивающей функциейи условием завершения цикла. Отметим, что формально инвариант можно получить из постутверждения () заменой границ интервалаинаисоответственно. Из предусловиябудет следовать инвариант, если цикл инициализировать следующим способом:. Таким образом, имеем набросок программы, изображенной на рис. 5.1. Тело цикла должно обеспечивать уменьшение интервалапри сохранении инварианта. Очевидно, уменьшить интервал можно, выбрав значение индексавнутри интервала и сравнивс. При этомследует брать таким, чтоиеще не сравнивались, т. е.. Пусть, тогда необходимо изменить левую границу, причем так, чтобы удовлетворить инвариант, т. е., и,

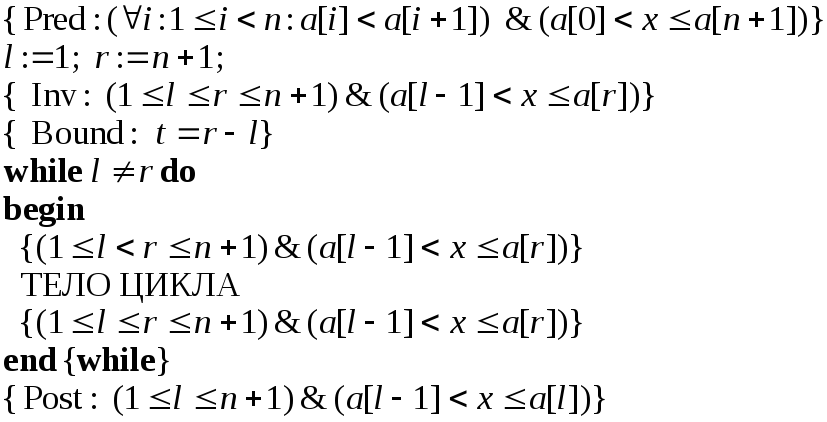
Рис.5.1. Набросок алгоритма

следовательно, . Из аналогичных соображений придолжно получаться. Таким образом, тело цикла примет вид

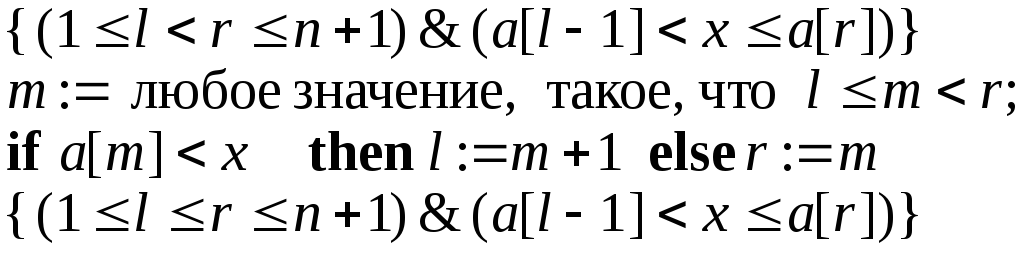
При этом действительно, при условии , верном до выполнения тела цикла, получимпосле завершения тела цикла.

Выбирая различными способами значение , получим различные алгоритмы поиска. Например, приимеем аналог линейного поиска. Здесь в случаепоиск заканчивается, а приразмер интервала уменьшается всего на 1. Ясно, что более эффективный алгоритм можно получить, выбирая значениена каждом шаге так, чтобы длина интервала уменьшалась быстрее. Идея деления интервала пополам приводит к следующему алгоритму двоичного поиска:

Отметим, что выбор значения удовлетворяет условию.

Билет№38 Разработка алгоритма бинарного поиска №38

{ Pred : (i :1 n < n : a[i+1] ) }

{Post(0  L n)&(a[L]< x  a[R])&(L=10Ln-1)&(a[L+1]=x) }

L:=0 ; R:=n+1 { a[L]<xa[R] }

While L+1<>R DO

Begin { (10  L< R-1  n) &(a[L]) < x  a[R] ) }

m=(L+R) div 2

if a[m] < x Then L:=m else R:=m

end;

{ (0  L  n) & (a[L] < a[]L+1) }

if L<>n then q:=(x=a=a[L+1] ) else q:=false

(смотри билет № 37)

Билет№39 Анализ алгор бинарного поиска №39

При разработке алгоритма бинарного поиска использовались лишь сравнения вида , где,. Определим наихудшее с точки зрения быстродействия число сравнений, требуемое алгоритмом.

Теорема 1. Максимальное число сравнений, требуемое алгоритмом бинарного поиска для нахождения места предъявленного значения среди ,есть

.

Для доказательства теоремы рассмотрим так называемое дерево бинарного поиска. Каждому сравнению в алгоритме сопоставим узел дерева и обозначим его так, как показано на рис. 5.2,а. В узле дерева (в круге) записано вычисляемое на данном шаге значение , а сверху слева и справа от него значения границ рассматриваемой части массива исоответственно. К ветвямиподвешиваются аналогичные узлы: справа для случая и слева для случая . Приузел не содержит продолжений (является листом дерева) и обозначается (рис.5.2,б) специальным образом (номером, заключенным в квадрат). Самый верхний (первый) узел называется корнем дерева. Построенное таким образом дерево описывает все возможные исходы сравнений применительно к заданным и. На рис. 5.3 изображено дерево бинарного поиска для().

Рис. 5.3. Дерево бинарного поиска для () Отметим, что в таком дереве все внутренние узлы имеют двух сыновей, поскольку на любом шаге цикла левая и правая части массива не пусты. Исходам поиска соответствуют листья дерева, пронумерованные от 1 до. Внутренние узлы содержат номера элементов массива, с которыми может сравниваться значение, т. е. все номера от 1 до. Для данныхипоследовательность сравнений, требуемых алгоритмом бинарного поиска, задает путь в дереве от корня к результирующему листу.

Определим уровень узла в дереве следующим образом: уровень корня равен нулю, уровень любого другого узла на единицу больше уровня его непосредственного предка (отца). Глубину дерева определим как значение максимального из уровней его листьев.

При получится ровное дерево с листьями только на последнем-м уровне. Например, длядерево имеет вид, изображенный на рис. 5.4,а. Очевидно, максимальное число сравнений алгоритма бинарного поиска для заданного определяется глубиной дерева бинарного поиска. Пусть, или в иной форме записи

.

Покажем, что  глубина дерева бинарного поиска в массиве из элементов. Доказательство проведем индукцией по. При= 1 имеем(), дерево изображено на рис. 5.4,б и его глубина равна 1.

Пусть для некоторого имееми глубина дерева есть(индуктивное предположение). Покажем, что приглубина дерева равна+ 1. Пустьчётно. На первом шаге алгоритма бинарного поиска перейдем к одной из двух задач: в левом поддереве с кол-ом исходов/2 либо в правом поддереве с кол-ом исходов/2. Поскольку из неравенствапри чётномследует неравенство, то с учетом индуктивного предположения получим глубину дерева+ 1. При нечётномна первом шаге задача разделится на две подзадачи: в левом поддереве с числом исходов, в правом . Поскольку из неравенствапри нечётномследуети далее, то с учётом индуктивного предположения глубина дерева равна+ 1. Теорема доказана.

Как видно, число сравнений в алгоритме равно либо (лист на последнем уровне), либо 1 (лист на предпоследнем уровне). Число листьев на этих уровнях легко определить следующим образом. Пусть или, где. Пустьи число листьев на уровнях и 1 соответственно. Тогда += общее число листьев. С другой стороны, число внутренних узлов на предпоследнем уровне равно и к каждому из них подвешены по два узла последнего уровня (листа), т. е.. Таким образом, имеем два уравнения для определенияи :

+=,,

из которых следует и.

Отсюда легко подсчитать среднее число сравнений, требуемое алгоритмом бинарного поиска, при условии, что все исходы (варианты попадания в различные интервалы) равновероятны. Действительно,

Очевидно, что , причемпри(), т. е. в случае ровного дерева.

Насколько хорош алгоритм бинарного поиска? Можно ли предложить лучший по числу сравнений алгоритм? На эти вопросы отвечает следующая теорема.

Теорема 2.  Для произвольного алгоритма поиска в массиве, использующего сравнения, можно подобрать такие исходные данные и ,что применение к ним этого алгоритма потребует не менее сравнений.

Для доказательства теоремы рассмотрим последовательности вопросов, на каждый из которых дается ответ: да или нет. Каждой такой последовательности можно сопоставить последовательность из нулей и единиц. Если применение алгоритма к исходным данным ипотребовало ровносравнений, а его применение к даннымидало тот же результат (ту же «01»-последовательность) за первые шагов, то дальнейших сравнений уже не потребуется и итог будет таким же, как и в первом случае, поскольку порожденная алгоритмом последовательность сравнений рассматриваемого вида определит один и тот же интервал локализации элементови(с точки зрения сравнения с элементами массивапредъявляемыеи«выглядят» одинаково). Следовательно, среди получающихся «01»-последовательностей: а) ни одна не является началом другой и б) нет совпадающих последовательностей, соответствующих разным интервалам локализации. Если ограничиться длиной последовательности , то всего таких последовательностей будет. Ясно также, что их должно быть не меньше, чем число исходов применения алгоритма (число распознаваемых ситуаций), т. е.и, следовательно,или, так какm  целое число, то .

Теорема доказана.

Сопоставление теорем 1 и 2 показывает, что алгоритм бинарного поиска является оптимальным (наилучшим по числу сравнений).

Билет№40 Алгоритм програм бинар поиска №40