10. Дайте определение эмпирической функции распределения. Дайте определение эмпирической плотности распределения.

Эмпирической функцией распределения называется функция, вычисляемая для любого значения х по формуле:

,

где n – объем выборки,  – количество вариант, значения которых меньше, чем х.

Свойства :

      При   ;

      При   ;

      При   ;

       – функция неубывающая.

Рис. 2.4 График функции распределения

Эмпирическая плотности распределения - функция, описывающая распределение случайных значений переменной. Если переменная х принимает значения на непрерывном отрезке и имеет минимальное значение а и максимальное значение b, эмпирическая плотность распределения обозначается как f(x). Интеграл функции f(x) на отрезке от а до b:

должен быть равен 1.

9. Что называют точечной оценкой неизвестного параметра генеральной совокупности? Какую точечную оценку называют несмещенной? Какая точечная оценка является несмещенной, состоятельной и эффективной в классе линейных оценок для математического ожидания генеральной совокупности? Какая точечная оценка для дисперсии генеральной совокупности является: а) смещенной; б) несмещен­ной? Являются ли эти оценки состоятельными? В чем состоит метод максимального правдоподобия нахождения точечных оценок?

Точечной называют оценку, которая определяется одним числом. При небольших объемах выборки, чаще всего пользуются интервальными оценками.

Оценка неизвестных параметров в методе наименьших квадратов производится с помощью минимизации суммы квадратов рассогласований. Такой подход во многих важных ситуациях приводит к оценкам, обладающим важными свойствами оптимальности. 

Оценки неизвестных параметров, называемые точечными оценками, определяются одним числом. Точечной оценкой математического ожидания СВ X служит средняя арифметическая (выборочное среднее ) - обобщающая статистическая характеристика вариационного ряда. 

Оценку неизвестного параметра генеральной совокупности одним числом называют точечной оценкой. 

Для оценки неизвестных параметров применяем метод наибольшего правдоподобия. 

Несмещенность оценки. Оценка называется несмещенной, если ее математическое ожидание равно оцениваемому параметру генеральной совокупности a:

Статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых СВ.

Для того, чтобы статистические оценки давали удовлетворительные приближения оцениваемых параметров, они должны удовлетворять определённым требованиям:

1) они должны быть несмещённые;

2) эффективные;

3) состоятельные.

1. Несмещённой называют статистическую оценку О*, математического ожидание которой равно оцениваемому параметру О при любом объёме выборки М (О*)=О Смещённой называют оценку, математическое ожидание которой не равно оцениваемому параметру.

2. Эффективной называют статистическую оценку, которая имеет наименьшую возможную дисперсию при заданном объёме выборки п.

3. Состоятельной называют статистическую оценку, которая при n— стремится по вероятности к оцениваемому параметру.

Генеральное среднее - это среднее арифметическое значений признака генеральной совокупности. (Обозначается Хг)

Выборочное среднее обозначается буквой Хв, равна сумме , - математическое ожидание.

Несмещённой называют статистическую оценку О*, математического ожидание которой равно оцениваемому параметру О при любом объёме выборки М (О*)=О Смещённой называют оценку, математическое ожидание которой не равно оцениваемому параметру.

1.Состоятельность оценки. Оценка называется состоятельной, если она по вероятности с увеличением объема выборки п стремится к параметру генеральной совокупности:

Это условие будет выполняться, если

и оценка является несмещенной. Доказательство этого основано на неравенстве Чебышева.

2. Эффективность оценки. Если составлять множество несмещенных и состоятельных оценок, то эти оценки будут иметь разные дисперсии. Ясно, что, чем меньше будет дисперсия, тем меньше будет вероятность грубой ошибки при определении приближенного параметра генеральной совокупности. Поэтому нужно выбрать такую оценку, у которой дисперсия была бы минимальной:

Такая оценка называется эффективной.

Метод максимального правдоподобия

Метод максимального правдоподобия основывается на представлении выборки объема n как n-мерной случайной величине (Х1, Х2, ..., Хn), где рассматриваются как независимые случайные величины с одинаковой плотностью распределения f(x). Плотность распределения такой n-мерной случайной величины называется функцией правдоподобия L(x1, x2, ..., xn), которая в силу независимости случайных величин равна произведению плотностей распределения случайных величин Х1, Х2, ..., Хn:

L(x1, x2, ..., xn) = f(x1) f(x2)... f(xn).

Отсюда следует, что всякую функцию у=у(x1, x2, ..., xn) выборочных значений x1, x2, ..., xn,(статистику), можно представить как случайную величину, распределение которой однозначно определяется функцией правдоподобия.

Рассмотрим метод отыскания оценок параметров по опытным данным, который использует функцию правдоподобия.

Пусть f(x;а) – плотность распределения случайной величины Х (генеральной совокупности), зависящая от параметра а. Функция правдоподобия также будет зависеть от параметра а и иметь вид

Сущность метода наибольшего правдоподобия заключается в том, чтобы найти такое значение параметра а, при котором функция правдоподобия L(x1, x2, ..., xn, а) была бы максимальной. Для этого необходимо решить уравнение

и найти то значение а, при котором функция L(x1, x2, ..., xn; а) достигает максимума. С целью упрощения вычисления, так как часто плотность распределения является экспоненциальной функцией, дифференцируют натуральный логарифм функции правдоподобия, пользуясь тем, что

Если неизвестными являются несколько параметров а1, а2, ... , аm, то функция правдоподобия зависит отm параметров: L = L(x1, x2, ..., xn; а1, а2, ... , аm) и тогда решаются совместно m уравнений

Полученное решение системы относительно параметров а1, а2, ... , аm принимается в качестве оценок неизвестных параметров.

12. Что называют интервальной оценкой для неизвестного параметра распределения генеральной совокупно­сти? Что такое коэффициент доверия (доверительная вероятность), нижняя и верхняя границы интервальной оценки неизвестного параметра? Какую статистику используют для построения интервальной оценки для математического ожидания в слу­чае нормальной модели при известной дисперсии? По какому закону статистика распределена?

Интервальная оценка - это оценка, которая определяется двумя числами - концами интервала. Интервальные оценки позволяют установить точность и надежность оценки. Пусть найденная по данным выборки статистическая характеристика служит оценкой неизвестного параметра ( —> ). Будем считать постоянным числом, ясно, что точность оценки будет определяться разностью | - |. Эту разность мы будем сравнивать с дельтой ( - точность оценки) | - |< .

Надежностью (доверительной вероятностью оценки по ) называют вероятность , с которой осуществляется | - |< . Как правило, задается от 0,95 (95٪) до 0,999 (99,9 ٪).

Пусть вероятность того, что, | - |< = следовательно Р(| - |< )= . Заменим это неравенство равносильным ему: - <| - |< ; - < < + Получим Р [ - < < + ]= .

Это соотношение необходимо понимать следующим образом: вероятность того, что интервал [ - , + ] покрывает неизвестный параметр равный .

Таким образом: доверительным называют интервал [ - , + ], который покрывает неизвестный параметр, заданный надежностью .

13. Какую статистику используют для построения интервальной оценки для математического ожидания в слу­чае нормальной модели при неизвестной дисперсии? По какому закону статистика распределена? Какую статистику используют для построения интервальной оценки для дисперсии нормально распреде­ленной генеральной совокупности? По какому закону она распределена?

14. Какую статистику используют при интервальном оценивании генеральной средней в случае больших объ­емов выборки (n больше 30)? Укажите ее распределение. Какую статистику используют при интервальном оценивании генеральной доли в случае больших объемов выборки (n больше 30)? Укажите ее распределение.

15. Что такое статистическая гипотеза (гипотеза)? Какую статистическую гипотезу называют параметрической, однопараметрической, многопараметриче­ской? Какую гипотезу называют основной, альтернативной, простой, сложной?

Статистической называют гипотезу о виде неизвестного распределения, или о параметрах известных распределений. Наряду с выдвинутой гипотезой рассматривают и противоречащую ей гипотезу. Если выдвинутая гипотеза будет отвергнута, то имеет место противоречащая гипотеза. Выдвинутую гипотезу называют нулевой и обозначают Но. Конкурирующей называют гипотезу Н₁.

Нулевая гипотеза (Но) — это гипотеза о том, что есть две совокупности, которые сравниваются по одному или нескольким признакам, не отличаются. При этом предполагают, что действительное различие сравниваемых величин равно нулю, а выявленное по данным отличие от нуля несет случайный характер. Нулевая гипотеза отвергается в тех случаях, когда по выборке получается результат, который при истинности выдвинутой нулевой гипотезы маловероятен. Границей маловероятного или невозможного обычно считают а = 0,05 или 0,01; 0,001.

Параметрическая гипотеза – это гипотеза о параметрах генеральной совокупности (однопараметрической – один параметр, многопараметрической – параметров больше одного).

Непараметрическая гипотеза – это гипотеза о параметрах распределения.

Альтернативная гипотеза (Нa). При такой гипотезе исследуемый фактор оказывает существенное влияние. Это означает, что х1 не равно х2. Ефакт = |хi – х| возникает как результат влияния фактора. При существенном влиянии фактора возникает новая совокупность с новыми характеристиками.

Простая гипотеза однозначно характеризует параметр распределения случайной величины.

Сложная гипотеза состоит из конечного или бесконечного числа простых гипотез, здесь указывается некоторая область вероятных значений параметра.

16. Что такое статистический критерий? Что такое уровень значимости критерия для проверки статистических гипотез? Какое множество называют критическим для проверки статистических гипотез? В чем состоит ошибка первого рода, второго рода? Что называют мощностью критерия?

Для проверки нулевой гипотезы используют специально подобранную СВ, точное или приближённое значение которой известно. В общем случае её обозначают через U или Z-если она распределена нормально, F или v²- по закону Фишера - Снедекора.

Наблюдаемым значением критерия F называют значение критерия, вычисленное по выборкам.

Уровень значимости статистического теста — допустимая для данной задачи вероятность ошибки первого рода (ложноположительного решения, false positive), то есть вероятность отклонить нулевую гипотезу, когда на самом деле она верна.

Другая интерпретация: уровень значимости — это такое (достаточно малое) значение вероятности события p, при котором событие уже можно считать неслучайным.

Уровень значимости обычно обозначают греческой буквой  (альфа).

В стандартной методике проверки статистических гипотез уровень значимости фиксируется заранее, до того, как становится известной выборка .

Чрезмерное уменьшение уровня значимости (вероятности ошибки первого рода)  может привести к увеличению вероятности ошибки второго рода, то есть вероятности принять нулевую гипотезу, когда на самом деле она не верна (это называется ложноотрицательным решением, false negative). Вероятность ошибки второго рода  связана с мощностью критерия  простым соотношением   . Выбор уровня значимости требует компромисса между значимостью и мощностью или (что то же самое, но другими словами) между вероятностями ошибок первого и второго рода.

Обычно рекомендуется выбирать уровень значимости из априорных соображений. Однако на практике не вполне ясно, какими именно соображениями надо руководствоваться, и выбор часто сводится к назначению одного из вариантов .

После выбора определённого критерия множество всех его возможных значений разбивают на 2 непересекающихся подмножества: одно из них содержит значения критерия, при которых нулевая гипотеза отвергается, а другая - при которых она принимается.

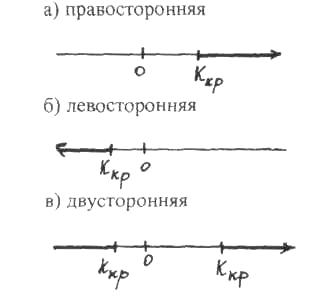
Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают.

Если наблюдаемые значения принадлежат критической области, гипотезу отвергают.

Если наблюдаемые значения критерия принадлежат области принятия гипотез -гипотезу принимаем.

Критические точки (K_кр) - точки, определяющие критическую область от области принятия гипотезы.

Правосторонней называют критическую область, определяемую неравенством К > k_кр, где k_кр - положительное число, (рис. а)

Левосторонней называют критическую область, определяемую неравенством К < k_кр, где k_кр - отрицательное число, (рис. б)

Двусторонней называют критическую область, определяемую неравенствами К < k_кр , К > k_кр, где к₂>к₁.

В итоге статистической проверки гипотезы неправильное решение может быть принято в 2-х случаях, то есть могут быть допущены ошибки 2-х родов.

Ошибка I рода состоит в том, что будет отвергнута правильная гипотеза.

Ошибка II рода состоит в том, что будет принята неправильная гипотеза.

Последствия этих ошибок могут иметь различный характер: например, если отвергнуто правильное решение «продолжать строительство жилого дома», то эта ошибка влечёт за собой материальный ущерб (риск производителя). Если же принято неправиль­ное решение «продолжать строительство», то эта ошибка может повлечь за собой гибель людей (риск потребителя).

Замечание 1. Правильное решение может быть принято также в 2-х случаях:

1. гипотеза принимается, и она действительно правильная.

2. гипотеза отвергается, и она в действительности неверна. Замечание 2.

Вероятность совершить ошибку первого рода, то есть отвергнуть правильную гипотезу, обозначают и принимают равным 0,05 или 0,01.

Вероятность ошибки первого рода при проверке статистических гипотез называют уровнем значимости и обычно обозначают греческой буквой (отсюда название -errors).

Вероятность ошибки второго рода не имеет какого-то особого общепринятого названия, на письме обозначается греческой буквой (отсюда -errors). Однако с этой величиной тесно связана другая, имеющая большое статистическое значение — мощность критерия. Она вычисляется по формуле . Таким образом, чем выше мощность, тем меньше вероятность совершить ошибку второго рода.

Обе эти характеристики обычно вычисляются с помощью так называемой функции мощности критерия. В частности, вероятность ошибки первого рода есть функция мощности, вычисленная при нулевой гипотезе. Для критериев, основанных на выборке фиксированного объема, вероятность ошибки второго рода есть единица минус функция мощности, вычисленная в предположении, что распределение наблюдений соответствует альтернативной гипотезе. Для последовательных критериев это также верно, если критерий останавливается с вероятностью единица (при данном распределении из альтернативы).

В статистических тестах обычно приходится идти на компромисс между приемлемым уровнем ошибок первого и второго рода. Зачастую для принятия решения используется пороговое значение, которое может варьироваться с целью сделать тест более строгим или, наоборот, более мягким. Этим пороговым значением является уровень значимости, которым задаются при проверке статистических гипотез. Например, в случае металлодетектора повышение чувствительности прибора приведёт к увеличению риска ошибки первого рода (ложная тревога), а понижение чувствительности — к увеличению риска ошибки второго рода (пропуск запрещённого предмета).

17. Какова схема проверки гипотезы о значении генеральной средней нормально распределенной генеральной совокупности при известной дисперсии, при неизвестной дисперсии? Какова схема проверки гипотезы о значении генеральной дисперсии нормально распределенной генераль­ной совокупности?

18. Как проверить гипотезу о равенстве дисперсий двух нормально распределенных генеральных совокупно­стей? Как проверить гипотезу о равенстве математических ожиданий двух нормально распределенных генераль­ных совокупностей?

19. Какие критерии называются критериями согласия? Как при помощи критерия ² проверить гипотезу о виде распределения непрерывной случайной величи­ны? Какая статистика используется при проверке гипотезы об однородности выборок по критерию Колмогоро­ва-Смирнова?

Решение статистических задач обычно содержит два этапа: предположение о распределении исследуемой случайной величины и изучение этой величины в рамках сделанного предположения. При этом, естественно, необходимо установить, насколько предположения о распределении случайных величин соответствуют экспериментальным данным. Принято ставить вопрос в форме: не вступает ли принятая статистическая модель в противоречие с имеющимися данными. Критерии, решающие такую задачу, называют критериями согласия.

Критериями согласия называют статистические критерии, предназначенные для обнаружения расхождений между гипотетической статистической моделью и реальными данными, которые эта модель призвана описать.

Обычно сущность проверки гипотезы о законе распределения ЭД заключается в следующем. Имеется выборка ЭД фиксированного объема, выбран или известен вид закона распределения генеральной совокупности. Необходимо оценить по этой выборке параметры закона, определить степень согласованности ЭД и выбранного закона распределения, в котором параметры заменены их оценками. Пока не будем касаться способов нахождения оценок параметров распределения, а рассмотрим только вопрос проверки согласованности распределений с использованием наиболее употребительных критериев.

Критерий хи-квадрат К. Пирсона

Использование этого критерия основано на применении такой меры (статистики) расхождения между теоретическим F(x) и эмпирическим распределением F_п(x), которая приближенно подчиняется закону распределения c ². Гипотеза Н₀ о согласованности распределений проверяется путем анализа распределения этой статистики. Применение критерия требует построения статистического ряда.

Итак, пусть выборка представлена статистическим рядом с количеством разрядов y . Наблюдаемая частота попаданий в i-й разряд n_i. В соответствии с теоретическим законом распределения ожидаемая частота попаданий в i-й разряд составляет F_i. Разность между наблюдаемой и ожидаемой частотой составит величину (n _i – F_i). Для нахождения общей степени расхождения между F(x) и F_п(x) необходимо подсчитать взвешенную сумму квадратов разностей по всем разрядам статистического ряда

. (3.7)

Величина c ² при неограниченном увеличении n имеет распределение хи-квадрат (асимптотически распределена как хи-квадрат). Это распределение зависит от числа степеней свободы k, т.е. количества независимых значений слагаемых в выражении (3.7). Число степеней свободы равно числу y минус число линейных связей, наложенных на выборку. Одна связь существует в силу того, что любая частота может быть вычислена по совокупности частот в оставшихся y – 1 разрядах. Кроме того, если параметры распределения неизвестны заранее, то имеется еще одно ограничение, обусловленное подгонкой распределения к выборке. Если по выборке определяются f параметров распределения, то число степеней свободы составит k=y – _f –1.

Область принятия гипотезы Н₀ определяется условием c ^{2£ c 2}(k;a ), где c ²(k;a ) – критическая точка распределения хи-квадрат с уровнем значимости a . Вероятность ошибки первого рода равна a , вероятность ошибки второго рода четко определить нельзя, потому что существует бесконечно большое множество различных способов несовпадения распределений. Мощность критерия зависит от количества разрядов и объема выборки. Критерий рекомендуется применять при n>200, допускается применение при n>40, именно при таких условиях критерий состоятелен (как правило, отвергает неверную нулевую гипотезу).

Для применения критерия А.Н. Колмогорова ЭД требуется представить в виде вариационного ряда (ЭД недопустимо объединять в разряды). В качестве меры расхождения между теоретической F(x) и эмпирической F_n(x) функциями распределения непрерывной случайной величины Х используется модуль максимальной разности

dn = max|F(x) - F_n(x)|. (3.8)

А.Н. Колмогоров доказал, что какова бы ни была функция распределения F(x) величины Х при неограниченном увеличении количества наблюдений n функция распределения случайной величины d_n асимптотически приближается к функции распределения . Иначе говоря, критерий А.Н. Колмогорова характеризует вероятность того, что величина d_n не будет превосходить параметр l для любой теоретической функции распределения. Уровень значимости a выбирается из условия , в силу предположения, что почти невозможно получить это равенство, когда существует соответствие между функциями F(x) и F_n(x). Критерий А.Н. Колмогорова позволяет проверить согласованность распределений по малым выборкам, он проще критерия хи-квадрат, поэтому его часто применяют на практике. Но требуется учитывать два обстоятельства.

Во-первых, в точном соответствии с условиями его применения необходимо пользоваться следующим соотношением

где .

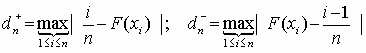Во-вторых, условия применения критерия предусматривают, что теоретическая функция распределения известна полностью (известны вид функции и ее параметры). Но на практике параметры обычно неизвестны и оцениваются по ЭД. Это приводит к завышению значения вероятности соблюдения нулевой гипотезы, т.е. повышается риск принять в качестве правдоподобной гипотезу, которая плохо согласуется с ЭД (повышается вероятность совершить ошибку второго рода). В качестве меры противодействия такому выводу следует увеличить уровень значимости a , приняв его равным 0,1 – 0,2, что приведет к уменьшению зоны допустимых отклонений.