Блочные шифры

Блочные шифры представляют собой семейство обратимых преобразований блоков (частей фиксированной длины) исходного текста.

Под N-разрядным блоком будем понимать последовательность из нулей и единиц длины N:

x = (x₀ , x₁ , …x_N-1) . (5.5)

x в Z_{2, N} можно интерпретировать как вектор и как двоичное представление целого числа

(5.6)

Под блочным шифром будем понимать элемент

Где x = (x₀ , x₁ , …x_N-1), y = (y₀ , y₁ , …y_N-1)

Хотя блочные шифры являются частным случаем подстановок, их следует рассматривать особо, поскольку, во-первых, большинство симметричных шифров, используемых в системах передачи данных, являются блочными, и, во-вторых, блочные шифры удобнее описывать в алгоритмическом виде, а не как обычные подстановки.

Потоковые шифры

Потоковые шифры представляют собой разновидность гаммирования и преобразуют открытый текст в шифрованный последовательно по одному биту. Генератор ключевой последовательности, иногда называемой генератором бегущего ключа, выдает последовательность бит k₁, k₂ , … k_N. Эта ключевая последовательность складывается по модулю 2 (“исключающее или”) с последовательностью бит исходного текста e₁, e₂ , …, e_N:

(5.7)

На приемной стороне шифрованный текст складывается по модулю 2 с идентичной ключевой последовательностью для получения исходного текста:

(5.8)

Стойкость системы целиком зависит от внутренней структуры генератора ключевой последовательности. Если генератор выдает последовательность с небольшим периодом, то стойкость системы невелика. Напротив, если генератор будет выдавать бесконечную последовательность истинно случайных бит, то получим одноразовый блокнот с идеальной стойкостью.

Потоковые шифры наиболее пригодны для шифрования непрерывных потоков данных, например, в сетях передачи данных.

Ассимметричные криптосистемы

Еще одним обширным классом криптосистем являются так называемые ассиметричные, или двухключевые криптосистемы .

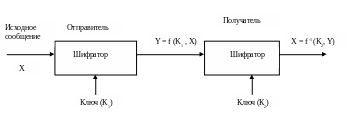
Рис. 5.2

Эти системы характеризуются тем, что для шифрования и расшифрования используются разные ключи, связанные между собой некоторой зависимостью. При этом данная зависимость такова, что установить один ключ, зная другой, с вычислительной точки очень трудно.

Один из ключей, например, ключ шифрования, можно сделать общедоступным (открытым). Тогда любой пользователь может послать зашифрованное сообщение данному абоненту, которое он расшифрует с помощью второго (секретного) ключа. Если сделать общедоступным ключ расшифрования, то на базе полученной системы можно построить систему аутентификации передаваемых сообщений, так как любой абонент, получивший послание, может проверить его подпись с помощью ключа расшифрования. Поскольку один из пары ключей общедоступен, то такие системы получили название криптосистем с открытым ключом.

Криптосистема с открытым ключом определяется темя алгоритмами: генерации ключей, шифрования и расшифрования. Алгоритм генерации ключей открыт, всякий может подать на вход генератора ключей случайную строку и получить пару ключей (k1, k2). Один из ключей публикуется, он называется открытым, а второй, называемый секретным, хранится в тайне.

Односторонние функции и функции-ловушки

Центральным понятием в теории ассиметричных криптосистем является понятие односторонней функции.

Неформально под односторонней функцией понимается эффективно вычислимая функция, для обращения которой (т.е. нахождения хотя бы одного значения аргумента по известному значению функции) не существует эффективных алгоритмов. Заметим, что обратная функция может не существовать.

Функцией-ловушкой называется односторонняя функция, для которой обратную функцию вычислить просто, если имеется некоторая дополнительная информация, и сложно, если такая информация отсутствует.

В качестве примеров задач, приводящих к односторонним функциям, можно привести следующие.

1. Разложение числа на простые сомножители. Вычислить произведение двух простых чисел очень просто. Однако для решения обратной задачи эффективного алгоритма в настоящее время не существует.

2. Дискретное логарифмирование в конечном простом поле (проблема Диффи-Хелмана). Допустим, задано большое простое число p и пусть g – примитивный элемент поля GF (p). Тогда для любого a вычислить g^a (mod p) просто, а вычислить a по заданным k = g^a (mod p) и p оказывается затруднительным.

Криптосистемы с открытым ключом основываются на одностронних функциях-ловушках. При этом открытый ключ определяет конкретную реализацию функции, а секретный ключ дает информацию о ловушке. Любой, знающий ловушку, может легко вычислять функцию в обоих направлениях, но тот, у кого такой информации нет, может производить вычисления только в одном направлении. Прямое направление используется для шифрования и верификации цифровых подписей, а обратное – для расшифровки и выработки цифровой подписи.

Во всех криптосистемах с окрытым ключом чем больше длина ключа, тем выше различия между усилиями, необходимыми для вычисления функции в прямом и обратном направлениях (для того, кто не обладает информацией о ловушке).

Пример

Пусть абоненты А и В решили наладить секретную переписку с открытым ключом. Тогда каждый из них независимо от другого выбирает два больших простых числа, находит их произведение, находит функцию Эйлера от этого произведения и выбирает случайное число, меньшее этого вычисленного значения. Функция Эйлера φ(p) равна количеству чисел, меньших p и взаимнопростых с p, т.е. не имеющих с числом p общих делителей кроме единицы; при этом если p – простое число, то φ(p) = p-1.

Итак:

A: p₁, p₂ , r_A = p_1∙ p₂ , φ(r_A), (a, φ(r_A)) = 1, 0 < a < φ(r_A)

B: q₁, q₂ , r_B = q_1∙ q₂ , φ(r_B), (b, φ(r_B)) = 1, 0 < b < φ(r_B)

Затем печатается телефонная книга, доступная всем желающим, которая имеет вид:

Абонент	А	В
Открытые ключи	rA, a	rB, b

Здесь r_A – произведение двух простых чисел p₁, p₂, известных только абоненту А; а – открытый ключ, доступный каждому, кто хочет передать сообщение А;

r_B – произведение двух простых чисел q₁, q₂, известных только абоненту B; b – открытый ключ, доступный каждому, кто хочет передать сообщение B.

Каждый из абонентов находит свой секретный ключ из сравнений:

A: α: αa ≡ 1(mod φ(r_A)), 0 < α < φ(r_A)

B: β: βb ≡ 1(mod φ(r_B)), 0 < β < φ(r_B)

Получаем следующую таблицу ключей:

Абонент	Открытые ключи	Секретные ключи
А	rA, a	α
В	rB, b	β

Пусть абонент А решает послать сообщение m абоненту В:

А: m→ B и пусть 0 < m < r_B, иначе текст делят на куски длиной r_B.

Далее абонент А шифрует свое сообщение m открытым ключом абонента В и находит

m₁ = m^b (mod r_B), 0 < m₁ < r_B

Абонент В расшифровывает это сообщение своим секретным ключом:

m₂ = m₁^β (mod r_B), 0 < m₂ < r_B

и получает m₂ = m.

Опустим формальное доказательства тождественности этих преобразований и проверим метод на конкретных числовых данных.

Пусть

p1 = 7 p2 = 23 - простые числа А

r_A = p_1∙ p₂ =161 φ(r_A) = 132

q1 = 11 q2 = 17 - простые числа В

r_B = q_1∙ pq₂ = 187 φ(r_B) = 160

a = 7 b = 9 – случайные числа, выбранные А и В соответственно.

Телефонная книга:

А: 161, 7

В: 187, 9

Каждый из абонентов находит свой секретный ключ:

А: 7∙α ≡ 1 (mod 132) → α = 19

B: 9∙β ≡ 1 (mod 160) → β = 89

Пусть абонент А решает послать абоненту В сообщение m =3.

Тогда он шифрует свое сообщение открытым ключом абонента В:

m₁ ≡ 3⁹≡ 48 (mod 187)

Абонент расшифровывает это сообщение своим секретным ключом:

m₂ ≡ 48⁸⁹≡ 3 (mod 187)

Следовательно m₂ = m =3.