4. Решение варианта 0

Задача 1. Разложение вектора X=(1,7,1) по векторам P(-1,0,2), Q(0,-2,1,) R(3,1,0) имеет вид:

X=άP+βQ+γR

Распишем это векторное уравнение покоординатно, т.е. сначала приравняем абсциссы, затем ординаты, а потом аппликаты. В результате получим систему трех линейных алгебраических уравнений с тремя неизвестными ά, β, γ::

1. Решим систему (1) методом Крамера. Для этого подсчитаем 4 определителя: главный ∆ и 3 вспомогательных ∆_ά, ∆_β, ∆_γ. Напомним, что главный определитель составляется из коэффициентов при неизвестных ά, β, γ. Вспомогательные определители формируются из главного заменой соответствующего столбца столбцом свободных членов.

Главный определитель вычислим методом Лапласа с помощью разложения, например, по первой строке:

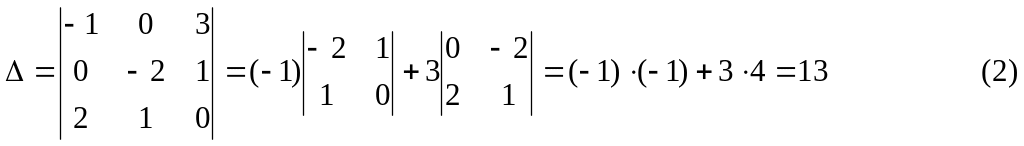
Аналогично вычисляются вспомогательные определители.

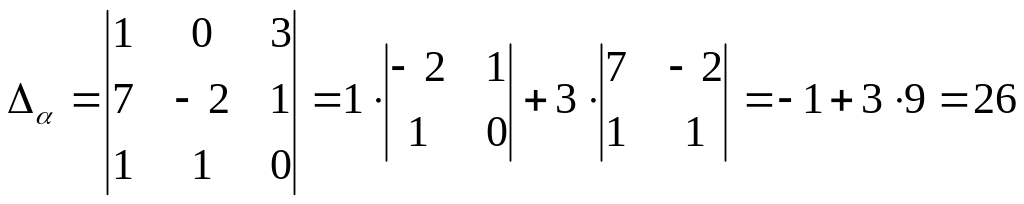
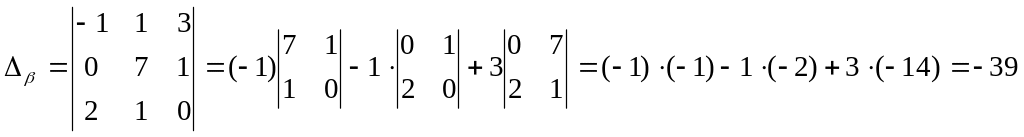
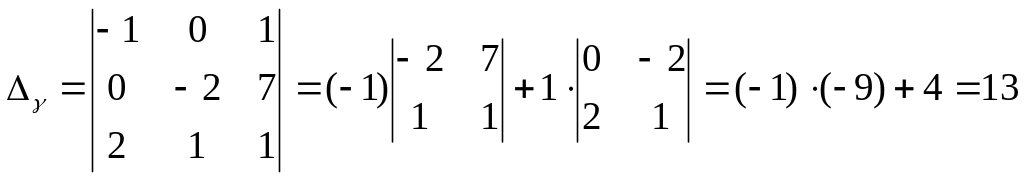
Неизвестные ά, β, γ находятся как отношения соответствующих вспомогательных определителей к главному:

2. Решим систему (1) матричным методом. Очевидно, что

X=A^-1B,

где A^-1 – обратная матрица по отношению к матрице коэффициентов системы, B – столбец свободных членов.

Найдем обратную матрицу по схеме:

A → A^* → (A^*)^T → (A^*)^T/∆=A^-1

где A – исходная матрица,

A^* - присоединенная матрица (состоящая из алгебраических дополнений каждого элемента исходной матрицы),

(A^*)^T – транспонированная матрица относительно присоединенной матрицы A^*,

∆ - определитель матрицы А

Напомним, что для нахождения присоединенной матрицы необходимо отыскать алгебраические дополнения всех элементов исходной матрицы. Алгебраическое дополнение элемента матрицы – это определитель, получающийся вычеркиванием строки и столбца, на пересечении которых находится данный элемент. Знак такого определителя меняется на противоположный, если сумма номеров строки и столбца нечетна.

Алгебраическим дополнением элемента (-1), находящегося на пересечении первой строки и первого столбца, является определитель

Алгебраическим дополнением элемента 0, находящегося на пересечении первой строки и второго столбца, является определитель

Знак определителя изменен на противоположный, так как 1+2=3 – нечетное число.

Аналогично отыскиваются алгебраические дополнения других элементов исходной матрицы.

Итак,

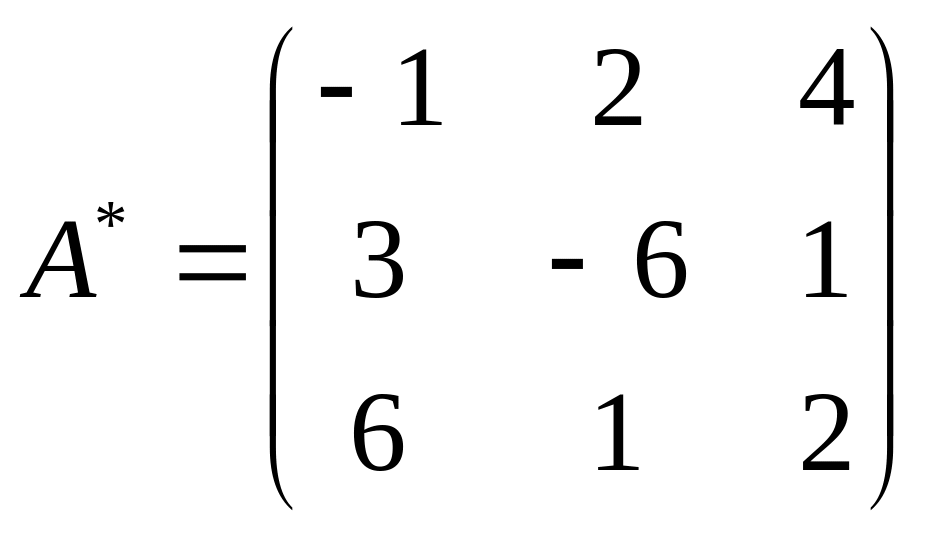
В результате транспонирования получаем

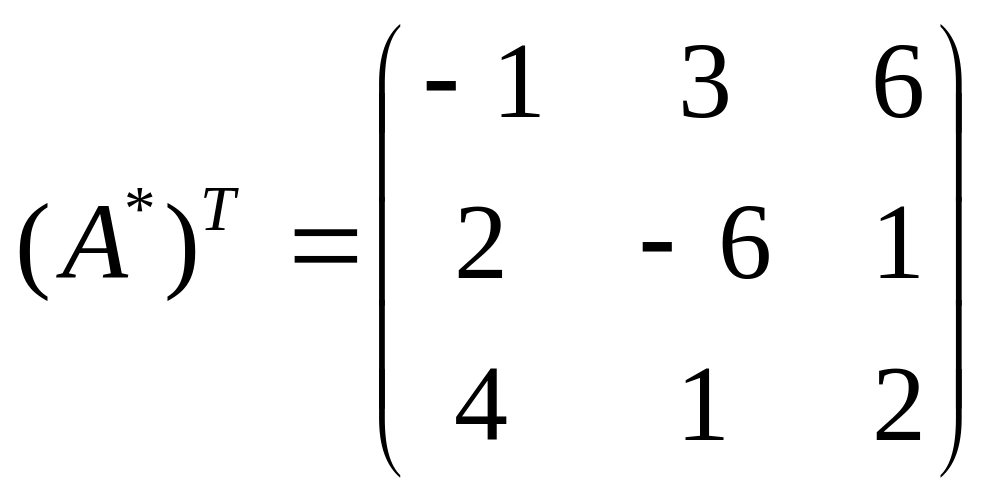
Определитель исходной матрицы был подсчитан ранее, а именно (см. формулу (2)), ∆=13. Таким образом,

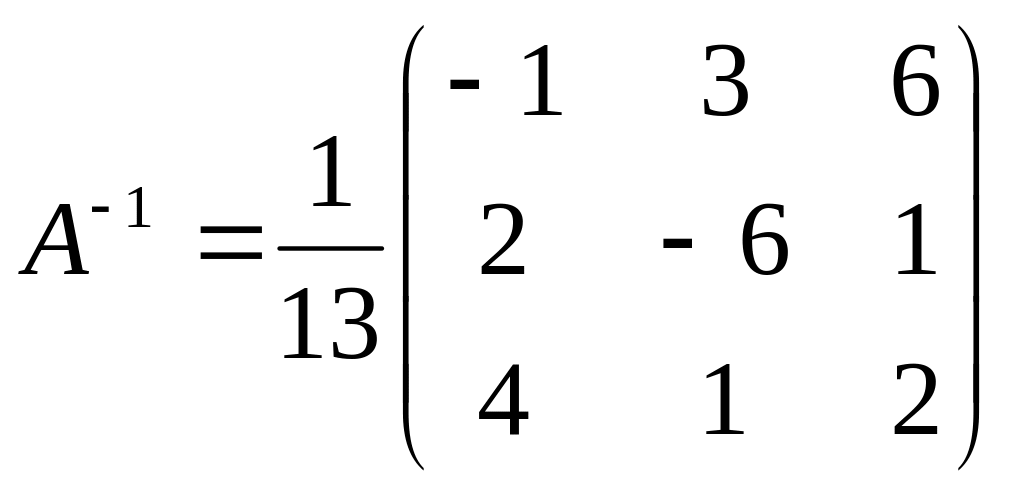
Умножая справа на столбец свободных членов, находим

или ά=2, β=-3, γ=1.

Решим систему методом Гаусса. Составим расширенную матрицу

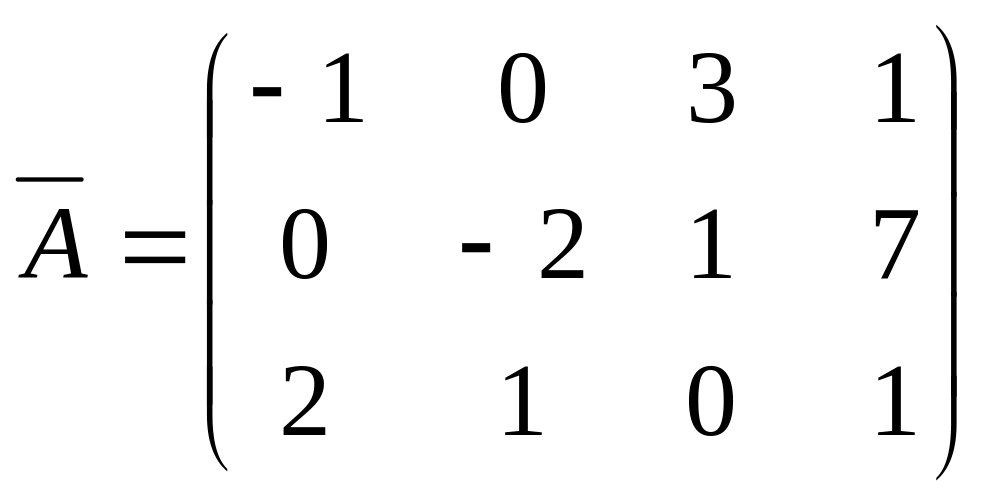
Пусть разрешающим элементом будет a₂₃=1, а разрешающей строкой – вторая строка. С помощью выбранной второй строки элементарными преобразованиями исключим переменную γ, т.е. добьемся того, чтобы все элементы третьего столбца, кроме разрешающего, оказались равными 0. А именно, если к первой строке добавить вторую, умноженную на (-3), то получим

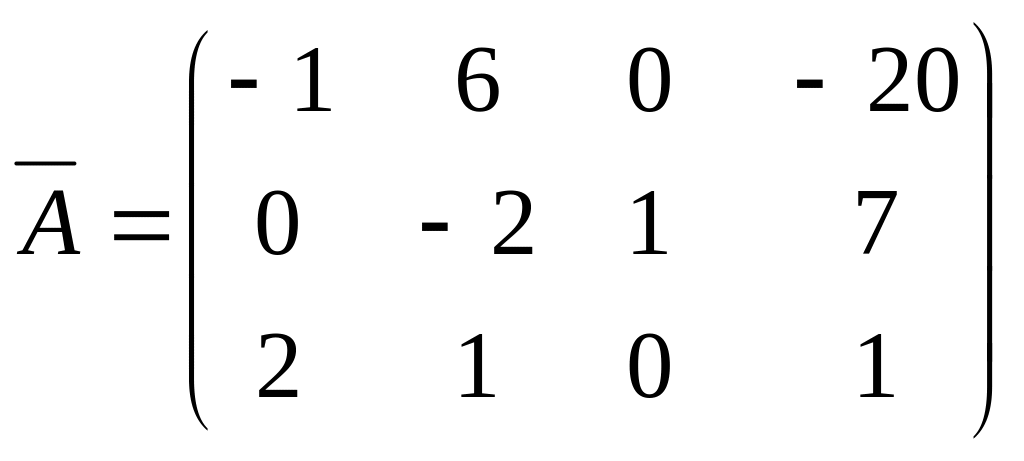
Пусть теперь разрешающим элементом будет a₃₂=1, а разрешающей строкой – третья строка. С помощью выбранной третьей строки элементарными преобразованиями исключим переменную β, т.е. добьемся того, чтобы все элементы второго столбца, кроме разрешающего, оказались равными 0. А именно, если к первой строке добавить третью, умноженную на (-6), а ко второй – третью, умноженную на 2, то получим

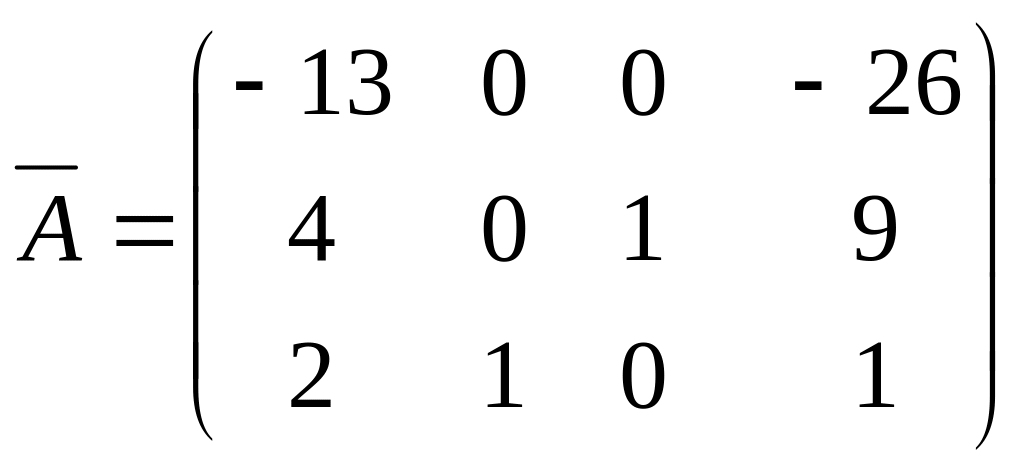
Сократим все элементы первого столбца на (-13):

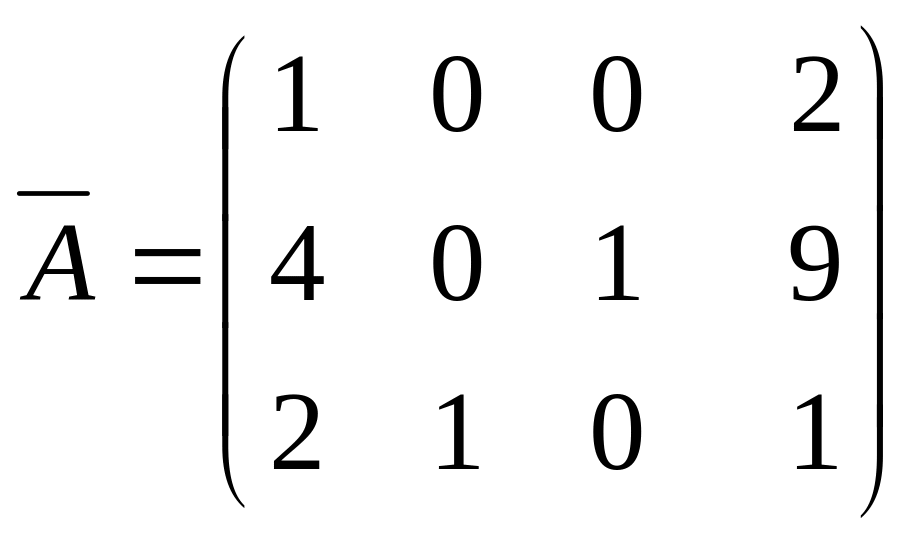
Выберем в качестве разрешающего элемент a₁₁=1. Прибавим ко второй строке первую, умноженную на (-4), а к третьей – первую, умноженную на (-2). После такого преобразования получаем

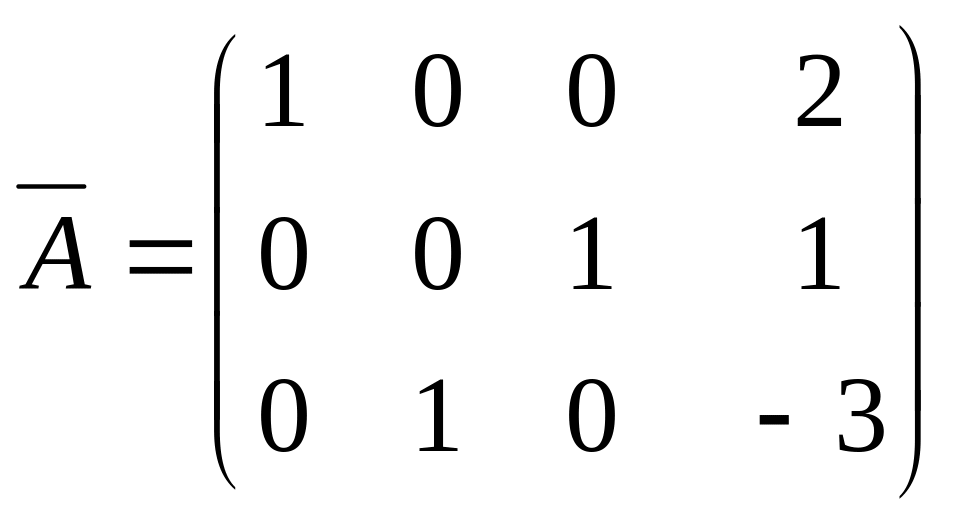
Отсюда снова получаем ά=2, β=-3, γ=1.

Итак, разложение вектора X=(1,7,1) по векторам P(-1,0,2), Q(0,-2,1,) R(3,1,0) имеет вид:

X=2P-3Q+R

Задача 2. Треугольник АВС задан своими вершинами А(2,1), B(4,-3),

C(-3,0).

1. Найдем уравнение стороны АВ, для чего воспользуемся уравнением прямой, проходящей через две точки:

Подставляя координаты точек А и В, получаем уравнение:

Итак, каноническое уравнение прямой АВ имеет вид:

Приведем это уравнение к общему виду. По правилу пропорции получаем:

-4(x-2)=2(y-1). Раскрывая скобки, приходим к общему уравнению прямой АВ:

2x+y=5

Изолируем y и получим уравнение прямой с угловым коэффициентом:

y=-2x+5

Аналогично находятся уравнения других сторон. Каноническое уравнение прямой ВС:

Общее уравнение прямой ВС:

3x+7y+9=0

Уравнение прямой ВС с угловым коэффициентом:

Каноническое уравнение прямой АС:

Общее уравнение прямой АС:

x-5y+3=0

Уравнение прямой АС с угловым коэффициентом:

2. Найдем уравнение и длину высоты AD из точки А на сторону ВС. Из канонического уравнения стороны ВС получаем направляющий вектор

q_ВС=(-7, 3)

Этот вектор можно принять в качестве нормального вектора прямой AD:

n_AD=(-7, 3)

Следовательно, уравнение прямой AD, проходящей через точку А и имеющей нормальный вектор n_AD, имеет вид:

-7(x-2)+3(y-1)=0

Раскроем скобки и приведем к общему виду:

-7x+3y+11=0

Уравнение медианы AD в явной форме имеет вид:

Далее найдем координаты точки D, для чего необходимо совместно решить уравнения прямой ВС и медианы AD:

Решим эту систему методом Гаусса (алгебраического сложения). Умножим первое уравнение на 7, а второе на 3. После сложения этих уравнений переменная x исключается, что позволяет найти y. А именно,

y=-48/29

Теперь умножим первое уравнение на -3, а второе на 7. После сложения этих уравнений переменная y исключается, что позволяет найти x. А именно,

x=25/29

Итак, D(25/29, -48/29). Длину медианы AD находим по формуле расстояния между двумя точками:

3. Для вычисления площади треугольника найдем длину стороны ВС:

Тогда площадь треугольника ABC равна

Задача 3. Тетраэдр АВСD задан своими вершинами А(2,1 4), B(-2,1,0),

C(0,-3,-5), D(1,0,-3).

1) Найдем уравнение грани ABC через смешанное произведение векторов AB, AC и AM, где М(x,y,z) – произвольная точка грани:

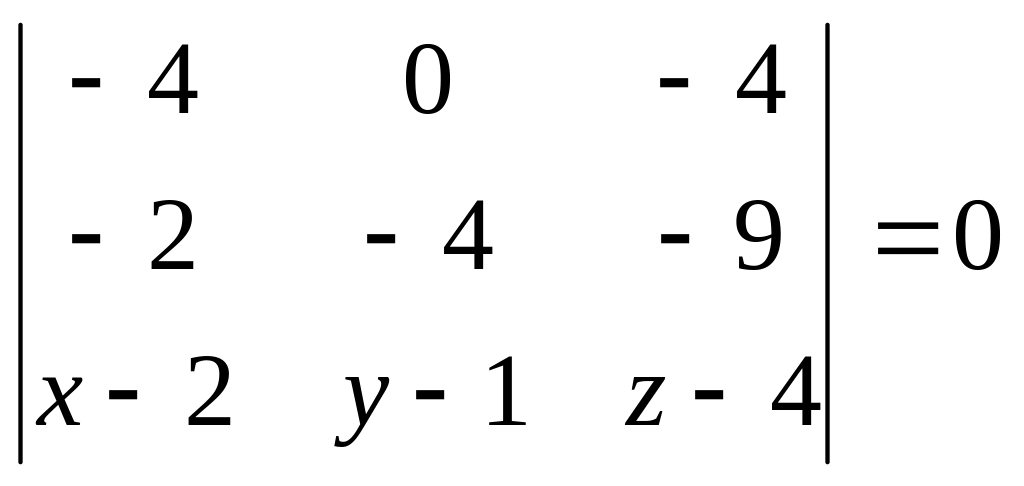
Разлагая определитель по третьей строке, получаем -16(x-2)-28(y-1)+16(z-4)=0 или

ABC: 4x+7y-4z+1=0

Аналогично находятся уравнения других граней.

2) Уравнение средней линии грани АВС будем искать в следующей последовательности: сначала вычислим координаты точек P, Q – середин сторон АВ и АС. А именно, по формулам

находим: P(0,1,2). По аналогичным формулам Q(1,-1,-0.5). Уравнение средней линии PQ запишем в канонической форме:

или

3. Объем тетраэдра вычислим по формуле

где (AB,AC,AD) – смешанное произведение этих трех векторов. Итак,

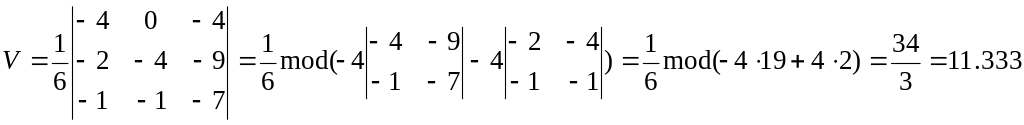
Задача 4. Найти пределы функций:

1. Сначала подставим предельную точку x=2: числитель и знаменатель дроби равны нулю. Значит, мы имеем неопределенность первого типа (0/0). По теореме Виета или через дискриминант найдем корни квадратичной формы в числителе и разложим ее на линейные множители:

x²-x-2=(x-2)(x+1)

Теперь предел можно записать так:

2. Воспользуемся таблицей эквивалентных бесконечно малых, а именно,

sin2x~2x

(Это следствие из первого замечательного предела)

Тогда

Решим эту же задачу по правилу Лопиталя. Напомним, что по этому правилу отношение дифференцируемых бесконечно малых можно заменить отношением их производных. Тогда

3. Сделаем следующие преобразования:

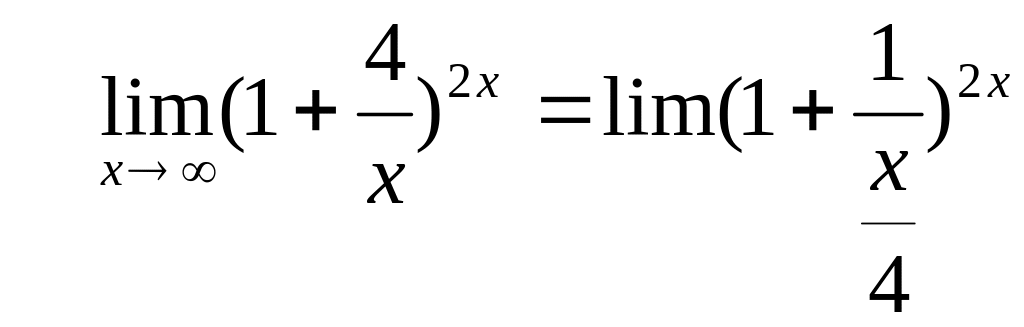
Обозначим v=x/4 и снова воспользуемся таблицей эквивалентных бесконечно малых, а именно,

(Это второй замечательный предел).

Тогда

Задача 5. Исследовать функции и построить графики

Исследование функций проведем по следующей схеме:

А) общие характеристики

• область определения

• нули

• четность

• периодичность

• особые точки

• асимптоты

В) дифференциальные характеристики

• монотонность

• экстремумы

• выпуклость

• перегибы

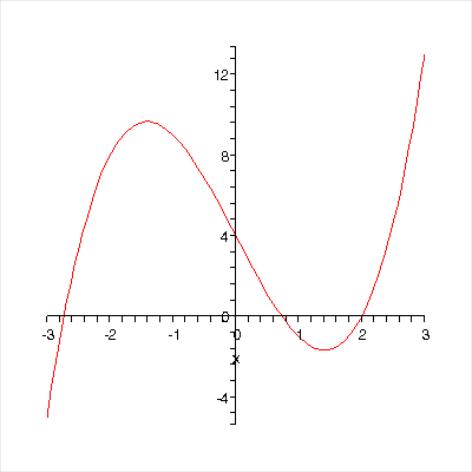
1. Рассмотрим сначала функцию

   • область определения – вся числовая прямая: D(y)=R

   • нули – точки, в которых значение функции равно нулю. Очевидно, что один корень x₁=2. Разделим (например, уголком) кубическую форму в правой части функции на линейный множитель (x-2) для отыскания еще двух других корней. Получим

x³-6x+4=(x-2)(x²+2x-2)

Квадратичная форма x²+2x-2 (по теореме Виета или через дискриминант) имеет два корня x₂=-1-√3, x₃=-1+√3. Таким образом,

D₀={-1-√3, -1+√3, 2}

• Очевидно, что это функция общего вида, т.е. не обладает свойством четности

y(x)=y(-x)

или нечетности

y(x)=-y(-x)

• Функция не является периодической, т.е. не найдется такого Т, что

y(x)=y(x+Т)

• Особые точки: y(0)=4. Значит, график функции пересекает ось ординат в точке (0,4).

• Вертикальных асимптот y=kx+b также нет, так как функция не имеет точек существенного разрыва (разрыва второго рода) хотя бы с одним односторонним бесконечным пределом. Убедимся, что нет и наклонных асимптот. Действительно,

• Исследуем функцию на монотонность. Для этого вычислим критические точки первого рода, т.е. точки, в которых производная равна нулю или не существует. Найдем производную

y^’=3x²-6

и приравняем нулю:

x²-2=0.

Критические точки: -√2, √2. Они делят область определения на три участка монотонности:

D=(-∞, -√2)U(-√2, √2)U(√2, ∞)

Исследуем направление монотонности с помощью таблицы

x	(-∞, -√2)	(-√2, √2)	(√2, ∞)
y^’	+	-	+
y	↑	↓	↑

Итак, участки монотонности:

(-∞, -√2) – участок возрастания функции

(-√2, √2) – участок убывания функции

(√2, ∞) - участок возрастания функции

• Из таблицы легко определить точки экстремума. А именно, x=-√2 – точка локального максимума функции, а x=√2 – точка локального минимума функции

• Исследуем функцию на выпуклость. Для этого вычислим критические точки второго рода, т.е. точки, в которых производная второго порядка равна нулю или не существует. Найдем производную второго порядка

y^’’=6x

Приравнивая нулю, получаем одну точку x=0. Она делит область определения функции на два участка:

D=(-∞, 0)U(0, ∞)

Исследуем направление выпуклости с помощью таблицы

x	(-∞, 0)	(0, ∞)
y^’’	-	+
y	∩	U

Итак, участки выпуклости:

(-∞, 0) – участок выпуклости вверх

(0, ∞) - участок выпуклости вниз

• Из таблицы легко определить точку перегиба. А именно, x=0 – точка перегиба функции

Используя полученную информацию, построим график заданной функции с помощью пакета Maple.

plot(x^3-6*x+4,x=-3..3);

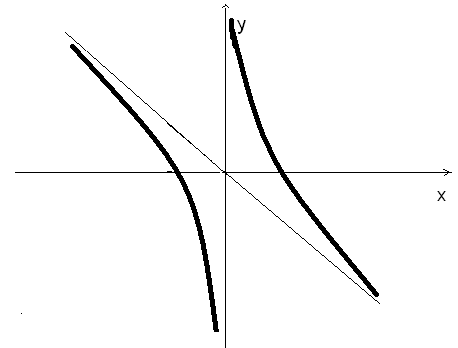
2. Рассмотрим теперь функцию

   • область определения – все точки числовой прямой, за исключением точки x=0: D(y)=R\{0}

   • нули – точки, в которых значение функции равно нулю. Приравнивая нулю числитель, получаем

D₀={-2, 2}

• Очевидно, что это нечетная функция. В самом деле,

Значит, график функции симметричен относительно начала координат.

• Функция также не является периодической, т.е. не найдется такого Т, что

y(x)=y(x+Т)

• Особые точки: x=0. Найдем односторонние пределы в этой точке:

• Полученные значения односторонних пределов позволяются сделать вывод, что функция имеет вертикальную асимптоту x=0. Убедимся, что функция имеет и наклонную асимптоту y=kx+b. Действительно,

Следовательно, y=-x+b. Найдем параметр b.

Итак, наклонная асимптота заданной функции такова: y=-x

• Исследуем функцию на монотонность. Для этого вычислим критические точки первого рода. Найдем производную

Критическая точка: 0. Она не входит в область определения функции, но является граничной для нее. Область определения в этом случае естественным образом представляется объединением двух участков монотонности:

D=(-∞,0)U(0, ∞)

Исследуем направление монотонности с помощью таблицы

x	(-∞, 0)	(0, ∞)
y^’	-	-
y	↓	↓

Итак, участки монотонности:

(-∞, 0) – участок убывания функции

(0, ∞) - участок убывания функции

• Из таблицы видно, что экстремумов функция не имеет

• Исследуем функцию на выпуклость. Для этого вычислим критические точки второго рода. Найдем производную второго порядка

Критическая тока: x=0. Она делит область определения функции на те же два участка:

D=(-∞, 0)U(0, ∞)

Исследуем направление выпуклости с помощью таблицы

x	(-∞, 0)	(0, ∞)
y^’’	-	+
y	∩	U

Итак, участки выпуклости:

(-∞, 0) – участок выпуклости вверх

(0, ∞) - участок выпуклости вниз

• Точка x=0 не является точкой перегиба, так как она не входит в область определения функции и в ней не существует производная второго порядка.

Используя полученную информацию, построим график заданной функции