43. Задачи теории игр. Классификация игр.

Различают три основных типа задач:

1. Нахождение оптимального исхода. В качестве исхода в общем случае может рассматриваться социально-экономическая ситуация. В зависимости от содержания задачи ситуацию можно описать наборами благ, получаемых каждым игроком (выигрышами), или исходом может быть избрание того или иного кандидата, принятие того или иного проекта, договора и т.д. При этом в общем случае надо найти коалиционную структуру и коалиционные стратегии, при которых оптимальный исход реализуется.

2. Нахождение оптимального исхода при фиксированной коалиционной структуре, то есть когда нам заведомо известно, что, например, образование коалиций запрещено, невозможно или имеющаяся коалиционная структура не должна меняться по каким-либо политическим или экономическим соображениям. В этом случае общей задачей является нахождение правил принятия решений в коалициях (порядок вознаграждения ее членов), при которых данная коалиционная структура не распадется, и, значит, система будет функционировать согласно интересам и возможностям ее участников.

3. Нахождение устойчивой коалиционной структуры при заданных правилах принятия решений ( конституции, нормативных актах, уставе предприятия и др.) в коалициях. Такие задачи часто встречаются при решении экономических и социальных проблем.

Игры можно классифицировать по различным признакам.

1. По количеству игроков (игры 2 и n игроков). Игра, в которой участвуют два игрока, называется парной.

2. По количеству стратегий. В зависимости от числа стратегий игры делятся на «конечные» и «бесконечные». Игра называется конечной, если у каждого игрока имеется в распоряжении только конечное число стратегий (в противном случае игра называется бесконечной). Бывают игры (например, шахматы), где в принципе число стратегий конечно, но так велико, что полный их перебор практически невозможен.

3. По характеру взаимодействия игроков. По характеру взаимодействия игроков игры делятся на:

1) бескоалиционные – игроки не имеют права вступать в соглашения, образовывать коалиции;

2) коалиционные (кооперативные) – игроки могут вступать в коалиции.

4. По характеру выигрыша. По характеру выигрыша игры можно разделить на антагонистические и игры с ненулевой суммой.

Игра называется игрой с нулевой суммой, если сумма выигрышей всех игроков в любой игровой ситуации равна нулю (т. е. каждый игрок выигрывает только за счет других).

5. По характеру получения информации. По характеру получения информации игры делятся на:

1) игры в нормальной форме – игроки получают всю предназначенную им информацию до начала игры;

2) динамические игры – информация поступает игрокам в процессе развития игры.

44. Матричные игры. Решение матричной игры в чистых стратегиях. Смешанные стратегии.

Парная, конечная, антагонистическая игра называется матричной.

Рассмотрим такую игру G(X,Y,K), в которой участвуют два игрока, имеющие противоположные интересы: выигрыш одного равен проигрышу другого. Так как выигрыш первого игрока равен выигрышу второго игрока с обратным знаком, мы можем интересоваться только выигрышем а первого игрока. Естественно, первый игрок хочет максимизировать, а второй — минимизировать а.

X и Y -- непустые множества стратегий для 1 и 2 игроков соответственно, элементы декартова произведения X×Y (т.е. пары стратегий (x,y), где x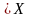 , y --ситуации), а функция К: X×Y→R называется функцией выигрыша первого игрока.

Пусть у первого игрока имеется m стратегий, а у второго игрока n стратегий. Допустим, что из своих m стратегий первый игрок выбирает i-ю (i=1,…,m), а второй игрок j-ю (j=1,…,n). Тогда определяется выигрыш первого игрока, равный . Если выигрыш равен отрицательному числу, то речь идет о фактическом проигрыше игрока. Матрица А называется платежнойматрицей, или матрицей выигрыша:

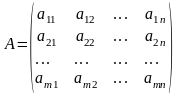
Решение матричной игры в чистых стратегиях.

Главным в исследовании игр является понятие оптимальных стратегий игроков. В это понятие интуитивно вкладывается такой смысл: стратегия игрока является оптимальной, если применение этой стратегии обеспечивает ему наибольший гарантированный выигрыш при всевозможных стратегиях другого игрока.

Исходя из этих позиций, игрок 1 исследует матрицу выигрышей А следующим образом:

для каждого значения i (i=1,2,..,m) определяется минимальное значение выигрыша в зависимости от применяемых 2-м игроком стратегий j(i=1,2,...n): .

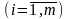Т.е. определяется минимальный выигрыш для игрока 1 при условии, что он примет свою i-ю чистую стратегию, а затем из этих минимальных выигрышей отыскивается такая стратегия i = i₀, при которой этот минимальный выигрыш будет максимальным, т.е. находится , .

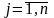Число 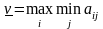называется нижней ценой игры и показывает, какой наибольший гарантированный выигрыш может обеспечить себе игрок 1, применяя свои чистые стратегии при всевозможных действиях игрока 2.

Принцип оптимальности в поведении 1-го игрока, который заключается в достижении им наибольшего гарантированного выигрыша, называется принципом максимина, т.е. – это максимин. Оптимальная стратегия 1-го игрока, при которой достигается , называется максиминной.

Игрок 2 при оптимальном своём поведении должен стремиться по возможности за счёт своих стратегий максимально уменьшить выигрыш игрока 1:

Поэтому для игрока 2 отыскивается , т.е. определяется максимальный проигрыш игрока 1, при условии, что игрок 2 применит свою j-ю стратегию. При этом наименьший из возможных проигрышей составит , .

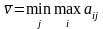Число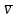 называется верхней иеной игры. Принцип оптимальности в поведении 2-го игрока, который заключается в достижении им наименьшего из возможного проигрыша, называется принципом минимакса, т.е. – это минимакс. Оптимальная стратегия 2-го игрока, при которой достигается , называется минимаксной.

Теорема:

Нижняя цена игры не превосходит верхней цены игры.

Доказательство.

и , .

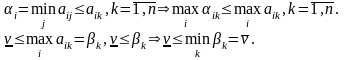
Т.о., теорема доказана.

Оптимальной ситуацией в игре G = (X, Y, К) называют пару стратегий (x*, y*), от которой ни одному из игроков невыгодно отклоняться.

Такая ситуация (x*, y*) называется равновесной, а принцип оптимальности, основанный на построении равновесной ситуации, – принципом равновесия.

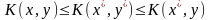
В антагонистической игре G = (Х, Y, К) ситуация (x*, y*) называется ситуацией равновесия или седловой точкой, если . Число называется значением игры.

Если в игре с матрицей A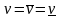 , то говорят, что эта игра имеет решение в чистых стратегиях и точка матрицы выигрыша (i₀, j₀), для которой выполняется условие для всех , , называется седловой точкой.

В седловой точке элемент матрицы 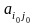является одновременно минимумом в своей строке и максимумом в своем столбце.

Теорема:

Матричная игра G(X, Y, K) имеет решение (x*, y*, v) в чистых стратегиях 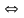игровая ситуация (x*, y* ) является равновесной.

Игры, в которых достигается ситуация равновесия, называются вполне определенными.

Решение игры в смешанных стратегиях.

Исследование в матричных играх начинается с нахождения её седловой точки в чистых стратегиях. Если матричная игра имеет седловую точку в чистых стратегиях, то нахождением этой седловой точки заканчивается исследование игры. Если же в игре нет седловой точки в чистых стратегиях, то можно найти нижнюю и верхнюю чистые цены этой игры, которые указывают, что игрок 1 не должен надеяться на выигрыш больший, чем верхняя цена игры, и может быть уверен в получении выигрыша не меньше нижней цены игры. Улучшение решений матричных игр следует искать в использовании секретности применения чистых стратегий и возможности многократного повторения игр в виде партии. Этот результат достигается путём применения чистых стратегий случайно, с определённой вероятностью.

Смешанной стратегией игрока называется полный набор вероятностей применения его чистых стратегий.

Пусть имеется матричная игра G(X, Y, K). Если игрок 1 имеет m чистых стратегий 1,2,... m, то вектор х = (p₁, p₂,..., p_m), где 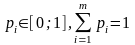, i=1,2,…,m есть смешанная стратегия первого игрока.

Аналогично для игрока 2, который имеет n чистых стратегий, смешанная стратегия у – это вектор y = (q₁, q₂,..., q_n), где , i=1,2,…,n.

Чистая стратегия есть частный случай смешанной стратегии. Действительно, если в смешанной стратегии какая-либо i-я чистая стратегия применяется с вероятностью 1, то все остальные чистые стратегии не применяются. И эта i-я чистая стратегия является частным случаем смешанной стратегии.

Оптимальная стратегия игрока – это стратегия, обеспечивающая ему максимально возможный гарантированный средний выигрыш при достаточно большом повторении ходов игры.

Средний выигрыш игрокаK(X, Y) 1 в матричной игре с матрицей А выражается в виде математического ожидания его выигрышей

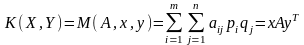
Первый игрок имеет целью за счёт изменения своих смешанных стратегий х максимально увеличить свой средний выигрыш K(X, Y) = M(А, х, у), а второй – за счёт своих смешанных стратегий стремится сделать M(А, х, у) минимальным, т.е. для решения игры необходимо найти такие х и у, при которых достигается верхняя цена игры 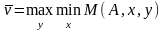, а нижняя цена игры должна быть равна

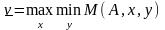
Подобно играм, имеющим седловые точки в чистых стратегиях, вводится следующее определение: оптимальными смешанными стратегиями игроков 1 и 2 называются такие наборы (х*, у*) соответственно, которые удовлетворяют равенству .

Величина v=M(А, х*, у*) называется при этом ценой игры.

Имеется и другое определение оптимальных смешанных стратегий: (х*, у*) называются оптимальными смешанными стратегиями соответственно игроков 1 и 2, если они образуют седловую точку:

M(А, х, y*)  M(А, х*, y*)  M(А, х*, у)

Оптимальные смешанные стратегии и цена игры (х* ,у*, v) называются решением матричной игры.

Теорема:

Всякая матричная игра имеет ситуацию равновесия (седловую точку) в смешанных стратегиях.