
- •Отношение эквивалентности
- •Свойства бинарных отношений
- •Метод Гаусса . Решение систем линейных уравнений.
- •Метод Крамера. Определитель второго и третьего порядков.
- •Элементы комбинаторики.
- •Свойства числа сочетаний
- •Определитель n-го порядка.
- •Разложение определителя по строке (столбцу).
- •Правило Крамера
- •Следствия из теоремы.
- •Решение матричных уравнений
- •Комплексные числа
- •Алгебраические операции над комплексными числами.
- •Линейные пространства
- •Линейная зависимость векторов .
- •Базис. Размерность.
- •Ранг матрицы
- •Матрица перехода
- •Система линейных уравнений
- •Теорема Кронекера - Капели
- •Система линейных однородных уравнений
- •Система однородных уравнений.
- •Линейные преобразования
- •Евклидово пространство
- •Свойства скалярного произведения
- •Процесс ортоганизации.
- •Векторная алгебра.
- •Скалярное произведение векторов в ортогональном базисе.
- •Двойное векторное произведение
- •Уравнение прямой и плоскости
- •Уравнение плоскости
- •Некоторые задачи о прямых и плоскостях.
- •Уравнение плоскости, проходящее через три заданных числа.
- •Расстояние от точки a до плоскости.
- •Расстояние от точки до прямой.
- •Расстояние между непараллельными прямыми в пространстве.
- •Кривые второго порядка
- •Уравнение касательной к эллипсу
- •Гипербола
- •Парабола
- •Поверхность второго порядка
- •Поверхности вращения
- •Эллипсоид
- •Конус второго порядка
- •Однополостный гиперболоид
- •Двуполостный гиперболоид
- •Эллиптический параболоид
- •Гиперболический параболоид
- •Математический анализ
- •Абсолютная величина u ее свойства
- •Последовательности.
- •Основные свойства бесконечно малых последовательностей.
- •Сходящиеся последовательности .
- •Монотонные последовательности.
- •Число е
- •Функция
- •Предел функции.
- •Непрерывные функции.
- •Классификация точек разрыва функции Точка устранимого разрыва.
- •Разрыв первого рода (конечный скачок)
- •Разрыв второго рода.
Система линейных уравнений
Рассмотрим систему уравнений общего вида
 (1) её можно переписать в виде
(1) её можно переписать в виде
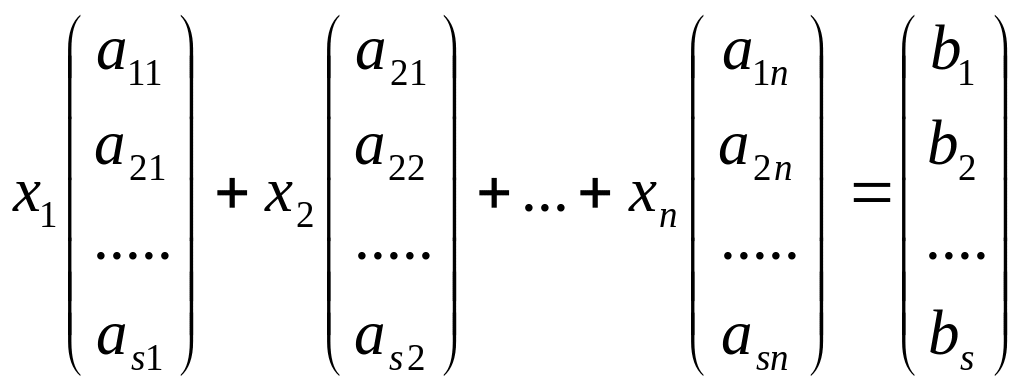
Решение системы (1) сводится к задаче о
разложении столбца свободных членов
по столбцам
![]() .
Для этого необходимо и достаточно, чтобы
столбцы расширенной матрицы и столбцы
матрицы коэффициентов имели одинаковые
ранги.
.
Для этого необходимо и достаточно, чтобы
столбцы расширенной матрицы и столбцы
матрицы коэффициентов имели одинаковые
ранги.
 (2)
(2)
 (3)
(3)
rang
![]() = rang
= rang
![]() (4)
(4)
Теорема Кронекера - Капели
Критерии совместности системы линейных уравнений.
Для совместной системы
(1) необходимо и достаточно чтобы rang
= rang
![]() (расширенной) (соотношение (4)).
(расширенной) (соотношение (4)).
С помощью теоремы Кронекера – Капели можно реализовать другой подход к решению систем линейных уравнений.
Пример. Решить систему уравнений.
![]()
Выпишем матричные коэффициенты А

Найдем ранг матрицы А по формулам окаймляющих миноров.
![]() - корневой
определитель.
- корневой
определитель.


rang A = 2
Вычислим rang расширенной матрицы А.
 rang
= 2
rang
= 2
![]()
![]()
![]()
![]()
Общее решение представлено в виде


Система линейных однородных уравнений
Система линейных однородных уравнений
![]() (5)
(5)
Система однородных
уравнений всегда совместна , так как
она с одной стороны обладает нулевым
решением с другой стороны нулевой
столбец не может изменить ранга матрицы
коэффициентов . Заметим для того, чтобы
однородная система уравнений обладала
не нулевым решением, нужно потребовать,
чтобы ранг матрицы коэффициентов был
меньше числа неизвестных
![]() .
.
Множество решений системы однородных уравнений обладает любопытными свойствами .
Свойства:
1)Если
вектор
![]() является решением системы однородных
уравнений , то вектор
является решением системы однородных
уравнений , то вектор
![]() также является решением системы
однородных уравнений.
также является решением системы
однородных уравнений.
Доказательство : i – тое уравнение системы (5) можно представить в виде
![]()
Пусть
вектор
с координатами
![]() ,
является решением системы(5) тогда
,
является решением системы(5) тогда
![]() .Подставим
координаты
.Подставим
координаты
![]() в левую часть i
– того уравнения получим
в левую часть i
– того уравнения получим
![]()
Так как вектор является решением системы (5) , получим что выражение было искомое . В силу произвольности выбора i –того уравнения свойство 1 доказано.
2) Если
вектора
и
![]() являются решением системы (5) , то их
линейная комбинация также является
решением системы (5) .
являются решением системы (5) , то их
линейная комбинация также является
решением системы (5) .
Доказательство
: Пусть
вектор
и
![]() является решением системы (5)
.Составим линейную комбинацию векторов
и
.
является решением системы (5)
.Составим линейную комбинацию векторов
и
.
![]()
Подставим координаты линейной комбинации в i-тое уравнение системы (5).Получим
![]()
В силу дистрибутивности следует
![]()
Так как вектора
![]() является решением системы (5)получим .
является решением системы (5)получим .
В силу произвольности выбора i –того уравнения свойство 2 доказано.
Доказанные свойства позволяют говорить о множестве решений систем линейных однородных уравнений как о линейном пространстве .
Система однородных уравнений.
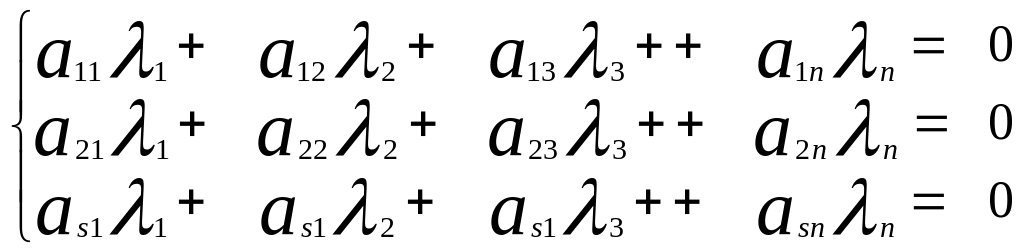 (1)
(1)
Множество решений системы (1) является линейным пространством , ранее линейное пространство определяемое базисом , порождающим линейное пространство.
Определение: Базис пространства решений системы (1) называется фундаментальной системой решения.
Теорема: Если ранг r матрицы коэффициентов r<n, то система обладает фундаментальной системой решений.
Доказательство: Пусть для определенности базисный минор порядка r, расположенного в верхнем левом углу, тогда систему(1) можно переписать в эквивалентном виде:
 (2)
(2)
Корневой определитель
системы (2)
![]() .
Общее решение системы может быть получено
по методу Крамера в зависимости от n-r
параметров. Найдем n-r
частных решений системы (2), таким образом,
что бы значения свободных параметров
образовывали единичную матрицу порядка
n-r.
.
Общее решение системы может быть получено
по методу Крамера в зависимости от n-r
параметров. Найдем n-r
частных решений системы (2), таким образом,
что бы значения свободных параметров
образовывали единичную матрицу порядка
n-r.

Построенная система векторов, линейно независима, т.к. составлена из координат векторов матрицы
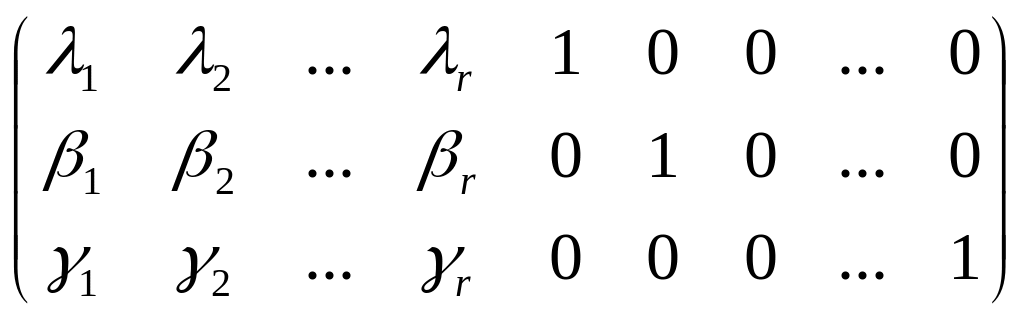
Замечаем в этой матрице
минор порядка
![]()
Для доказательства теоремы остается доказать, что любое решение системы(1) является линейной комбинацией выписанных векторов.
Возьмем произвольный
вектор
![]() ,
являющийся решением системы(1), рассмотрим
вектор
,
являющийся решением системы(1), рассмотрим
вектор![]() ,
,
![]()
![]()
Согласно свойствам
решений, однородных
линейных
уравнений, вектор
![]() также является решением системы(1).
также является решением системы(1).
Заметим, что в координатной форме можно представить в виде:
![]()
Являясь решением системы, , должен удовлетворять соотношением (2), причем свободные параметры равны 0.
Решая систему (2) при
нулевых параметрах, получим что
![]()
т.е.
является нулевым и произвольное решение
системы(1) можно представить в виде:
![]() ,
т.е. построена система векторов является
фундаментальной системой решений для
системы(1).
,
т.е. построена система векторов является
фундаментальной системой решений для
системы(1).
2.28 Пример:

Найдем общее решение по методу Гаусса.



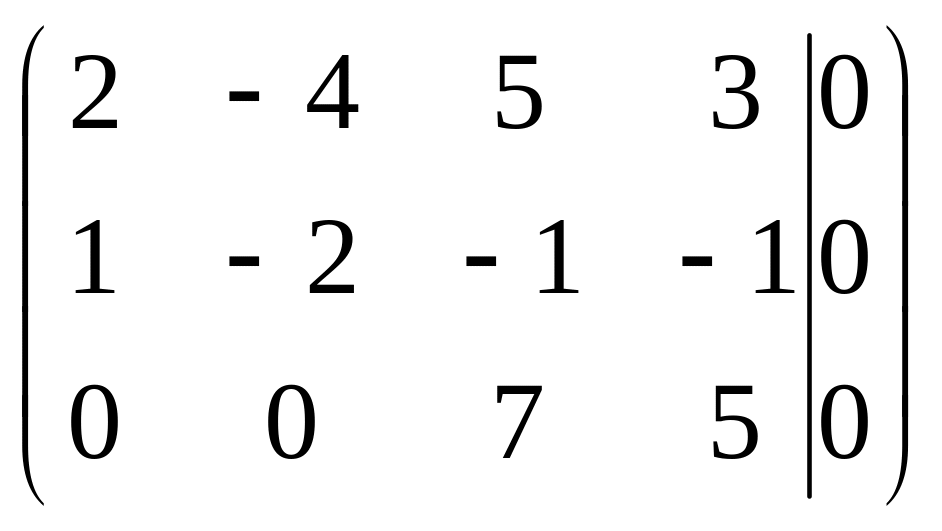



RangA=2
![]()
![]()
![]()
![]()

 общее решение
общее решение
Для построения фундаментальной системы общего решения, рисуют вспомогательную таблицу.
v v
|
|
|
|
|
|
2 |
1 |
0 |
0 |
|
|
0 |
|
1 |
Решение можно представить
в векторном виде,
![]() -
произвольные величины.
-
произвольные величины.
![]()
Для построения фундаментальной системы решений, не обязательно использовать единичную матрицу, необходимо записать матрицу порядка n-r, которая отлична от нуля.
В некоторых случаях приходится решать обратную задачу, при заданном базисе найти систему уравнений, решение которой совпадает с линейным пространством, натянутый на этот базис.
Пример: пусть базис
состоит из векторов
![]() и
и
![]() .
.
Рассмотрим произвольный
вектор
![]() ,
вектор
,
вектор
![]() является линейной комбинацией векторов
является линейной комбинацией векторов
![]() .
.
![]() .
Это означает, что вектора
,
.
Это означает, что вектора
,
![]() линейно зависимы, то есть ранг матрицы
коэффициентов составленных из этих
векторов не может равняться 3.
линейно зависимы, то есть ранг матрицы
коэффициентов составленных из этих
векторов не может равняться 3.
Составим из коэффициентов векторов матрицу:
Разложение будет иметь
место, когда ранг матрицы, составленный
из векторов
![]() .
Элементарными преобразованиями строк
записанной матрицы, решим вопрос о
рангах матрицы векторов
,
и ранге расширенной матрицы
.
Элементарными преобразованиями строк
записанной матрицы, решим вопрос о
рангах матрицы векторов
,
и ранге расширенной матрицы

![]()











 ~
~
![]() ~
~
![]() ~
~
~









![]() ~
~![]() ~
~
~![]()
ранг расширенной матрицы=2
Таким образом, получили систему уравнений.
![]()
Линейные неоднородные уравнения
 (3)
(3)
Наряду с системой (3) рассмотрим соответственную систему однородных уравнений
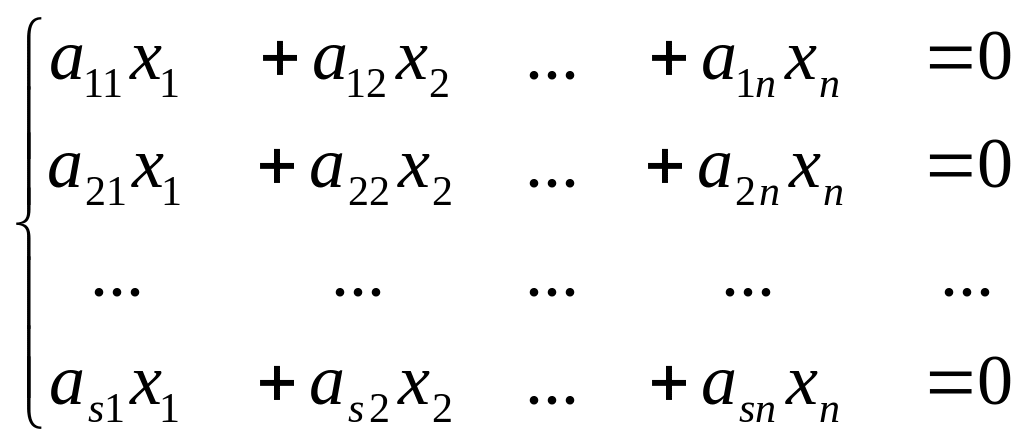 (4)
(4)
Система (4) называется приведенной системой неоднородного уравнения (3), непосредственно проверкой устанавливаются следующие свойства в системы (3)
10
Пусть
![]() произвольные решения системы (3), тогда
произвольные решения системы (3), тогда
![]() являются
произвольным решением системы (4).
являются
произвольным решением системы (4).
20
Если
![]() некоторое
решение системы (3), то общее решение
системы (3) имеет вид
некоторое
решение системы (3), то общее решение
системы (3) имеет вид
![]() ,
где
,
где
![]() -фундаментальная
система решения приведенной системы
решений (3) в векторном виде.
-фундаментальная
система решения приведенной системы
решений (3) в векторном виде.
Таким образом, общее решение системы (3) представлена в векторном виде.
![]() (5)
(5)
В соотношение (5)
-
частное решение системы (3);
соотношение (5)
-
частное решение системы (3);
![]() -
вектора фундаментальной системы решений
(3).
-
вектора фундаментальной системы решений
(3).
Частным случаем представления (5) является векторное, параметрическое уравнение прямой.
![]()
Определение: Множество решений системы (3) называются линейным многообразием.
Из выражения (3) следует, что линейное многообразие получается из линейного пространства сдвигом на некоторой вектор частного решения.
Пример: решите систему неоднородных уравнений в векторном виде.








![]()

Пусть параметры нулевые.

|
|
|
|
|
|
|
0 |
1 |
1 |
0 |
0 |
|
0 |
1 |
0 |
1 |
0 |
|
1 |
-5 |
0 |
0 |
3 |
Общее решение можно представить в виде:

