Лабораторная работа № 2

Федеральное агентство по образованию РФ

Санкт-Петербургский государственный электротехнический университет

Кафедра МО ЭВМ

Минимизация логических функций методом Квайна-МакКласки.

Преподаватель: Красюк В.И.

Студент гр. 4351 Кузьменко А.

Санкт-Петербург

2007

Часть 2. Минимизация логических функций методом Квайна-МакКласки.

В части 1 было рассмотрено представление логических функций в виде формул и введено понятие минимальных нормальных форм. Неформально можно определить минимальную форму как формулу, содержащую не большее число символов, чем любая другая формула для рассматриваемой функции.

Для формального определения введем понятие импликант и конституэнт. При этом в их качестве будем рассматривать только простые конъюнкции, то есть конъюнкции входных параметров или их отрицаний (например).

Конституэнта единицы – это функция, принимающая значение 1 только на одном наборе входных данных. Таким образом, СДНФ – это дизъюнкция конституэнт единицы, на которых функция принимает единичные значения. Пусть х – конституэнта единицы. Тогда модуль |x| - это десятичное представление двоичного числа, соответствующего x (младший разряд – слева), а индекс ind(x) – это количество единиц в наборе параметров, при котором x=1. Например, для конституэнты единицы , |x|=12, ind(x)=2.

Импликанта функции f – это функция g, имеющая единичные значения только на тех наборах входных параметров, на которых значение функции f тоже 1. Если Т_f – множество наборов входных параметров, при которых функция равна 1, то g – импликанта f по единицам, если Т_g  Т_f .

Собственная часть элементарной конъюнкции f – это конъюнкция части параметров, входящих в f, при чем отрицания сохраняются. Например, собственные части : .

Импликанта g – простая импликанта функции f, если никакие сообственные части g не являются импликантами f. Система простых импликант не избыточна, если ее импликанты покрывают все конституэнты единицы функции (импликанта g покрывает конституэнту x, если Т_x  Т_g) и при удалении любой импликанты это условии нарушается (появляются непокрытые конституэнты).

Теперь можно дать формальное определение МДНФ: минимальная форма функции – это неизбыточная дизъюнкция ее простых импликант.

Таким образом, задача минимизации любой функции сводится к нахождению простых импликант для этой функции и удалению из этого множества избыточных импликант.

Для решения этой задачи введем операции склеивания и поглощения. Пусть a и b – простые конъюнкции, тогда верны следующие утверждения:

- поглощение,

- склеивание.

С помощью операции склеивания можно построить простые импликанты функции, а с помощью операции поглощения – удалить избыточные.

При выполнении этих действий будем опираться на следующие теоремы:

1. Теорема МакКласки. Необходимым и достаточным условием склеивания двух конституэнт единицы x_l и x_k является:

   1. |ind(x_l) - ind(x_k)|=1;

   2. | |x_l| - |x_k| | = 2^m, где m – целое;

   3. |x_l| > |x_k| => ind(x_l) > ind(x_k).

Две склеенные конституэнты единицы будем называть импликантами второго уровня, две склеенные импликанты второго уровня – импликантами третьего уровня и т.д.

Импликанты второго уровня будем обозначать парой конституэнт единицы (x_l, x_k) , представленных их модулями и числом ₁=| |x_l| - |x_k| |. Так, например при склеивании конституэнт импликанту второго уровня обозначим (2, 6) - (4). Импликанту 3-го уровня будем обозначать четверкой чисел – объединением пар, соответствующих склеенным импликантам 2-го уровня, а также парой (₁, ₂), где ₂==| |x_l| - |x_k| |, x_l, x_k – первые элементы пар импликант 2-го уровня. Например, при склеивании пары (0, 2) - (2) и (8, 10) - (2) получим (0, 2, 8, 10) - (2, 8). Аналогично производится склеивание импликант более высокого уровня.

2. Для склеивания двух импликант n-го уровня (n>1) необходимо и достаточно, чтобы у них:

   1. совпадали последовательности (1, 2 ,…, n-1)

   2. младшие конституэнты единицы в обозначении импликант склеивались по первой теореме.

Для минимизации функции f необходимо производить склеивание импликант, пока оно возможно. Для этого разбивают конституэнты на группы по индексам, склеивать можно только конституэнты из разных групп. Затем строят таблицу, выделяя эти группы и уровни импликант и заполняют ее.

При этом если новый импликант совпадает с полученным ранее, он не фиксируется. В ходе склеиваний отмечаются простые импликанты, не участвовавшие в склеивании импликант более высокого уровня. Таким образом, получим систему простых импликант.

Для удаления избыточных импликант просмотрим список простых импликант, начиная с самого высокого уровня. Будем вычеркивать импликанту, если все конституэнты, входящие в нее были покрыты ранее. Затем из оставшихся выберем импликанты, включающие наибольшее количество непокрытых конституэнт и включим в систему, удалив вновь образовавшиеся избыточные ее элементы, продолжив таким образом, составим неизбыточную систему простых импликант.

Затем надо перейти от принятых обозначений импликанты к формуле. Для этого сначала надо просмотреть список (₁, ₂ ,…, _n-1). В импликанту не входят параметры с индексами (log₂_i)+1. Остальные параметры или их отрицания входят. Можно выбрать любую конституэнту и, построив ее формулу, расставить отрицания для параметров полученной импликанты. Например, восстановим формулу для импликанты (0, 8, 16, 24) - (8, 16). Так как (log₂8)+1=4, (log₂16)+1=5, а 0=00000, то искомая формула - .

Восстановив таким образом формулы простых импликант, составим их дизъюнкцию и получим минимальную форму логической функции.

Минимизируем описанным методом функцию T = {0, 4, 8, 10, 11, 12, 14, 15, 16, 17, 18, 19, 20, 24, 25, 26, 27, 28}. Выделены простые импликанты.

гр	1	ур-нь 2			уровень 3			уровень 4
0	0	0, 4 0, 8 0, 16		4 8 16	0, 4, 8, 12 0, 4, 16, 20 0, 8, 16, 24		4, 8 4, 16 8, 16	0, 4, 8, 12, 16, 20, 24, 28		4, 8, 16
1	4 8 16	8, 10 8, 12 16, 17 16, 18 16, 20 16, 24		2 4 1 2 4 8	8, 10, 12, 14 8, 10, 24, 26 8, 12, 24, 28 16, 17, 18, 19 16, 17, 24, 25 16, 18, 24, 26 16, 20, 24, 28		2, 4 2, 16 4, 16 1, 2 1, 8 2, 8 4, 8	16, 17, 18, 19, 24, 25, 26, 27		1, 2, 8
2	10 12 17 18 20 24	10, 11 10, 14 12, 14 17, 19 18, 19 17, 25 24, 25 10, 26 18, 26 24, 26 12, 28 20, 28 24, 28		1 4 2 2 1 8 1 16 8 2 16 8 4	10, 11, 14, 15 10, 11, 26, 27 17, 19, 25, 27 18, 19, 26, 27 24, 25, 26, 27		1, 4 1, 16 2, 8 1, 8 1, 2
3	11 14 19 25 26 28	11, 15 14, 15 11, 27 19, 27 25, 27 26, 27		4 1 16 8 2 1
4	15 27

Неизбыточная система простых импликант:

(0, 4, 8, 12, 16, 20, 24, 28) – (4, 8, 16)
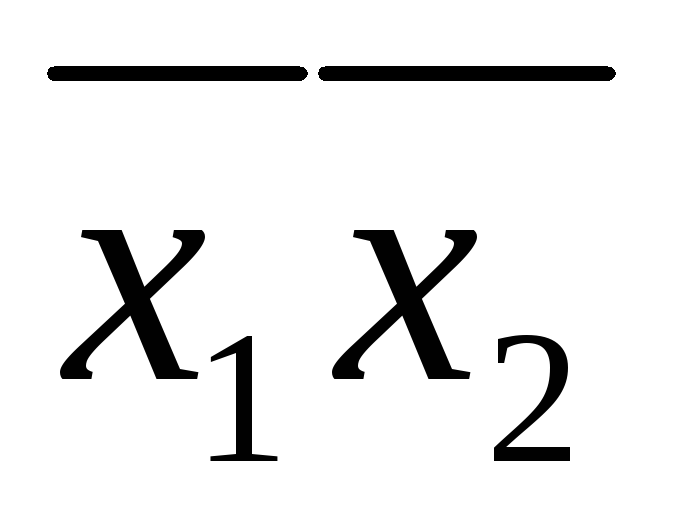
(16, 17, 18, 19, 24, 25, 26, 27) – (1, 2, 8)
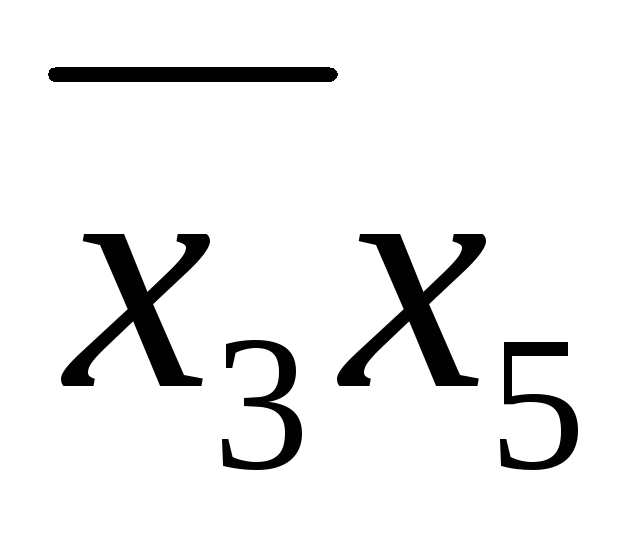
(10, 11, 14, 15) – (1, 4)

Таким образом, получим МДНФ заданной функции:

f=.