Лабораторная № 31

Федеральное агентство по образованию РФ

Санкт-Петербургский государственный электротехнический университет

Кафедра МО ЭВМ

Минимизация логических функций методом карт Карно.

Преподаватель: Красюк В.И.

Студент гр. 4351 Кузьменко А.

Санкт-Петербург

2008

Часть 4. Минимизация логических функций методом карт Карно.

Одним из способов задания и представления логических функций является карта Карно (диаграмма Вейча). На этом представлении основан один методов минимизации логических функций. Этот метод является удобным и наглядным только для функций с количеством переменных не более пяти.

Карта Карно (диаграмма Вейча) представляет собой развертку гиперкуба на плоскости. Каждый ячейка имеет четыре соседние, элементы в которых отличаются лишь в одном разряде, как и в гиперкубе. Карте Карно соответствует циклический код Грея, в котором каждая следующая комбинация отличается от предыдущей значением одного разряда.

При представлении функции с помощью карты Карно необходимо учитывать, что крайние столбцы и строки считаются соседними. Если свернуть карту в пространстве, соединив ее края, получим тор с такими же свойствами.

Р

x₃

ассмотрим карту Карно для функции размерности 4:

1	1		1 x2
1 x1	1
1		1	1

x₄

или:

	1	1		1
	1	1
	1		1	1

Алгоритм нахождения МДНФ по карте Карно (диаграмме Вейча) довольно прост:

1) необходимо выделить на карте контуры так, чтобы были соблюдены следующие условия:

- контуры должны содержать в ячейках внутри себя только единицы,

- контуры должны быть прямоугольными или квадратными,

- они должны включать число ячеек, равное степени 2: 1, 2, 4, 8 или 16 ячеек, например:

- крайние столбцы, крайние строки и угловые ячейки считаются соседними, то есть контуры могут быть и такими:

- каждый контур должен охватывать по возможности наибольшее число ячеек,

- контуры могут пересекаться,

- не должно быть контуров, все ячейки которых входят в другие контуры, например не должно быть следующего:

Так как все ячейки контура, охватывающего последний столбец, входят в оставшиеся два контура.

- все единицы в ячейках должны быть покрыты контурами.

Д

x₃

ля примера, приведенного выше, система контуров будет выглядеть следующим образом:

1	1		x2 1
1 x1	1
1		1	1

x₄

2) Затем необходимо по контурам составить элементарные конъюнкции, соответствующие им.

Для этого при рассмотрении контура выделяются переменные, которые постоянны в контуре, они входят в элементарную конъюнкцию, переменные же, входящие в контур вместе со своими инверсиями, исключаются из нее. Таким образом происходит склеивание конституэнт единицы, соответствующих ячейкам, входящим в контур и формируются элементарные конъюнкции. При это контур, содержащий одну ячейку будет соответствовать конъюнкции из 4-х переменных, две – из 3-х, четыре– из 2-х и восемь – из одной переменной (или инверсии).

Для рассматриваемого примера получим:

- контур в верхнем левом углу - ,

- контур в нижнем правом углу - ,

- оставшийся контур - .

Тогда МДНФ рассмотренной функции будет : f=.

Минимизация на карте Карно для функции с пятью переменными сложнее, так как такая карта представляет собой две зеркально отраженные карты 44, и при этом расположение элементов, которые можно склеивать не столь очевидно.

Р

x₅

x₅

ассмотрим такую карту (в ней пронумерованы столбцы, сама карта не заполнена):

1	2	3	4	5	6	7	8
x1
							x2

x₃

x₄

Из-за зеркального отображения соседними будут не только пары столбцов (1, 2), (2, 3), … (7, 8), (8, 1), но и следующие пары: (3, 6), (2, 7), (1, 4), (5, 8). Тогда можно будет отмечать одним контуром следующие области (единицами отмечены ячейки, входящие в один контур на каждом рисунке, также отмечены элементарные конъюнкции для каждого из контуров, схема карт соответствует вышеприведенной).

1

						1
1							1

1	1					1	1
1	1					1	1

		1	1	1	1
		1	1	1	1

1			1
1			1
1			1
1			1

		1			1
		1			1

1	1					1	1
1	1					1	1
1	1					1	1
1	1					1	1

				1			1
				1			1

1	1					1	1
1	1					1	1

1			1
1			1

	1	1			1	1
	1	1			1	1

	1	1			1	1
	1	1			1	1

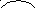
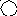
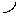
1	1					1	1