3. Дивергенция векторного поля. Теорема Гаусса–Остроградского
Определение. Пусть в пространстве задан вектор
где функции P, Q и R дифференцируемые в некоторой области D R3.
Тогда
дивергенцией
векторного поля
называется
скалярная величина, обозначаемая
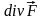и вычисляемая по формуле:
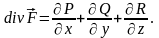
Теорема Гаусса–Остроградского
Пусть
задана замкнутая поверхность S
,
ограниченная двумя правильными по
направлению оси
OZ
поверхностям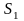и
и
,
описываемые, как
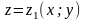и
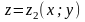соответственно. Тогда поток вектора
через
поверхность
с нормалью
,
направленной из внутренней части,
ограниченной поверхностью S
(наружу по
отношению к объёму V), вычисляется по формуле:
В векторной форме формула ГауссаОстроградского имеет вид:
Эта
формула Гаусса–Остроградского
связывает поток вектора
через замкнутую поверхность S,
ориентируемую
вектором нормали
,
направленный наружу по отношению к
объёму V,
заключенному внутри поверхности S,
с
тройным интегралом по объему V
от
.
Если вектор
является вектором скорости жидкости,
протекающей через объём V,
то
интеграл даёт количество жидкости,
вытекающей из объёма V
через поверхность S
в единицу времени. Если жидкость втекает
в объём V,
то тройной интеграл получается
отрицательным, так как
.
Если
во всех точках объёма V,
то поток вектора
равен
0. Это означает, что количество втекающей
жидкости и вытекающей из объёма V
одинаковое.
Пример.
Определить поток вектора
через внешнюю сторону сферы
.
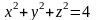Найдём
;
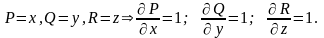Следовательно
Ответ:
.
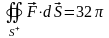4. Ротор (вихрь) векторного поля. Теорема Стокса
Определение.
Ротором
(или вихрем)
векторного поля
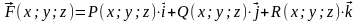называется вектор, который в каждой
точке дифференцируемости поля обозначается
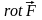и вычисляется следующим образом:
.
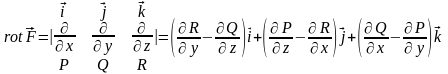Теорема Стокса
Пусть в пространстве задан замкнутый гладкий контур C, являющийся границей поверхности S, заданной непрерывно дифференцируемой функцией. Ориентация поверхности S согласуется с направлением обхода контура C «по правилу винта»: вектор нормали в каждой точке поверхности S направлен так, что если смотреть с конца вектора, то обход контура C наблюдается против часовой стрелки (в этом случае направление вектора нормали считается положительным). Тогда справедлива формула:
Эта формула устанавливает связь между криволинейным интегралом II рода по замкнутому контуру, т.е. циркуляцией вектора , с поверхностным интегралом II рода от векторного поля по поверхности S, ориентированной с обходом контура C «по правилу винта», т.е. с потоком вектора по поверхности, натянутой на контур C.
В векторной форме формула Стокса имеет вид:
Замечание 1. Если рассматривать формулу Стокса в плоском случае (т.е. если z=0), то получается формула Грина. Значит, формула Грина является частным случаем формулы Стокса. Замечание 2. Из теоремы Стокса следует, что потоки через любые две поверхности, имеющие общий «край», равны.
Пример.
Применяя формулу Стокса, вычислить
,
если контур C:
(окружность
на плоскости OXY).
Найдём
вектор
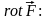
Итак:
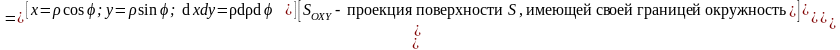
Ответ:
