34.Критерії згоди. Критерій згоди Пірсона перевірки гіпотези про довільний закон розподілу. Перевірки гіпотези для розподіл Пуасона генеральної сукупності.

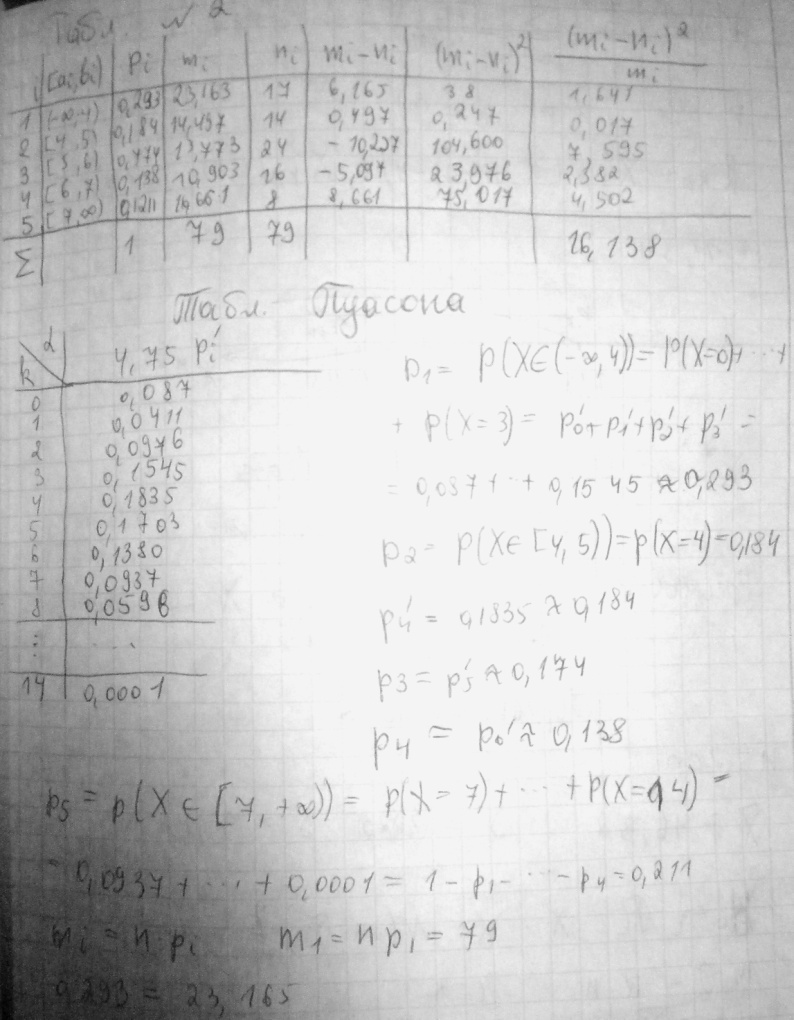
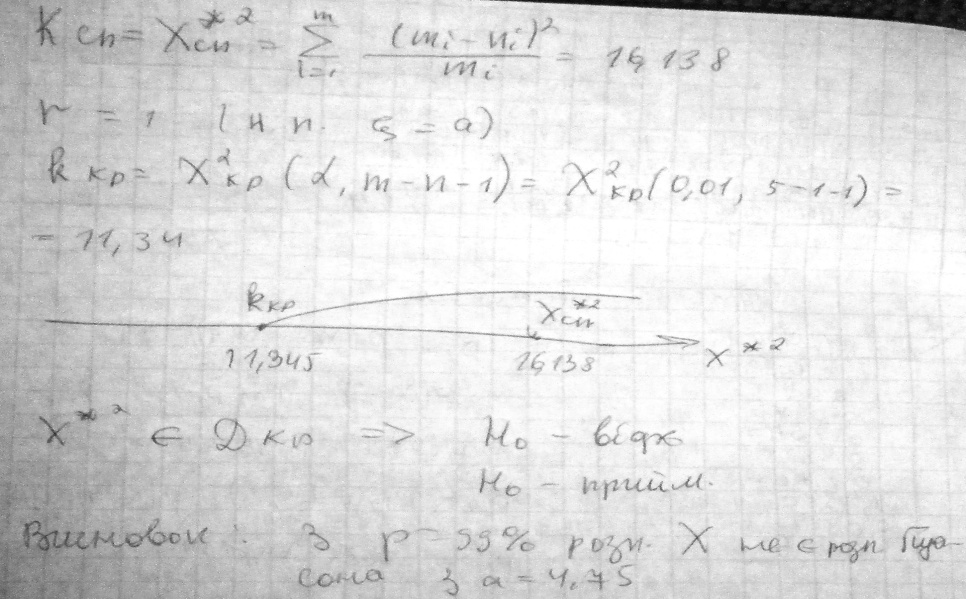
35.Критерії згоди. Критерій згоди Пірсона перевірки гіпотези про довільний закон розподілу. Схема перевірки гіпотези про нормальний розподіл генеральної сукупності.

Кількість параметрів нормального розподілу (невідомих параметрів два – ). При обчисленнях замість використовуємо знайдені раніше незсунені оцінки цих числових характеристик: , .

Нульова гіпотеза: має нормальний розподіл із параметрами .

Альтернативна: не має нормального розподілу із параметрами .

Для перевірки нульової гіпотези використовуємо критерій згоди Пірсона. Для цього треба числову вісь розбити на деяку кількість інтервалів, що не перетинаються, емпірична частота попадання в кожен із яких не мала. Використовуємо дискретний варіаційний ряд, розділивши його на інтервали , але однією з умов обґрунтованого застосування критерію згоди Пірсона є те, що інтервали, які містять малу кількість елементів, об’єднують із сусідніми, щоб у кожному з них було не менше ніж 5 елементів. об’єднані (емпіричні) частоти – у стовпчику . У результаті об’єднання кількість інтервалів .

При застосуванні критерію згоди Пірсона порівнюються емпіричні та теоретичні частоти нормально розподіленої випадкової величини. Для знаходження теоретичних частот , заповнимо наступні 4 стовпчики Додатку У. У 5-му та 6-му стовпчику підраховано відповідні значення нормованої величини . Теоретичні частоти у 7-му стовпчику є різницею значень 6-го та 5-го стовпчиків. Наступний стовпчик - стовпчик теоретичних частот, які визначаються за формули: при великих має розподіл Пірсона степенями свободи. Спостережуване значення критерію знайдено як суму останього стовпчика таблиці 5: . Критична область – правобічна. Критичну точку знайдемо за таблицею розподілу Пірсона:

- отже, приймається.

36.Факторний аналіз. Основні гіпотези, які перевіряються у факторному аналізі. Особливості перевірки цих гіпотез при рівній кількості спостережень на різних рівнях фактору.

39. Критерій Кочрена. Приклад його застосування. Як слід діяти, якщо гіпотеза про рівність дисперсій не підтвердилася.

За вибіркою із генеральної сукупності перевіримо гіпотезу про рівність математичних сподівань на трьох рівнях фактора (фактор – розподіл по магазинах) при рівні значущості .

Нульова гіпотеза , де - відповідно математичні сподівання генеральних сукупностей – прибутків по трьох магазинах. Для того, щоб застосувати критерій Фішера для перевірки цієї гіпотези, треба впевнитися, що дисперсії цих генеральних сукупностей із заданим рівнем значущості рівні.

Перевіримо гіпотезу , де - відповідно дисперсії генеральних сукупностей . Альтернативна гіпотеза існує .

Для перевірки гіпотези можна скористатися критеріями Бартлетта Кочрена. Бажаніше застосувати критерій Кочрена, тому що критичні точки цього розподілу точно знайдено(див. додаткову таблицю), а розподіл Бартлетта відомий лише наближено. У нашому випадку, оскільки кількість спостережень на різних факторах однакова, можна застосувати критерій Кочрена.

Відомо, що коли правильно, кількість спостережень на всіх рівнях фактора (у нас ), то випадкова величина має розподіл Кочрена з степенями свободи і кількістю вибірок (тут - виправлені вибіркові дисперсії на всіх рівнях–фактора).

При даній альтернативній гіпотезі критична область правобічна. Критичну точку шукаємо за таблицею розподілу Кочрена:

спостережуване значення критерію: .

, гіпотеза про рівність дисперсій на всіх рівнях фактора підтвердилась.

Гіпотеза про рівність дисперсій підтвердилась, тому переходимо до перевірки гіпотези про рівність математичних сподівань за допомогою критерію Фішера. У нашому випадку на всіх рівнях фактора однакова кількість спостережень , тому для обчислення факторної та залишкової дисперсії використовуємо спрощені формули.

Якщо нульова гіпотеза справедлива, то випадкова величина 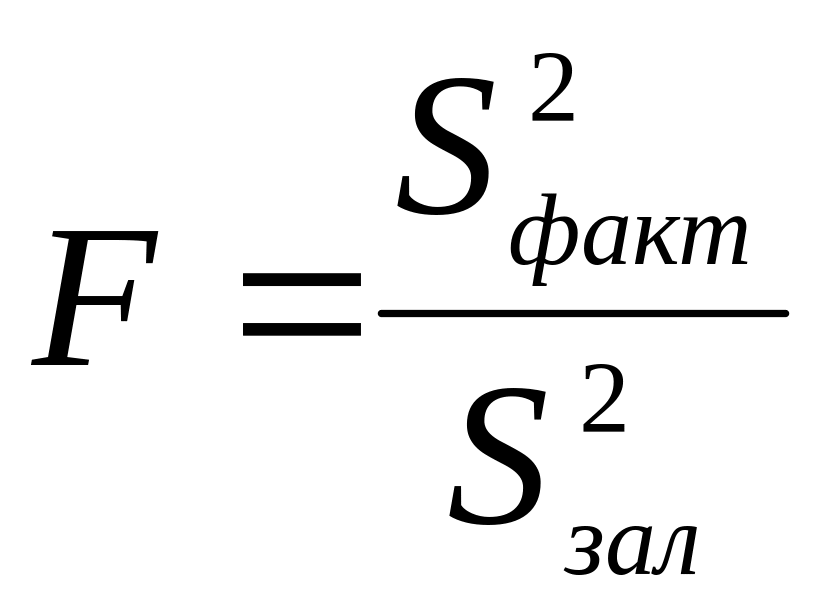має розподіл Фішера з та степенями свободи. ;

Для визначення підраховуємо додаткові величини , , :

; ;

Факторна дисперсія визначається так:

Знайдемо спостережуване значення критерію Фішера: .

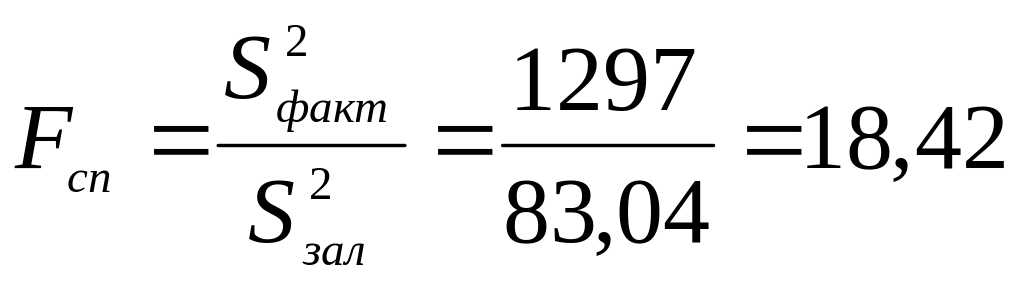При даній альтернативній гіпотезі критична область – правобічна, критична точка визначається за таблицею розподілу Фішера: .

отже, спостережуване значення попадає в критичну область, нульову гіпотезу відхиляємо, приймаємо альтернативну гіпотезу.

Знаходимо середнє значення з усіх вибіркових середньоарифметичних по вибірках , отримуємо . Тепер знаходимо

, де - номер варіанта

Тепер знаходимо спостережуване значення критерію

При даній альтернативній гіпотезі критична область – правобічна, критична точка визначається за таблицею розподілу Фішера:

отже, спостережуване значення не попадає в критичну область, нульову гіпотезу приймаємо.

Тепер треба виокремити рівень фактора, вибіркове середнє значення по якому значно відрізняється від середніх значень на інших рівнях. Як видно, вибіркові середні для перших двох рівнів схожі, а третій суттєво відрізняється від обох, причому в більшу сторону, тому висуваємо додаткові гіпотези:

а) перша – для перевірки того, чи рівні математичні сподівання на всіх рівнях фактора, крім того, який виключений із розгляду, гіпотеза , .

Оскільки рівнів фактора лишилось два, дану гіпотезу не обов’язково перевіряти методами факторного аналізу, а можна, наприклад, за допомогою Т-критерію перевірки гіпотези про рівність математичних сподівань, отже, аналогічно наведеному вище

При висунутій альтернативній гіпотезі шукаємо симетричну двобічну критичну область, тоді:

,тобто гіпотеза про рівність математичних сподівань на перших двох рівнях фактора підтвердилась.

б) друга – для перевірки того, чи той рівень фактора ми виключаємо з розгляду і в яку сторону відрізняються математичні сподівання на виділеному рівні фактора від інших: , .

При висунутій альтернативній гіпотезі критична область лівобічна:

, тобто гіпотеза про рівність математичних сподівань на першому та третьому рівнях фактора не підтверджується і приймається .