36. Частное и полное приращение функции. Частные производные функции нескольких переменных. Градиент.

Пусть х->дельта х

Тогда z->дельта z

Дельта z=а(х+дельта х,у)-f(x,y) –часное приращение функции z=f(x,y) по х

(аналогично по у)

Выражение  называется полным приращением функции f(x, y) в некоторой точке (х, у), где a1 и a2 – бесконечно малые функции при Dх -> 0 и Dу -> 0 соответственно.

Частной производной функции z=f(x,y) по переменной х над пределом отношения частного приращения дельта z к приращению аргумента дельта х

Zx’=dz/dx=lim дельта хZ/дельта х

Дельта х->0

Градиент функции – вектор составленный из частных производных функций (gradz)

Частным дифференциалом по х функции z=f(x,y) называется произведение частной производной по х на приращение аргумента дельта х (аналогично по у)

Dxz=Zx-дельта х

Полным приращением дифференциала функции z=f(x,y) называется главная часть полного приращения функции дельта z вызванного приращением аргумента х и у 38. Дифференцирование сложной функции нескольких переменных.

Дельта z=f(х+ дельта х,у+дельта у)-f(x,y) 39. Производные высших порядков для функции 2-х переменных. Теорема о смешанных производных.

Z=f(x,y)

Zx’,Zy’-непрерывные и дифференцируемые

Теорема: если обе смешенные производные d²z/dxdy и d2z2/dydx определены в окресности некоторой (.)М0(х0,у0) и непрерывна в этой точке, то они равны друг другу:Zxy’’=Zyx’’

40. Экстремумы функции 2-х переменных. Необходимое условие существования экстремум.

Функция z=f(x,y) имеет в (.)М0(х0,у0) экстремум если такая окрестность в (.)М0, для всех точек которой f(x0,y0)>или <f(x,y)

Если в (.)М0 (х0,у0) дифференцируемая функции z=f(x,y) имеет экстремум,то ее частные проиводные Zx’ и Zy’ в этой точки необходимо = 0

Zx’ dz/dx=0 и Zy’dz/dy=0 в (.)М0

41. Достаточное условие существования экстремума для функции 2-х переменных..

Составим определитель из частных производных: производных 2го порядка

Определитель=|Zxx’’ Zxy’’|

|Zxy’’ Zyy’’|

Если определитель вычисленный в критической точке М0(х0,у0)больше 0,то в точке М0 есть экстремум при Zxx’’>0-максимум, Zxx’’<0-минимум

Если определитель меньше 0, то в точке М0(х0,у0) экстремума нет, если определитель =0, то ничего определенного сказать нельзя 42. Первообразная и неопределенный интеграл.

Функция F(x) называется первообразной от функции f(x), если для нее выполняется равенство

F ‘(x)=f(x)

Т]Если F(x) первообразная от f(x), то F(x)+C,где С-const,тоже первообразная от f(x)

Множество первообразных вида F(x)+C от функции f(x) называется неопределенным интегралом : интегралf(x)dx=F(x)+C 43. Свойства неопределенного интеграла.

1.(интеграл f(x)dx)’=f(x)-производная от неопределенного интеграла = подынтегральному выражению

2.d интеграл f(x)dx=f(x)dx –дифференциал от интеграла равен подынтегральному выражению

3.интеграл dF(x)=F(x)+C –интеграл от дифференциала взаимно уничтожаются с прибавление производной постоянной

4.интеграл с*f(x)dx=C= интеграл f(x)dx, C-const –константу можно выносить за знак неопределенного интеграла

5.интеграл(f1(x)+-f2(x))dx= интеграл f1(x)dx+- интеграл f2(x)dx – интеграл от алгебраической суммы функции = алгебраической сумме интегралов этих функций

44. Методы интегрирования. Непосредственное интегрирование. Введение функции под знак дифференциала. Метод подстановки. Интегрирование по частям.

Непосредственное интегрирование- это интегрирование с помощью выполнения алгебраических преобразований, использование свойств неопределенного интеграла и таблицы интегралов

Метод подведения под знак дифференциала основан на равенстве . То есть, главной задачей является приведение подынтегральной функции к виду .

Замена переменной:х=u(t) или t=u^-1

Если подынтегральная функция состоит из сомножителей в этом случае удобно применять функцию интегрирования частями, а именно:

Интеграл u*dw=u*w-интеграл w-du 45. Интегрирование рациональных дробей .Интегрирование простейших дробей.

Рациональной дробью называется выражение вида:

R(x)=Pn(x)/Qm(x), где Pn – многочлен степени n,Qm-многочлен степени m

Если степень числителя меньше степени знаменателя, то дробь правильная, если степень числителя больше степени знаменателя- неправильная

Интеграл R(x)dx

Перед интегрированием неправильных дробей следует выделить целую и дробную часть, делением столбиком

Интегрирование простейших дробей первого типа

Для решения этой задачи идеально подходит метод непосредственного интегрирования:

Интегрирование простейших дробей второго типа

Для решения этой задачи также подходит метод непосредственного интегрирования:

Интегрирование простейших дробей третьего типа

Для начала представляем неопределенный интеграл в виде суммы: 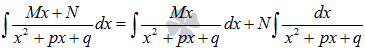Первый интеграл берем методом подведения под знак дифференциала: Поэтому, У полученного интеграла преобразуем знаменатель: Следовательно, Формула интегрирования простейших дробей третьего типа принимает вид:

Интегрирование простейших дробей четвертого типа

Первый шаг – подводим под знак дифференциала: Второй шаг – нахождение интеграла вида . Интегралы подобного вида находятся с использованием рекуррентных формул. 46. Интегрирование простейших иррациональных выражений.

Используя метод непосредственного интегрирования, достаточно просто находятся неопределенные интегралы вида , где p – рациональная дробь, k и b – действительные коэффициенты.

Бывают случаи, когда уместно использование метода подведения под знак дифференциала. Например, при нахождении неопределенных интегралов вида , где p – рациональная дробь.

Достаточно часто приходится иметь дело с неопределенными интегралами вида , где p и q – действительные коэффициенты. В этом случае выделяем полный квадрат под знаком корня:

Нахождение множества первообразных иррациональных функций , где M, N, p и q – действительные коэффициенты, очень схоже с интегрированием простейших дробей третьего типа: выполняется подведение под знак дифференциала, затем выделяется полный квадрат подкоренного выражения и применяются формулы из таблицы первообразных.

еопределенные интегралы иррациональных функций вида находятся методом подстановки. В зависимости от рациональных чисел m, n и p вводят следующие новые переменные:

1. Если p - целое число, то принимают , где N - общий знаменатель чисел m и n.

2. Если - целое число, то , где N - знаменатель числа p.

3. Если - целое число, то вводят новую переменную , где N - знаменатель числа p.

47. Интегрирование тригонометрических функций. Универсальная тригонометрическая подстановка.

Из таблицы первообразных сразу заметим, что и . Метод подведения под знак дифференциала позволяет вычислить неопределенные интегралы функций тангенса и котангенса:

Вычисление неопределенных интегралов типа  сводится к вычислению интегралов от рациональной функции подстановкой tg = t , х=2 arctgx , которая называется универсальной. В результате этой подстановки имеем

tg x/2= t , x =2 arctgt , sinx = 2t/1+t², cosx =1-t² /1+t² , dx = 2dt/1+t².

48. Интегральные суммы. Понятие определенного интеграла.

Определенным интегралом называется придел интегральной суммы Римана

limSn = limⁿ_{n->бесконечности} Σf(li)*дельта xj=^b_aинтеграл f(x)dx

^{n->бесконечности n->бесконечности}

Определенный интеграл, где а -нижний придел, в-верхний придел.Придел не зависит не от способа разбивания отрезка [а,в] на элементарные части, не от выбора точки li на каждой из этих элементов частей

49. Связь неопределенного интеграла с определенным. Формула Ньютона-Лейбница.

Формула Н-Л выражает связь определенного интеграла с неопределенным и имеет вид:

^в_аинтеграл f(x)dx=F(b)-F(a)

^b_aинтеграл f(x)dx = F(x)|^b_{a =}F(b)-F(a) 50. Свойства определенного интеграла.

1.интеграл с равными приделами =0

2.От перестановки пределов интеграл меняет знак

3.Постояный множитель можно выносить за знак определенного интеграла

4.Аддитивность:если (.)С принадлежит (а,в), то

^b_a интеграл f(x)dx= ^c_a интеграл f(x)dx+ ^b_cинтеграл f(x)dx

5.интеграл от алгебраической суммы функций = алгебраической сумме интегралов этих функций

6.Производная определенного интеграла по переменному пределу = подынтегральной функции 51. Вычисление определенного интеграла по частям. Замена переменной в определенном интеграле.

По частям: ^в_аинтеграл u*dw=u*w|^b_a-^b_aинтеграл w*du

Замена:

^b_aинтеграл f(x)dx=|x=u(t),где|

|t принадлежит [t1,t2]|

|dx=u(t)dt| =^t2_t1интеграл f(u(t)) u’(t)dt

|x|a|b| |

|t|t1|t |

52. Несобственные интегралы с бесконечными пределами (1-го рода). Определение. Вычисление. Признаки сходимости.

Несобственным интегралом от функции f(x) называется придел

lim ^в _аинтеграл f(x)dx= ^{бесконечность}_аинтеграл f(x)dx

в-> бесконечности

Если lim в выражение lim ^в _аинтеграл f(x)dx= ^{бесконечность}_аинтеграл f(x)dx = конечному числу, то говорят что несобственный интеграл сходится

Если lim не существует или равен бесконечности, то говорят что интеграл расходится

^в_{-бесконечность}интеграл f(x)dx= lim^в_а интеграл f(x)dx

а->- бесконечности

^{бесконечность}_{-бесконечность}интеграл f(x)dx= ^c_{-бесконечность} интеграл f(x)dx + ^{бесконечность}_синтеграл f(x)dx 53. Несобственные интегралы от разрывных функций (2-го рода). Определение. Вычисление. .

Пусть функция f(x) не является ограниченной в окрестности точки b, но при любом достаточном малом е>0 является ограниченной и интегрируемой на интервале [a,b-e]. Тогда если существует придел

Lim^b-e_aинтеграл f(x)dx, то этот придел называется не собственным интегралом 2го рода

^b_aинтеграл f(x)dx= lim^b-e_aинтегралf(x)dx

e->0

^b_aинтегралf(x)dx=^c_aинтегралf(x)dx+ ^b_cинтеграл f(x)dx 54. Числовые ряды. Основные понятия. Необходимый признак сходимости

числовой последовательностью {а_n} называется множество значений натуральных чисел и рядов перенумерованный и расположенный в порядке возрастания рядов

бесконечность

а1+а2+…+аn= Σan –числовой ряд

n=1

если сумма ряда конечное число, то говорят, что ряд сходится, если сумма ряда равна бесконечности или не существует, то говорят, что ряд расходится

числовые ряды: с неотрицательными членами и знакопеременные и знакочередующие

Необходимый признак:

Если ряд сходится, то общий член ряда an стремится к 0, т.е. liman=0

n->0

Замечание: у необходимого признака сходимости, есть обратная сторона – достаточный признак расходимости

Если общий член ряда не стремится к 0, при n стремящийся к бесконечности, то ряд расходится 55 .Достаточные признаки сходимости рядов с неотрицательными членами:признаки Даламбера и Коши.

Признак Даленбера

^{бесконечность}_n=1 Σan,an>=0,D=lim an+1/an

n-> бесконечности

придел отношения соотношения последующего члена ряда к предыдущему

D>1-сходится

D<1-расходится

D=1 признак не работает

Признак Коши:

^{бесконечность}_n=1 Σan, an>=0, C=lim ⁿкорень из an

n-> бесконечности

С>1- расходится

С<1- сходится

С=1- не работает