5. Первообразная функция и ее свойства. Неопределенный интеграл, его свойства, геометрический смысл.

Первообразной функции f(x) на промежутке (a; b) называется такая функция F(x), что выполняется равенство F’(х)= f(х) для любого х из заданного промежутка.

Все множество первообразных функции f(x) называется неопределенным интегралом этой функции и обозначается .

Подынтегральное выражение представляет собой дифференциал функции f(x).

свойства неопределенного интеграла (свойства первообразной).

1.

Производная результата интегрирования равна подынтегральной функции.

2.

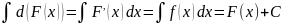
Неопределенный интеграл дифференциала функции равен сумме самой функции и произвольной константы.

3.

Коэффициент можно выносить за знак неопределенного интеграла.

4.

Неопределенный интеграл суммы/разности функций равен сумме/разности неопределенных интегралов функций.

Геометрический смысл неопределённого интеграла.

Пусть задан неопределённый интеграл F(х) + С для функции f(х) в некотором интервале. При фиксированном значении С = С₁ получим конкретную функцию у₁=F(х)+С₁, для которой можно построить график; его называют интегральной кривой. Изменив значение С и положив С = С₂, получим другую первообразную функцию С соответствующей новой интегральной кривой.

6. Теорема о существовании неопределенного интеграла. Таблица основных интегралов. Основные правила интегрирования.

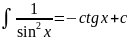
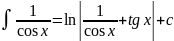
Основные правила интегрирования

1) Если 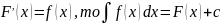, где с – произвольная постоянная.

2) , где А – постоянная величина

3)

4) Есл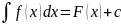и и ,

то

В частности

7. Метод непосредственного интегрирования. Теорема об инвариантности формул интегрирования.

Метод интегрирования, при котором интеграл путём тождественных преобразований подинтегральной функции (или выражения) и применения свойств неопределённого интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием.

Теорема об инвариантности формул интегрирования: Всякая формула интегрирования сохраняет свой вид при подстановке вместо независимой переменной любой дифференцируемой функции

8. Метод замены переменных в неопределенном интеграле.

Для упрощения вычисления интеграла часто удобно выполнить замену переменной. Переход от x к новой переменной u описывается выражением

где x=g(u) - подстановка. Соответственно, обратная функция u=g^-1(x) описывает зависимость новой переменной от старой.

9. Метод интегрирования по частям.

Метод интегрирования по частям позволяет свести исходный неопределенный интеграл к более простому виду либо к табличному интегралу.

Формула интегрирования по частям следующая

.

10. Простейшие дроби и их интегрирование.

виды простейших дробей:

Дробь первого порядка

Дробь второго порядка

Дробь третьего порядка

Дробь четвертого порядка

11. Дробно-рациональные функции, правильные и неправильные дроби. Разложение правильной дроби на простейшие. Интегрирование дробно-рациональных функций.

Дробно-рациональное выражение – это дробь, числителем и знаменателем которой являются многочлены с рациональными (целыми) коэффициентами.

Рациональная дробь называется правильной, если порядок знаменателя больше порядка числителя, и неправильной, если наоборот

СМ (10)

Любую рациональную функцию можно представить в виде где S, P, Q - многочлены, степень P < степени Q.

После разложения P(x)/Q(x) на элементарные дроби интегрирование рациональной функции сводится к интегрированию простейших рациональных функций.

12. Интегрирование выражений, зависящих от тригонометрических функций. Универсальная подстановка.

При нахождении интегралов от тригонометрических функций используется ряд методов:

Использование тригонометрических формул

Понижение степени подынтегральной функции

Метод замены переменной

Универсальная тригонометрическая подстановка

13. Интегрирование простейших иррациональных функций.

Для интегрирования иррациональной функции, содержащей используется подстановка

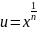
14. Определенный интеграл как предел интегральной суммы. Теорема существования.

15. Задачи, приводимые к определенному интегралу. Геометрический смысл определенного интеграла.

Задача о пройденном пути. Требуется найти путь, пройденный движущейся по прямой точкой за отрезок времени , если известен закон изменения мгновенной скорости v=v(t).

Задача о площади криволинейной трапеции.

Пусть требуется найти площадь плоской фигуры ,ограниченной графиком функции у=f(х), непрерывной и неотрицательной на отрезке [a;b], и отрезками прямых .

Геометрический смысл определенного интеграла

определенный интеграл для непрерывной и неотрицательной функции y=f(x) представляет собой в геометрическом смысле площадь соответствующей криволинейной трапеции.

То есть, вычислив интеграл , мы найдем площадь фигуры, ограниченной линиями y=f(x), y=0, x=a и x=b.