1.4 Построение графиков

В нашем случае:

a≈ 3,7689;

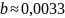
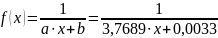
График 1 – График функции

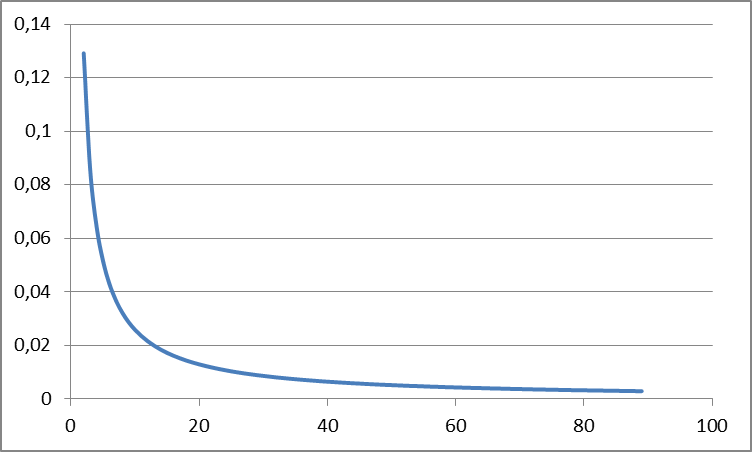
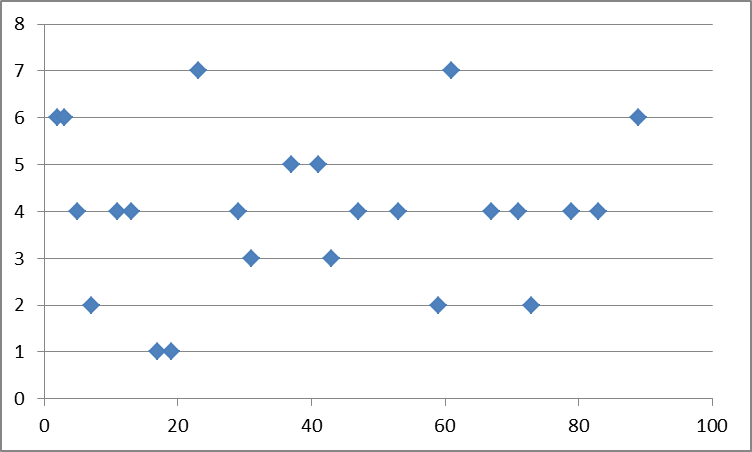
График 2 – Исходные данные

2. Определение показателей описательной статистики

2.1 Определение описательной статистики

Описательная статистика позволяет обобщать первичные результаты, полученные при наблюдении или в эксперименте. Процедуры здесь сводятся к группировке данных по их значениям, построению распределения их частот, выявлению центральных тенденций распределения (например, средней арифметической) и, наконец, к оценке разброса данных по отношению к найденной центральной тенденции.

Цель описательной (дескриптивной) статистики — обработка эмпирических данных, их систематизация, наглядное представление в форме графиков и таблиц, а также их количественное описание посредством основных статистических показателей.

2.2 Показатели описательной статистики

Для этого придуманы описательные или дескриптивные статистики:

• Минимум;

• Максимум;

• Дисперсия;

• Cтандартное отклонение;

• Cреднеквадратическое отклонение;

• Размах.

Минимум и максимум — это минимальное и максимальное значения переменной.

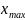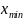В нашем примере: = 89, = 2

Разность между максимумом и минимумом называется размахом вариации. Все данные выборки расположены в промежутке между минимумом и максимумом. Эти показатели как бы очерчивают границы выборки.

Размах вариации вычисляется по формуле:

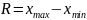
Дисперсия – в математической статистике и теории вероятностей, наиболее употребительная мера рассеивания, т.е. отклонения от среднего. Дисперсия находится по формуле:

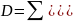
Среднеквадратическое отклонение – в теории вероятностей и статистике наиболее распространенный показатель рассеивания значений случайной величины относительно ее математического ожидания. Оно равно корню квадратному из дисперсии случайной величины. Среднеквадратическое отклонение используют при расчёте стандартной ошибки среднего арифметического, при построении доверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами.

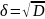
Дисперсия и среднеквадратическое отклонение выборки являют собой меру изменчивости переменной и характеризуют степень разброса данных вокруг центра. При этом среднеквадратическое отклонение является более удобным показателем в силу того, что имеет ту же размерность, что и собственно исследуемые данные.

2.3 Пример процедуры «Статистика»

Procedure Pokazateli;

begin

xmax:=x[1];

for i:=1 to n do

begin

if x[1]>xmax then

xmax:=x[i];

End;

xmin:=x[1];

for i:=1 to n do

begin

if x[i]<xmin then

xmin:=x[i];

End;

R:=xmax-xmin;

writeln('R=',R:6:4);

D:=0;

for i:=1 to n do

begin

D:=D+sqr(x[i]-Sx);

end;

D:=(sqr(x[i]-Sx))/(n-1);

G:=sqrt(D);

writeln('xmin=',xmin:6:4);

writeln('xmax=',xmax:6:4);

writeln('D=',D:6:4);

writeln('G=',G:6:4);

End;

Function f(x:real):real;

begin

F:=1/((a+b*x)*(a+b*x));

End;

3 Вычисление определенного интеграла

3.1 Метод Симпсона

Этот метод более точный по сравнению с методами прямоугольников и трапеций.

Формула Симпсона (также Ньютона-Симпсона) относится к приёмам численного интегрирования. Получила название в честь британского математика Томаса Симпсона (1710—1761).

Суть приёма заключается в приближении подынтегральной функции на отрезке [a, b] интерполяционным многочленом второй степени p2(x), т.е. приближение графика функции на отрезке параболой. Метод Симпсона имеет порядок погрешности 4 и алгебраический порядок точности 3.

Геометрически иллюстрация формулы Симпсона состоит в том, что на каждом из сдвоенных частичных отрезков заменяем дугу данной кривой дугой графика квадратного трехчлена.

Для непрерывной функции y=f(x) на [a,b] погрешность формулы парабол (Симпсона) пропорциональна h4.А это значит, что уменьшение шага в два раза ведет к уменьшению погрешности формулы Симпсона в 16 раз.

По формуле Симпсона при некотором шаге h вычисляют интеграл. Затем шаг увеличивают вдвое и опять вычисляют интеграл. Второе, более грубое вычисление интеграла служит для оценки точности первого, более точного. Все цифры первого и второго вычислений совпадающие в результате, а также первая неточная цифра более точного результата считаются верными. Например, если более точное вычисление число 1,4673, а второе - 1,4657, то 1,467 - верное значение интеграла (в нем 4-значащие цифры - верные).

Для проведения более грубого расчета никаких других подготовительных работ не требуется. Значения xi и y(xi) берутся через одно. Следует только учесть, что при первом (более точном) расчете необходимо выбрать такое число точек разбиения, которое кратно 4 т.е. делится на четыре. Если при выбранном исходном шаге h необходимая точность результата не достигнута, то проводят третье, четвертое вычисления с шагом равным половине исходного и т.д.

Разобьем отрезок интегрирования [a; b] на 2 × n равных частей длины. Обозначим точки разбиения x0=a; x1=x0+h, ... , xi=x0+i× h, ..., x2n=b. Значения функции f в точках xi обозначим yi, т.е. yi=f(xi). Тогда согласно методу Симпсона:

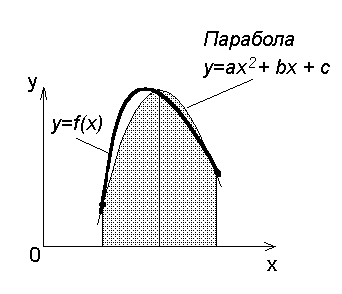
Рисунок 1 - Метод парабол (метод Симпсона)

Геометрический смысл формулы Симпсона: площадь криволинейной трапеции под графиком функции f(x) на отрезке [a, b] приближенно заменяется суммой площадей фигур, лежащих под параболами по рисунку 1.