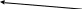4 Структуры управления. Взаимодействия акторов

4.1. Нарисуйте направленный граф. 1) Сколько двух шаговых путей из n2 в n3?. 2) Если вершины – это группы или люди, а стрелки – предложения или указания, можно ли считать эту структуру иерархией? 3) Если да, то кто руководитель и его заместитель?

	n1	n2	n3	n4	n5
n1	0	1	0	1	0
n2	0	0	0	0	1
n3	0	0	0	1	0
n4	0	1	1	0	0
n5	1	1	1	1	1

Вариант ответа: 1) Только один путь n2- n5- n4. 2) Да. 3) n5 – это руководство: совет директоров или генеральный директор; n1 – исполнительный директор и руководит головным отделом n4. Пояснение. n2 – это отдел сбыта и планово-договорной, через них подписываются договора у директора; n3 и n4 – это основные производственные или аналитические отделы на этой фирме, n4 – головной. Через руководство n5 также идут также распоряжения на зарплату и отпуска.

4.2. Заполните матрицу представления заданного направленного графа. Какого типа функции может выполнять организация 4?

	n1	n2	n3	n4	n5	n1 n2 n4 n5 n3
n1
n2
n3
n4
n5

Вариант ответа: Это может быть медицинская организация, таможня, предприятие по утилизации отходов, государственные склады, архивы, библиотеки. Это общественные, государственные или частные некоммерческие организации исполняющие заказы.

4.3. Нарисуйте направленный граф. Можно ли интерпретировать его как связи правительства с министерствами?

	n1	n2	n3	n4	n5
n1	1	1	1	1	1
n2	1	0	0	0	0
n3	1	0	0	0	0
n4	1	0	0	0	0
n5	1	0	0	0	0

Вариант ответа: Если n1 – это Правительство – центральный орган власти РФ, а n2- n5 – это Министерства – органы исполнительной власти, то можно. Такая интерпретация возможна, потому, что Министерства, как органы исполнительной власти, самостоятельны в осуществлении своих полномочий, установленных федеральными законами, актами Президента РФ и Правительства РФ. При осуществлении этих полномочий  Министерство непосредственно взаимодействует с другими органами государственной власти и органами местного самоуправления

4.4. К какому типу связей и организаций можно отнести эту сеть на рис.1?

Расположите вершины по кругу и восстановите графический образ. Определите наличие и число трехшаговых путей

	1	2	3	4	5	6	7	8	9	10	11	12	13
1	0	0	1	0	0	0	0	0	0	0	0	0	0
2	0	0	1	0	0	0	0	0	0	0	0	0	0
3	1	1	0	1	0	0	0	0	0	1	0	0	0
4	0	0	1	0	0	1	0	0	0	1	0	0	0
5	0	0	0	0	0	0	1	0	0	1	0	0	0
6	0	0	0	1	0	0	0	0	0	1	0	0	0
7	0	0	0	0	1	0	0	1	1	0	0	0	0
8	0	0	0	0	0	0	1	0	0	0	0	0	0
9	0	0	0	0	0	0	1	0	0	0	0	1	0
10	0	0	1	1	1	1	0	0	0	0	1	1	0
11	0	0	0	0	0	0	0	0	0	1	0	0	1
12	0	0	0	0	0	0	0	0	1	1	0	0	0
13	0	0	0	0	0	0	0	0	0	0	1	0	0

Рис. 1 Матрица представления графа. Голубым цветом выделены связи вершин.

Ответы: Мы классифицируем это сообщество как сеть или неориентированный граф. Число трех-шаговых путей представлено на рис 2. в матрице третьей степени М³. Цифры в ячейках этой матрицы означают число трех-шаговых путей. Наличие более коротких путей для этих ячеек(пары вершин) отображено с помощью цвета.

	1	2	3	4	5	6	7	8	9	10	11	12	13
1	0	0	4	1	1	2	0	0	0	1	1	1	0
2	0	0	4	1	1	2	0	0	0	1	1	1	0
3	4	4	2	7	1	2	1	0	1	10	1	1	1
4	1	1	7	4	2	5	1	0	1	8	2	2	1
5	1	1	1	2	0	1	4	0	1	7	0	1	1
6	2	2	2	5	1	2	1	0	1	8	1	1	1
7	0	0	1	1	4	1	0	3	4	1	1	1	0
8	0	0	0	0	0	0	3	0	0	1	0	1	0
9	0	0	1	1	1	1	4	0	0	1	1	3	0
10	1	1	10	8	7	8	1	1	1	4	7	7	0
11	1	1	1	2	0	1	1	0	1	7	0	0	2
12	1	1	1	2	1	1	1	1	3	7	0	0	1
13	0	0	1	1	1	1	0	0	0	0	2	1	0

Рис. 2. Матрица третьей степени М³

Голубым цветом выделены ячейки (пары вершин) сети, где помимо трехшаговых путей существуют прямые, одно-шаговые связи. Желтым цветом выделены пары вершин, где существуют двух-шаговые пути. Остальные ячейки (пары вершин) среди закрашенных выделены зеленым цветом. Зеленые определяют пары, для которых трех-шаговый путь наиболее короткий. Незакрашенные ячейки (где стоят нули) отображают пары вершин, которые находятся более чем в трех шагах друг от друга.

4.5. К какому типу связей можно отнести сообщество на рис.3? Постройте матрицу связей. Определите размер сети.

Рекомендации по построению матрицы сети. Двигая линейку вертикально, нумеруйте вершины по мере их попадания на вертикальную линию сверху вниз. Картинка растянута, чтобы порядок был единственно очевидным для всех студентов. Здесь 2 случая попадения вершин (акторов) на одну вертикаль. Задание: Определите размер сети.

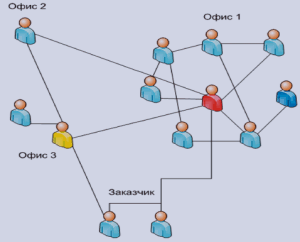
Рис. 3. Система трех офисов, с персональными коммуникациями

Решение: Порядок решения должен быть следующим 1. Построить матрицу связей и раскрасить ячейки, где есть связи. 2. Возвести матрицу во 2-ю степень. Ячейки, где стоят не нули показывают число 2-х шаговых путей, нужно раскрасить те из них, где были прямые связи в «родной» цвет. 3. Если остались ячейки, где стоят нули в М², то вычислить следующую (третью) степень матрицы, и раскрасить известные ячейки одно-шаговых и двух-шаговых путей, и так далее. 4. После исчисления матрицы М⁵ , когда на поле матрицы не останется нераскрашенных нулей, это будет означать, что размер сети 5, потому что среди кратчайших путей в сети путь в 5 шагов максимальный, то есть, не более чем пять шагов достаточно, чтобы перейти от одной вершины к другой.

4.6. Постройте матрицу представления сети на рис 4. Двигая линейку вертикально, нумеруйте вершины по мере их попадания на вертикальную линию сверху вниз. Если в сети есть «брокеры» и «мосты» определите номера вершин. Предложите интерпретацию вершин различного цвета. Определите размер сети.

Рис. 5. Сеть с разноцветными вершинами

Решение: Брокерами являются первая из желтых вершина (№ 3) и две красные (№11 и № 20). Эти вершины обладают свойством: если их убрать, то нарушится связность графа (сети). Остальные вершины таким свойством не обладают. Мостом является случай висящей вершины или «листа», где ребро, соединяет зелёную вершину с сетью. Желтые вершины, возможно, означают формальных руководителей трех групп (организаций). Если вершины – это населенные пункты, то желтые вершины - формальные региональные центры. Формальный актор или вершина-носитель может не быть одновременно лидером коммуникативности, которыми обладают другие (голубые) вершины.

4.7. Задача о мостах Кёнигсберга

Город Кенигсберг представлен в виде районов четырех автономных районов – вершин A, B, C, D, соединенных семью мостами – ребрами a, b, c, d, g, e, f.

Задача 1: можно ли пройти по всем мостам, не проходя ни по одному из них дважды?

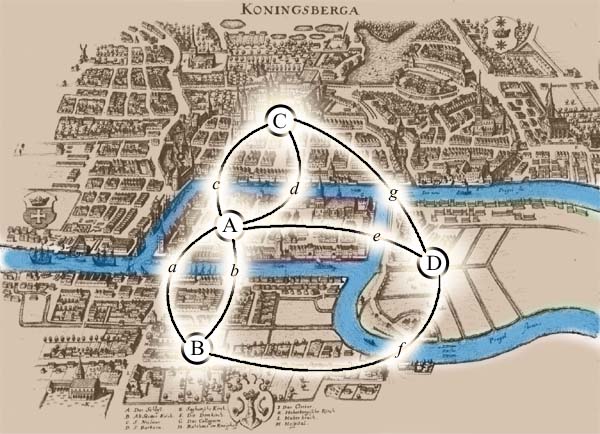
Рис. 6. Стилизованные мосты-ребра в Кёнигсберге

Задача о семи мостах была решена Эйлером. Эйлер доказал следующие теоремы:

1 ).Число нечётных вершин (вершин, к которым ведёт нечётное число рёбер) графа должно быть чётно. Не может существовать граф, который имел бы нечётное число нечётных вершин.

2). Если все вершины графа чётные, то можно, не отрывая карандаша от бумаги, начертить граф, при этом можно начинать с любой вершины графа и завершить его в той же вершине.

3. Если граф содержит более двух нечётных вершин, то обход невозможно начертить одним росчерком - решения не существует. Если граф содержит не более двух нечётных вершин, то задача имеет положительное решение.

Рис.7. Граф Кёнигсбергских мостов

У графа кёнигсбергских мостов все четыре вершины нечётные, следовательно, невозможно пройти по всем мостам, не проходя ни по одному из них дважды.

Задача 2: Заполните матрицу смежности (связей), для схемы мостов-ребер города Кенигсберга.

Задача 2: Какой мост нарисовал кайзер Вильгельм, когда его попросили решить задачу 1?

Ответы: 1) не существует, т.к. граф содержит больше двух нечетных вершин, 2) см. рис 7,

3) мост между районами С и В.

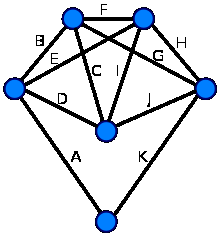
4.8. Вопрос: Существует ли Эйлеров цикл для данного на рис. 8 графа?

Ответ: Каждая вершина графа имеет чётную степень, поэтому этот граф — эйлеров. Обход рёбер в алфавитном порядке даёт эйлеров цикл

Рис.8. Граф

9