
- •Ответ №1
- •Ответ №2
- •Ответ №3
- •Ответ №5
- •Ответ №7
- •Ответ №9.
- •Ответ №10
- •Ответ№12
- •Ответ №13
- •Ответ №14
- •Ответ №16
- •Ответ №19
- •Ответ №20
- •Ответ №21
- •Ответ №22
- •Ответ №23
- •Ответ №24
- •Ответ №26
- •Ответ №27
- •Ответ №28
- •Ответ №29
- •Ответ №30
- •Ответ №32
- •Ответ №33
- •Ответ №34
- •Ответ №35
- •Ответ №36
- •Ответ №37
- •Ответ №38
- •Ответ №39
- •Ответ №40
Ответ №9.
Точки разрыва функции.
Определение: Предельные точки области определения функции, в которых эта функция не является непрерывной, называются точками её разрыва.
Примеры:
1) f(x) = [x].
x = n (целое)-точка разрыва.
2)
D(x)
=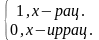 (функция Дирихле).
(функция Дирихле).
D(x)
имеет разрыва в каждой точке числовой
прямой, так как
точки а
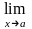 D(x)
не существует.
D(x)
не существует.
3) f(x) = x D(x)
f(x)
непрерывна в точке х
= 0, так как
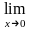 f(x)
= 0 = f(0).
f(x)
= 0 = f(0).
f(x) разрывна во всех остальных точках, так как а 0 f(x) не существует- (докажите самостоятельно).
Классификация точек разрыва.
1)Устранимый разрыв.
Точка а называется точкой устранимого разрыва функции f(x), если f(x), но
f(x) f(a) , либо в точке а функция f(x) вообще не определена.
Пример:
f(x)
=
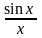 .
Будет доказано, что
=
1, но в точке х = 0 функция
не
определена, тем самым х = 0 -точка
устранимого разрыва этой функции.
.
Будет доказано, что
=
1, но в точке х = 0 функция
не
определена, тем самым х = 0 -точка
устранимого разрыва этой функции.
Если
положить f(x)
= ,
то f(x)
станет непрерывной в точке х = 0, то есть
разрыв будет устранён.
,
то f(x)
станет непрерывной в точке х = 0, то есть
разрыв будет устранён.
2) Разрыв первого рода.
Точка
а называется точкой разрыва первого
рода функции f(x),
если 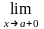 f(x)
и
f(x)
и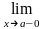 f(x),
но
f(x)
f(x).
f(x),
но
f(x)
f(x).
Пример:
f(x) = [x]
x = n (целое) - точки разрыва первого рода этой функции.
3) Разрыв второго рода.
Точка а называется точкой разрыва второго рода функции f(x), если в этой точке не существует хотя бы один из односторонних пределов.
Примеры:
1)
f(x)
=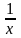 ,
х = 0 - точка разрыва второго рода, так
как f(+0)
= +,
f(-0)
= -.
,
х = 0 - точка разрыва второго рода, так
как f(+0)
= +,
f(-0)
= -.
2) Функция Дирихле D(x)-любая точка является точкой разрыва второго рода.
Функция f(x) называется непрерывной на множестве Х, если она непрерывна в каждой точке этого множества.
В частности, f(x) непрерывна на сегменте [a, b] (a < b), если она непрерывна в каждой внутренней точке сегмента, непрерывна в точке а справа и в точке b слева.
Пример:
f(x)
=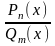 непрерывна
на любом сегменте, в точках которого
непрерывна
на любом сегменте, в точках которого
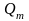 (х)
не обращается в нуль.
(х)
не обращается в нуль.
Ответ №10
Четные и нечетные функции. Функция у = f (х) называется ч етной, если для любого х из области определения функции выпол няется равенство f (- х) = f (x). Функция у = f (х) называется нечетной, если для любого х из области определения функции выполняется равенство f (- x) = - f (x). Например, у = х2, у = х4, у = x6 - четные функции, а у = х3, у = х5, у = х7 - нечетные функции. Если функция у = f (х) такова, что хотя бы для од ной пары значений х и -х оказалось, что f (-х) ≠ f (х) , и хотя бы для другой пары значений х и - х оказалось, что f (- х) = f (х), то функция не является ни четной, ни нечетной. Из
определения следует, что область
определения X как четной, так и нечетной
функции должна обладать следующим
свойством: если х График четной функции. График нечетной функции. Графики четной и нечетной функций обладают следующими особенностями: Если функция является четной, то ее график симметричен относительно оси ординат.
Если функция является нечетной, то ее график симметричен относительно начала координат.
G
|



