Ответ№12
Определение производной. Геометрический смысл.
Пусть функция y = f(x) определена на некотором интервале (a, b). Зафиксируем x (a, b).
(здесь рисунок)
Дадим аргументу х приращение х. Функция y = f(x) получит приращение у = f(x + х) - f(x). Отметим, что при фиксированной точке х у является функцией только x. Составим отношение:
=
-
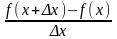функция аргумента х.
Определение:
Если существует
,
то он называется производной функции
y
= f(x)
в точке х
и обозначается f
'(x).
Другие обозначения: y'(x),
(x),
.
Примеры:
1)
y
= c
= const.
у
= f(x
+ х)
- f(x)
= с
- с
= 0,
= 0
= 0. Итак, c'
= 0.
2)
y
= xn
(n
N).
у
= (x
+ х)n
- xn
= xn
+ nxn-1х
+
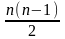xn-2(х)2
+ … + (х)n
- xn
.
= nxn-1х + xn-2(х) + … + (х)n-1, = nxn-1. Итак, (xn)' = nxn-1 (n - натуральное число).
3)
y=sin
x.
=
=
=
=
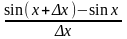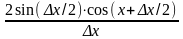cos
.
1 при х
0 (первый замечательный предел), cos
cos
x
при х
0, так как cos
x
- непрерывная функция, поэтому
=
cos
x.
Итак, (sin
x)'
= cos
x.
Геометрический смысл производной.
(здесь рисунок)
Углом
между прямой l
и осью х
назовём угол ,
на который нужно повернуть ось х
для того, чтобы совместить её положительное
направление с одним из направлений на
прямой, причём -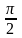
<
.
Поворот по часовой стрелке:
> 0, иначе
< 0. Число k
= tg
называется угловым коэффициентом
прямой.
(здесь рисунок)
Пусть задана функция y= f(x). Рассмотрим в прямоугольной системе координат (x, y) множество точек {(x, f(x))}, x X - области определения f(x).
(здесь рисунок)
Это множество точек представляет собой график функции y= f(x). Проведём прямую MN. Её угол с осью х обозначим (х)). Прямая MN называется секущей.
Определение. Если существует (х) = 0, то прямая l, проходящая через точку M(x, f(x)) и имеющая угловой коэффициент k = tg 0, называется касательной к графику функции y = f(x) в точке M.
Если существует (х) = 0, то прямая l называется предельным положением секущей MN при стремлении точки M к точке N по графику функции. Поэтому говорят так: касательная к графику функции в точке М - это предельное положение секущей MN.
Докажем, что если функция y = f(x) имеет производную f '(x) в точке х, то в точке M(x, f(x)) существует касательная к графику функции и угловой коэффициент касательной k = f '(x).
Доказательство:
tg (x) = , откуда (x) = arctg , (x) = arctg = [так как arctg-непрерывная функция] = = arctg( ) = arctg f '(x), так как по условию = f'(x). Существование предела (x) при x 0 и означает по определению, что в точке M (x, f(x)) существует касательная к графику функции. При этом 0 = (x) = arctg f '(x), поэтому k = tg 0 = f '(x). В этом и состоит геометрический смысл производной. Уравнение касательной к графику функции в точке M(x0, f(x0)): y - f(x0) = f '(x0)(x - x0).