Орграфы. Основные понятия.
Ор.графом наз. пара множеств, элементы 1-го множества наз. вершинами, элементы 2-го множества наз. дугами. Мн-во дуг – некоторое мн-во упорядоченных пар вершин: это озн. , что (i,j) и (j,i) различные дуги.
Понятие смежности, инцидентности, степени вершины определяется так же как и соответсвующие понятия у графа.
Дуги вида (i,j),(j,i) наз. паралельными. Ор.граф наз. простым, если он не имеет паралельных дуг. Число дуг, входящих в вершину наз. полустепенью захода d- (i).
Число дуг,
выходящих из вершины наз. полустепенью
исхода d +(i).
,где
n-число дуг. При таком сумми-ровании
каждая дуга учитывает-ся n раз. Граф
D=(N,W) лежит в основе графа G=(N,U), если он
имеет то же мн-во вершин и лю-бые две
вершины в D смежны тогда и только тогда,
когда они смежны в графе D.
Последовательность вершин ор.графа наз. маршрутом, если для любых двух соседних вершин в этой последовательности в ор.графе существует дуга (Ip,Ip+n) принадлежит U. Маршрут замкнут, если первая и последняя вершины совпадают. В противном случае – открытый.Последовательность вершин, где любые две соседние смежные наз. полумаршрутом. Маршрут, у которого все дуги различны наз. путем. Полумаршрут, у которого все дуги различны наз. полупутем. Замкнутый путь наз. контуром. Замкнутый полупуть наз. полу-контуром. Контур (полуконтур) наз. простым, если все вершины в этом контуре за исключением 1-го и последнего различны. (Аналогично для пути и полупути).
Типы связности ор.графа. Ор.граф наз. двусторонне связным, если для любой пары вер-шин(i,j) в ор.графе существует маршрут из i в j и из j в i. Ор. граф наз.односторонне связным, если для любой пары вершин(i,j) существует маршрут, соединяющий эти вершины(хоть 1). Ор. граф наз. слабосвязным,если ле-жащий в его основе граф связен или же, когда для любой пары вершин сущ. Полумаршрут, сое-диняющий эти вершины. Если граф сильно связен,то он слабо-связен и односторонне.Если он односторонне связан, то он и слабосвязен. Граф наз. не связным, если он даже не слабосвязен.
Маршруты. Цепи. Циклы. Связность.
Последовательность вершин графа G такая, что любые две соседние вершины в ней смежны, наз. маршрутом.Первая и последняя вершины – концевые. Маршрут, у к-го первая и последняя вершины совпадают наз. замкнутым, в противном случае – открытым. Маршрут, у к-го все рёбра различны наз. цепью. Замкнутая цепь – цикл. Цепь у к-й все вершины различны, наз. простой. Цикл, у к-го все вершины кроме первой и последней различны –простой. Граф наз. связным, если из любой его вершины можно попасть в любую по некоторому маршруту. Максимальный по включению связный подграф графа G наз. компонентой связности.
Способы задания графов
1.Списком рёбер
2
.Матрицей
смежности
gij= 1(i,j)ЄU
0, в противном случае
3.Матрица инцидентности
(Рёбра нумеруються, строки соответствуют номерам рёбер)
g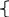
ij=
1, вершина i
и ребро j
инцидентно графе
0, в противном случае
Алгоритм распознования связности графа.
Пусть граф задан матрицей смежности. Необходимо выяснить, является ли он связным.G=(N,U), M-рабочее мн-во.
1.M=. Выбираем произвольную вершину графа i и заносим её в M.
2.Если мощность мн-ва =n(│M│=n), n-колич вершин, то граф связан и конец работы алгоритма. В противном случае переходим к третьему шагу.
3.Выбираем все такие вершины, которые не вошли в M и каждая из которых смежна по крайней мере одной вершине из M.
4.Полагаем, что все такие вершины образуют множество Р.
5.Если Р= Ø, то граф не связан. Конец работы аьгоритма и тогда G(M)-компонент связности данного графа, иначе переходим на шаг 6.
6.Расширяем множество М(M∪P) и переходим на шаг 2.
Конец алгоритма.
Алгоритм не зависит от структуры. Эффективность работы алгоритма определяется двумя параметрами:
Объём памяти, необходимый для его реализации
Время работы алгоритма.
В этой паре доминирует время.
Оценим временную сложность алгоритма распознования связности, выбрав в качестве размерности число вершин n.
Величина d имеет порядок О(f(n)) если найдётся некоторая константа с, которая не зависит от n. Такая, что d≤c·f(n)
Алгоритм распознования связности состоит из повторяющихся щагов, на каждом из которых определяется мн-ство Р и разширяется мн-ство М. Число таких шагов не превышает числа вершин графа.
Оценим временную сложность каждого такого шага.
Для построения мн-ства Р достаточно перебрать все пары вершин (і,j) іЄМ, jЄN, число таких пар не превышает n^2. Определения множества Р-самая трудоёмкая часть каждого шага. Поэтому временная сложность шага не превышает n^3. Алгоритм считается эффективным, если его временная сложность оценивается многочленом от размерности задачи.В противном случае алгоритм назыв экспонициальным. Алгоритмы, временная сложность которых оценивается полиномом от размерности задачи, называется полиномиальным. Задачи, для которыз сущ полиномиальные алгоритмы, называются хорошими, а для которых не существует-труднорешаемые.
Распознование связности-хорошая задача.