ek-ka1
.docx1.Предмет эконометрики. Измерения в экономике. Типы шкал Эконометрика — это наука, кот-аядаетколич-ое выражение взаимосвязей эконом-их явлений и процессов. Эта наука явл. своеобразным сплавом трех компонент: эконом-ой теории, статистических и матем-их методов. Становление и развитие эконометрического метода происходили на основе высшей статистики — на методах парной и множественной регрессии, парной, частной и множественной корреляции, выделении тренда и других компо-нент временного ряда, на статистическом оценивании. Признаками измерения называют получение, сравнение и упорядочение информации.В широком смысле измерение предполагает выделение некоторогосв-ва(исследование по наличию или отсутствию св-ва). Другое понимание измерения исходит из числового выражения результата, т.е. предполагает сравнение объектов по интенсивности проявляемых свойств. Третий подход к понятию измерение связан с обязательным наличием единицы измерения (эталона),( сравнение объектов с эталоном). Все понятия измерения могут быть объединены на базе определения шкалы измерения. Для определения любой шкалы измерения обязательно необходимо дать название объекта, отождествить объект с некоторым свойством или группой свойств (предприятие промышленное, станок токарный, девушка сероглазая, автомобиль легковой и т.д.). Если это требование – единственное, то шкала называется шкалой наименований или номинальной шкалой. Номинальная шкала обладает только свойствами симметричности и транзитивности. Шкала, в кот.порядок элементов по уровню проявления некоторого св-ва существенен, а количественное выражение различия несущественно наз. порядковой или ранговой. Шкала порядка допускает операции «равенство-неравенство», «больше-меньше»(рейтинг того или иного кандидата,оценка силы землетрясений).
|
2.Аддитивность и линейность связей в функции Ф-ияy=f(x1,…,xk) линейна по xi∂y/∂xiне включаетxi, т.е. ∂(∂y/∂xi) = 0. Это значит,что эффект от изменения по xiне зависит от конкретного значения xi. Функция y= f(x1,…,xk) является аддитивной по всем независимым переменным для любого i dy/dxiне включаетxj(j≠ i) т.е. ∂(∂y/∂xi)/∂xj= 0. Это значит, что эффект от изменения по каждой независимой переменной не зависит от уровня другой переменной. В этом случае совместный эффект изменения по всем учтенным независимым переменным м/б получен сложением отдельно вычисленных эффектов изменений по каждой из них. Примеры оценки линейности и аддитивности функций:
|
3.Типы данных. Выбор вида функции парной регрессия Типы данных: 1. пространственные данные – характерна независим.получ.реализацийэкономич.велечин от времени либо данные снимаются в один и тот же момент.2. временные ряды – отображают изменение эконом.пар-ров от времен.3. панельные данные – представляют собой мн-во наблюдений за однотипными объектами.Панельные данные объединяют в себе как пространст.данные,так и временные ряды. Подбор линии регрессии: Пусть для n однородных объектов сняты некоторые значения xiyi (i=1,…,n) между кот.возможносущ.связь. Можно рассм. Два варианта.1-ый–перемен.считаютсяравноценными.Основным при этом явл.вопрос о наличии и силе взаимосвязи между этими перемен.Оценкой подобного заимодействия занимается раздел – корреляционный анализ.2-ой вариант–предпологает выделение зависимой(объясняемой) и независимой(объясняющей) перемен. Объясняемая–результативный признак,объясняющие–признаки-факторы или регрессоры. Раздел,в задачу кот. Входит оценка того как объяс-щиепер-ые влияют на среднее знач.объясняемойназ.регрессоинным анализом.
Простая
или парная регрессия представляет
собой регрессию между двумя переменными
- у и х. Т.е. модель вида
Множественная регрессия соответственно представляет собой регрессию результативного признака от двух или более факторов, т.е. модель вида = f ( x 1, x2, …, xп). Реальные данные могут не укладываться в точную функцион.зависимостьт.к.на результат могут влиять другие неучтенные параметры т.е в общем случае = y+ε,где –теоретич., ε–случ.вел-на,характериз.влияние неучтенных факторов.(наз.ошибкой или возмушением).
|
4.Смысл и оценка параметров линейной регрессии. Метод наименьших квадратов
Пусть случ.вел-ныX
и Y
отображают какие-либо
экономич.параметры.Произведемn
наблюдений и получим выборку xt
,yt
(t=1,…,n).
Рассмотрим задачу «наилучшей»
аппроксимации набора наблюдений xt
,ytлинейной
функцией f(
x)
= a + bx(т.е.подбораa
и b)
в смысле
минимизации функционала: F=
Запишем условие экстремума: ∂F/∂a= 0 и ∂F/∂b= 0
Замеч.
1.
Из уравнения (4) следует,что Замеч. 2. Предполагается, что среди xt, t =1,…, n, не все числа одинаковые, т.е. var(x) ≠ 0 и (3) имеет смысл. Параметр b называют коэффициентом регрессии. Его величина показывает среднее изменение результата при изменении фактора на одну единицу. Т.е. коэффициент регрессии имеет четкую экономическую интерпретацию. Формально а - значение упри х = 0. Если же фактор х по своей природе не может иметь нулевого значения, то такая трактовка не имеет смысла.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
5.
5
Обозначим
через
Из геометрических
соображений ясно, что решением будет
та же прямая на
плоскости
|
6.. Геометрическая интерпретация МНК. Матричная форма записи МНК.
Пусть
заданы
В
пр-ве
построим вектора
Предположим,что
не колинеарны.
Поставим задачу найти такие
|
7
Кроме
оценки корреляционной зависимости
можно оценить тесноту связи между
экон. переменными. Для линейной
регрессии
является
линейный
коэффициент корреляции
Сравнивая между
собой коэффициентом
регрессии
и
Замечание. Величина линейного коэффициента корреляции оценивает тесноту связи рассматриваемых признаков в ее линейной форме. Поэтому близость его к нулю не означает отсутствие связи между признаками, Возможна связь, даже очень тесная, но не линейная.
Коэффициент
детерминации -доля
дисперсии результативного признака
Пусть по данным
|
8.
Когда найдено уравнение линейной
регрессии, проводится оценка значимости
как ур- ия в целом, так и отдельных его
пар-ров. Оценка
регрессии в целом проводится с помощью
F-критерия
Фишера:
выдвигается гипотеза
Для
анализа по F-критерия
предвор. провод. анализ дисперсии.
Вариацией СВ наз. сумму квадратов
отклонений от среднего.Рассм. разложение
сумму квадратов отклон.
Условно
разделим всю совокупность причин на
две группы: влияние
фактора
и прочие факторы. Если
фактор не оказывает влияния на
результат, то линия регрессии
на графике параллельна оси ох
и
На практике имеет место разброс как обусловленный влиянием фактора , так и вызванный действием прочих причин. Пригодность линии прогноза зависит от того, какая часть общей вариации приходится на объясненную вариацию. Любая сумма квадратов отклонений связана с числом степеней свободы (df), т.е. с кол-вом независимого варьирования признака. Число степеней свободы связано с числом единиц совокупности п и с числом определяемых по ней констант, т.е. показыв. сколько независимых отклонений из п возможных требуется для образования данной суммы квадратов. Так, для общей суммы квадратов требуется (п 1) независимых отклонений, т.к. при фиксир. по совокупности из п единиц можно варьировать (п 1) число отклонений.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
- |
Вид ф-иирегресси наз. спецификацией модели.Ошибки в спецификации относят к неправил.выбран.ф-ии и недоучтен.существенныхфакторов.От правильно выбранной спецификации модели зависит величина случайных ошибок: они тем меньше, чем в большей мере теоретические значения результативного признака подходят к фактическим данным у. Рассмотрим способы минимизации ошибок спецификации модели: 1.графическим(строится корреляционное поле и по его виду делается предположение о форме линии корреляци); 2.аналитическим, т.е. исходя из теории изучаемой взаимосвязи; 3.экспериментальным. Наиболее нагляден графический методподбора вида регрессии. Термин наилучш.линия регрессии означает подбор неизвест.пар-ов заданной специфик.регресси по к-л критерию.В качестве критерия выбора использ.минимизац.некоймеры,задающ.степень отклонения. В качестве меры отклонения можно взять следующие функционалы:
1) Сумму
квадратов отклонений F=
2) Сумму
модулей отклонений F=
3) В
общем случае F=
Примером последнего подхода является функция Хубера, которая при малых отклонения квадратичная, а при больших линейна:
|
|
Интервальные шкалы, позволяют сравнивать колич-ое отображение св-в объектов и разности этих количеств. Т.о. можно не только указать категорию, к кот.относится объект по данному признаку, установить его место в ранжированном ряде, но и описать его отличие от других объектов, рассчитав разность (интервал) между соответствующими позициями на шкале. (измерение себестоимости, рентабельности, ликвидности и т. д.). Формально интервальная шкала определяется как единственная до линейного преобразования шкала вида: у = ах + b, где а и b — числа, для которых определены операции сложения и умножения, соответственноа >0, b≠ 0. Параметра называется масштабом, а параметр b — началом отсчета. В случаях, когда на шкале можно указать абсолютный нуль, то получаем шкалу отношений (или пропорциональную шкалу). Нач.отссчета не выбирают(b=0). По шкале отношений можно оценить стаж, заработная плата.( у = ах при а ≠ 0). Если в интервальной шкале масштаб зафиксирован, то измерение происходит в шкале разностей (у = х + b, где b≠ 0-сдвиг). (указание года рождения — это представление возраста в шкале разностей.) Если зафиксированы масштаб и точка отсчета, то переменная изменяется в абсолютной шкале с точностью до тождественного преобразования вида: у = х. Точность измерения — это его адекватность. Универсальные критерии точности отсутствуют. Критерии точности каждого вида измерения определяется в соответствии с целями этого измерения.По объективным причинам для социально-экономических измерений ха-рактерна низкая контролируемость их точности. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
При расчете
объясненной(факторной) вариации
Сущ-ет соотнош.
между числом степеней свободы общей,
факторной и остаточной суммами
квадратов:
Поделив каждую
сумму квадратов отклонений на
соответствующее ей число степеней
свободы, получим среднюю
вариацию,
т.е. дисперсию
на одну степень свободы:
Если гипотеза
справедлива, то статистика F
имеет распред. Фишера со степенями
свободы 1 и
Величина F-критерия
связана с коэффициентом детерминации.
Факторную сумму квадратов отклонений
можно представить как
|
Разделив (5) на
левую часть, получим:
Поделив числитель
и знаменатель каждой дроби (6) на
,
в левой
части получим долю дисперсии
результативного признака
,
объясняемую
регрессией, в общей дисперсии
результативного признака.:
Величина
Связь
между
и
и линейный
коэффициент детерминации
|
Получаем
Сравнивая
полученный результат с (
и
Матричная форма записи МНК Введем
матрицу
Замечание: Матрица не вырождена,т.к. матр. имеет максимал. rang=2
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
9.Природа ошибок регрессии. Основные гипотезы для обоснования парной линейной регрессионной модели Линейная регрессионная модель обосновывается корректно, если выполн. след.условия:
1.
спец-кация модели:
2.
– детерменир-наявел-на (неслучайная),
причём вектор
3а.
4.
Эти условия являются основными. Для оценки некоторых интервальных хар-к используется ещё одно:
5.
Ошибки
В этом случае модель называется классич. нормал. лин. регрессионной.
Зам.
При выполнении усл. 5 усл-вие 4°
эквивалентно условию статистической
независимости ошибок
Реальные модели не «обязаны» соблюдать эти условия. Рассмотрим условия 1° – 4° и их возможные нарушения: >Усл. 1° указывает на спец-цию модели как парной линейной регрессии. Возможно, что на результативный признак оказывает значимое влияние не одна, а несколько независимых переменных (множеств.регрессии) или влияние имеет нелин. вид (нелин. регрессия). >Усл. 2° означает, что не все регрессоры одинаковы. При невыполнении этого условия регрессионную модель построить невозможно.
>Усл.
3a° означ., что
>Усл. 3б° говорит о независимости дисперсии ошибки от номера наблюдения и называется гомоскедастичностью; противоположный случай называется гетероскедастичностью
|
10. Теорема Гаусса-Маркова для парной линейной регрессии Пусть имеется набор данных (Xt, Yt), t =1,…, n, задав-ых при выполн. усл-ий:
1.
– спец-кация модели. 2.
– детерменир-ная вел-на, причём вектор
не коллинеар. вектору
Необход.
оценить «наилуч.» способом все 3
параметра a, b и
Зам.Если такая оценка найдена, то это не означает, что не сущ. нелин. оценки с меньшей дисперсией, или минимум дисперсии оценки можно получить, если отбросить требования несмещ.
Теор.
Гаусса-Маркова.
В предположении модели с условиями
1– 4 оценки
Док-во.
1.
Проверка,
являются несмещ. оценками истинных
знач. a и b:
2.
Нахождение
Представим
Представим
в виде:
|
11. Оценка дисперсии ошибок . Дисперсия ошибок также является пар-ром регрессии.
Обозн. через
Предположим, что оценка связана с суммой квадратов остатков регрессии.
Найдём математическое
ожидание полученной суммы:
Используя
Таким образом:
|
12. Оценка существенности параметров линейной регрессии и корреляции.
В
линейной регрессии
При выполнении дополнительного условия о совместном нормальном распределении ошибок, стандартная ошибка коэффициента регрессии параметра рассчит-ся по формуле:
Отношение
коэффициента регрессии к его стандартной
ошибке даёт t-статистику (
Для
проверки значимости коэф-та регрессии
вычесл. зна-ние
Рассматривается
2 гипотезы:
Опр. Ошибкой 1 рода наз. отклонение основ.гип. , если она была истинна.
По
таблицам критических значений получают
критическую точку. Если
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
13.Интервалы прогноза по линейному уравнению регрессии
Основное
назначение уравнения регрессии —
прогноз возможных значений результата
при заданном значении фактора. Этот
прогноз осуществляется путем
подстановки значения фактора Х =
это
выражение в уравнение
.
=
Величина
стандартной ошибки предсказания
зависит от
,
достигает минимума при
= X и возрастает по мере того, как
«удаляется» от X в любом направлении.
Для прогнози-руемого значения
95%-ные доверительные интервалы при
заданном
определяются выражением
|
14. Нелинейная регрессия. Линеаризируемые и нелинеаризируемые модели.эластичность Линейная регрессия является частным, и не самым распространенным случаем регрессии.
Примером
нелинейнойрегресииявл.: 1)
Различают два класса нелинейных регрессий. 1. Регрессии нелинейные относительнообъясняющих переменных (факторов), но линейные по оцениваемым параметрам; 2. Регрессии нелинейные по оцениваемым параметрам. Оценка неизвестных параметров нелинейных регрессий первого класса решаются безсложностей методом наименьших квадратов. Возможны и иные модели, нелинейные по фактору, но линейные по неизвестным параметрам. Все случаи регрессий нелинейных по оцениваемым параметрам делятся на 2 типа: внутренне линейные и внутренне нелинейные модели. Внутренне линейная модель с помощью математических преобразований может быть сведена к линейному виду. Если же модель внутренне нелинейна, то она не может быть сведена к линейной модели. |
15.Корреляция
для нелинейной регрессии. Средняя
ошибка аппроксимации
Уравнение
нелинейной регрессии, так же как и в
линейной зависимости, дополняется
показателем корреляции, а именно
индексом корреляции R:
Иначе
обстоит дело, когда преобразования
уравнения в линейную форму связаны
с зависимойпер-ной. В этом случае
лин.коэф. корреляции по преобразованным
знач. признаков дает лишь приближенную
оценку тесноты связи и численно не
совпадает с индексом корреляции.Поскольку
в расчете индекса корреляции исп-ся
соотношение факторной и общей суммы
квадратов отклонений, то
Вел-на т хар. число степеней свободы для факт.суммы квадратов, а (n–m–1) — число степеней свободы для остат. суммы квадратов. |
16.Множественная регрессия. Спецификация модели. Отбор факторов
Парная
регрессия испол. в случае, когда на
результативный признак оказывает
сущ-ное влияние 1 фактор, а все прочие
факторы явл.несущ-ыми и входят в ошибку
измерения. Если нельзя искл. несколько
факторов как сущ., то получаем случай
множ. регрессии. Общий вид: Построение ур-ниямнож. регрессии начинается с решения вопроса о спец-ции модели. Она включает в себя два круга вопросов: отбор факторов и выбор вида ур-ния регрессии.Включение в ур-ниемнож. регрессии того или иного набора факторов связано, прежде всего, с представлением исследователя о природе взаимосвязи моделируемого пок-ля с другими эк. явлениями. Факторы, включа. во множ. регрессию, должны отвечать след.требованиям. 1. Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность 2. Факторы не должны быть интеркоррелированы и тем более находиться в точной функциональной связи.
Включение
в модель факторов с высокой
интеркорреляцией, когда
Включаемые во множественную регрессию факторы Должны объяснить вариацию независимой переменной. Если строится модель с набором р факторов, то для нее рассчитывается показатель детерминации , который фиксирует долю объясненной вариации результативного признака за счет рассматриваемых в регрессии р факторов. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Рассм.
Св-ва величины
Стандартная
ошибка параметра а определяется по
формуле:
Значимость
линейного коэффициента корреляции
проверяется на основе величины ошибки
коэф-та корреляции
Т.о.
Учитывая,
что
|
Зам. 1.
Предпол., что мы изучаем зависимость
Y от
Х и
число наблюдений n
задано
Зам. 2.
На практике, как правило, дисперсия
ошибок
неизвестна
и оценивается по наблюдениям
одновременно с коэффициентами
регрессии а
иb.
Поэтому вместо дисперсий оценок
можем получить оценки дисперсий
заменив
на
Станд. Отклон.
оценок этих параметров (использ.В
стат. Пакетах) вычисл. на основе этих
формул, например
|
Тогда
Найдём
ковариацию:
Зам.
Из
формулы (1) след., что
3. Покажем, что МНК-оценки явл. «наилучш.» в классе всех лин. несмещ. оценок.
Пусть
|
>Усл. 4° указывает на некоррелированность ошибок для разных наблюдений, т.е. величина одной ошибки не влияет на другую. Это условие часто нарушается, особенно если данные являются временными рядами.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Влияние
других не учтенных в модели факторов
оценивается как 1 –
с соответствующей остаточной дисперсией
.
При дополнительном включении в
регрессию р
+ 1
фактора коэффициент детерминации
должен возрастать, а остаточная
дисперсия уменьшаться:
Насыщение модели лишними факторами не только не снижает величину остаточной дисперсии и не увеличивает показатель детерминации, но и приводит к статистической незначимости параметров регрессии по t-критерию Стьюдента. Хотя теоретически регрессионная модель позволяет учесть любое число факторов, практически в этом нет необходимости. Отбор факторов производится на основе качественного теоретико-экономического анализа. Однако теоретический анализ часто не позволяет однозначно ответить на вопрос о количественной взаимосвязи рассматриваемых признаков и целесообразности включения фактора в модель. Поэтому отбор факторов обычно осуществляется в две стадии: на первой подбираются факторы исходя из сущности проблемы; на второй — на основе матрицы показателей корреляции определяют t-статистики для параметров регрессии.
Коэффициенты
интеркорреляции (т.е. корреляции между
объясняющими переменными) позволяют
исключать из модели дублирующие
факторы. Считается, что две переменных
явно коллинеарны, т. е. находятся между
собой в линейной зависимости, если
|
Индекс
дет.
Факт-кие
знач.Резул-ного признака отличаются
от теор-ких, рассчитанных по ур-нию
регрессии, т. е.
|
Особый
интерес среди нелинейных функций
регрессии представляет степенная
функция
В
общем случае, коэффициент эластичности
может быть определен для любой функции
регрессии
|
На
графике доверительные границы для
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
17.МНК для множественной регрессии. Мультиколлинеарностьее последствия. Рассмотрим линейную модель множественной регрессии:
Классический подход к оцениванию параметров линейной модели множественной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака от расчетных минимальна:
Вычислим частные производные первого порядка по каждому из параметров и приравняем их к нулю.Имеем функцию аргумента:
Находим частные производные первого порядка:
После элементарных преобразований приходим к системе линейных нормальных уравнений для нахождения параметров линейного уравнения множественной регрессии:
|
18.Множественная регрессия в стандартизованном масштабе. Возможен подход к определению параметров множ. регрессии. Строится регрессия в стандартизированном масштабе.
где
Применяя МНК к уравнению в стандартизированном масштабе получим после преобразований систему уравнений вида
Решая
еенайдем параметры
В
парной регрессии стандартизированный
коэффициент регрессии это линейный
коэффициент корреляции
.
Поэтому, можно получить
формулу связи чистой регрессии
|
19. Множественная корреляция. Скорректированный индекс детерминации. Введем показатель множ. корреляции и его квадрата - коэффициента детерминации. Показатель множ. корреляции характеризует тесноту связи рассм-мого набора факторов с исследуемым признаком. Независимо от формы связи в кач-вепок-ля множ. корреляции может быть использован индекс множ. корреляции
Величина индекса множественной корреляции должна быть не меньше максимального индекса парной корреляции. При правильном включении дополнительных факторов в регрессионную модель величина индекса множественной корреляции должен существенно отличаться от индексов парной корреляции. Если же эти индексы практически совпадают, то это значит что вновь включаемые факторы - незначительны. При линейной зависимости признаков формула индекса множественной корреляции может быть представлена выражением
где
Формула индекса множественной корреляции (1) для линейной регрессии получила название лин. коэффициента множественной корреляции, или совокупного коэффициента корреляции. Возможно также при линейной зависимости определение совокупного коэффициента корреляции через матрицу парных коэффициентов корреляции:
где
|
24. Гетероскедастичность и ее последствия. Тесты на гетероскедастичность. Метод взвешенных наименьших квадратов Рассмотрим проблемы, возник.при нарушениях третьей гипотезы, о незав-ти дисперсии ошибок от значения регрессора и о некор-ности ошибок регрессии между собой. Нарушение первого из этих принципов называют гетероскедастичностью, а второго автокорреляцией ошибок. Наличие гетероскед. может в отдельных случаях привести к смещ. оценок коэф-тов регрессии, хотя несмещ. оценок коэффициентов регрессии в основном зависит от соблюдения 2 предпосылки МНК, т.е. независ. остатков и величин факторов. Гетероскед. будет сказываться на уменьш.эф-сти оценок bi. В част-ности, становится затруднительным испол-ние формулы станд. ошибки коэф-та регрессии Sb, предполаг. единую дисперсию остатков для любых значений фактора. С этой целью рекомендуется испол. обобщенныйМНК, который эквивалентен обыкн.МНК, примен. к преобраз-ным данным. Чтобы убедиться в необходимости испол-нияобобщ. МНК, обычно не ограничиваются визуальной проверкой гетероскед-ти, а проводят еёэмпир. подтверждение. При малом объеме выборки, что наиболее характерно для эконометрич. исследований, для оценки гетер-сти может испол. метод Гольдфельда – Квандта. Гольдфельд и Квандт рассмотрели однофакторную лин. модель, для кот.дисперсия остатков возрастает пропорц-но квадрату фактора. Чтобы оценить нарушение гомоскедастичности, они предложили параметрический теcт, кот.включает в себя следующие шаги: 1) Упорядочение п наблюдений по мере возрастания переменной х.2) Исключение из рассмотренияСцентральных наблюдений; при этом (п– С)/2 >р, где р — число оцениваемых параметров. 3) Разделение совокупности из (п – С) наблюдений на две группы (соотв-но с малыми и большими значениями фактора х) и определение по каждой из групп уравнений регрессии. 4)Определ. остаточной суммы квадратов для первой (S1) и второй (S2) групп и нахождение их отношения: R= S1/ S2 При выполнении нулевой гипотезы о гомоскедастичности отношение Rбудет удовлетворять F-критерию с (п-С-2р) / 2 степенями свободы для каждой остаточной суммы квадратов. Чем больше величина Rпревышает табл. значение F-критерия тем более нарушена предпосылка о рав-ве дисперсий остат. величин. При нарушении гомоскед. и наличии автокорреляции ошибок реком.традиц.МНК заменять обобщеннымМНК. Обобщ.МНКпримен. к преобраз. данным и позволяет получать оценки, которые обладают не только св-вомнесмещ., но и имеют меньшие выборочные дисперсии. Рассмотрим использование обобщ. МНК для корректировки гетер-ти. Предположим, что ср. значение остаточных величин равно 0,а дисперсия их не остаётся неизменной для разныхзнач. фактора, а пропорциональна величине Кt, т.е.
где
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
21.Оценка надёжности результатов множественной регрессии и корреляции. Частный F-критерий
Значимость
уравнения множественной регрессии
в целом, также как и в парной
регрессии, оценивается с помощью
F-критерия Фишера:
Оценивается знач-ть не только уравнения в целом, но и фактора, дополнительно включ. в регрес-ную модель. Необходимость такой оценки связана с тем, что не каждый фактор, вошедший в модель, может существенно увелич. долю объяснённой вариации резул-ного признака. Кроме того, при наличии в модели нескольких факторов они могут вводиться в модель в разной последов-ти. Ввиду корреляции между факторами значимость одного и того же фактора может быть разной в зависимости от последовательности его введения в модель. Мерой для оценки включения фактора в модель служит частный F-критерий.
Частный
F-критерий построен на сравнении
прироста факторной дисперсии,
обусловленного влиянием доп. включённого
фактора, с остаточной дисперсией на
одну степень свободы по регрессионной
модели в целом. Если оцениваем
значимость влияния фактора xiкак
дополнительно включенного в модель
фактора, то используем следующую
формулу:
В
числителе формулы показан прирост
доли объяснённой вариации узасчет
дополнительноговключения в модель
соответствующего фактора xi.В
знаменателе доля остаточной вариации
по регрессионной модели,включающей
полный набор факторов. Если числитель
и знаменатель Fxумножить
на
|
22. Фиктивные переменные Обычно факторы в регрессионной модели имеют непрерывные области изменения (нац. доход). Но часто некоторые регрессоры могут принимать только два значения или в общем случае дискретноемн-во значений. Например, исследуя зависимость зарплаты от различных факторов возникает вопрос, влияет ли на ее размер наличие у работника высшего образования или его пол. Можно оценивать соответствующие уравнения внутри каждой категории, а затем изучать различия между ними. Но введение дискретных переменных позволяет оценивать одно уравнение сразу по всем категориям. Рассмотрим пример с зарплатой. Пусть xt=(xt1,…,xtk)ˊ - набор объясняющих переменных, т.е. первоначальная модель описывается уравнениямиyt = xt1β1+…+ xtkβk + εt = x'tβ + εt,t = 1,…, n ,где yt - размер зарплаты t-го работника. Теперь мы хотим включить в рассм-ние такой фактор, как наличие (отсутствие)высшегообр-ния. Введём новую бинарную переменную d, полагая dt = 1, если в t-ом наблюдении субъект имеет высш.образ. и dt = 0 в противном случае, рассмотрим новую систему yt = xt1β1+…+ xtkβk + dtδ + εt = z'tγ + εt,t = 1,…,n, где z = (xt1,…, xtk, dt)', γ = (β1,… , βk , δ)'. С точки зрения этой модели средняя зарплата есть x'tβ + δ - при наличии высшего образования и x'tβ - при его отсутствии. Т.о., величинаδинтерпр. как среднее изменение зарплаты при переходе из одной категории (без высш. образ.) в другую (с высш.образ.) при неизменных значениях других пар-ов. Применяя к системе МНК получаем оценки соответствующихкоэф-тов. Такиеперем.наз. фиктивными, однако это такая же «равноправная» перем., как и любой из регрессоров. Ее «фиктивность» состоит только в том, что она колич. описываеткач. признак. Качеств.различие можно формал-ть с помощью любой переменной,приним. два разл. значения не обязательно 0 и 1. Но всоврем.эконометрике почти всегдаиспол.фикт.перем. со знач. 0 и 1, т.к. в этомслучае интерп-ция выглядит наиболее просто.
|
23. Оценка максимального правдоподобия коэффициентов регрессии Наряду с МНК возможен и другой подход к оцениванию параметров линейного регрес. уравнения по данным наблюдений - метод максим.правдоподобия. Рассмотрим его применение к оцениванию параметров парной регрессии. Предп., что мы ищем параметры нормальной линейной регрессионной моделиyt = a + bxt + εt Ошибки регрессии εt независимы и распределены по нормальному закону: εt ~ N(0,σ2), или, что является эквивалентной записью Y ~ N(a + bX, σ2). Имея набор наблюдений (xt ,yt), t = 1,..., n, мы можем попытаться ответить на вопрос: при каких значениях пар-ров а, b, σ2 моделивероятность получить этот набор наблюдений наибольшая? Другими словами, каковы наиболее вероятные значения параметров модели для данного набора наблюдений?
Чтобы
ответить на этот вопрос, составим
функцию
правдоподобия,
равную произведению плотностей
вероятности отдельных наблюдений:
Чтобы
найти наиболее правдоподобные значения
параметров, нам необходимо найти
такие их значения, при которых ф-ция
правдоподобия L
достигает своего максимума. Так как
ф-цииL
и lnL
одновременно достиг.своего максимума,
дост-ноискать максимум лог-ма ф-ции
правдоподобия Необходимые условия экстремума функции lnL имеют вид:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
В
общем виде для уравненияyt
= a + bxt
+ εt
при
В ней остаточные величины гетероск.
Предполагая
в них отсутствие автокорреляции,
можно перейти к ур-нию с гомоскед.
остатками, поделив все переменные
на
По
отношению к об.регрессииур-ние с
преобраз.перем.представл.
собой взвешенную
регрессию,
в
кот. перем.у
и
х
взяты
с весами
Оценка параметров нов.уравнения с преобразованными переменными приводит к взвешенному методу наименьших квадратов, для кот.необх.Миним-ть сумму квадратов отклонений вида
При
обычном прим-нииМНКкоэф. регрессии
b
определяется
по формуле При испол-нииобобщ. МНК с целью корректировки гетероскед.коэф.регрессииb представляет собой взвешенную величину по отношению к обычному МНК с весами 1/К. Аналогичный подход возможен не только для уравнения парной, но и для множ. регрессии. Предположим, что рассматривается модель вида
для
которой дисперсия остаточных величин
оказалась пропорциональна
где ошибки гетероскедастичны Чтобы получить уравнение, где остатки гомоскедастичны, перейдем к новым преобраз. переменным, разделив все члены исходного уравнения на коэффициент пропорц-тиК:
Найдя переменные в новом преобразованном виде и применяя об. МНК к ним, получим иную спецификацию модели
Параметры такой модели зависят от концепции, принятой коэффициента пропорц-тиKt. Следует иметь в виду, что новые преобразованные переменные получают новое экономическое содержание и их регрессия имеет иной смысл, чем регрессия по исходным данным.
|
Для
ур-ния Рассм-ная формула позволяет определять сов.коэффициент корреляции, не обращаясь при этом к ур-ниюмнож.регрессии, а используя лишь парные коэффициенты корреляции.
Формула
скорректированного индекса множ.
детерминации имеет вид:
Поскольку
Зам. Предложенный способ корректировки является в достаточной степени искусственным и ни откуда не вытекающим. Вел-на коэф.множ. детерминации исп-ся для оценки качества регрессионной модели. Низкое значение коэф. (индекса) множ.й корреляции может означать, что в регрес. модель не включены сущ-ные факторы - с одной стороны, а с другой стороны - рассматриваемая форма связи не отражает реальные соотношения между пер-ными, включ. в модель. Требуются дальнейшие исследования по улучш. качества модели и увелич.еепракт.знач-ти. |
Это позволяет ур-ние регрессии в стандартиз. масштабе (1) привести к уравнению регрессии в натуральном масштабе . Параметра определяется как
Рассмотренный смысл стандартизированных коэффициентов регрессии позволяет использовать их при отсеве факторов. Из модели исключаются факторы с наименьшим значением .
|
По величине парных коэффициентов корреляции обнаруживается лишь явнаяколлинеарность факторов. Наибольшие трудности в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарностифакторов, когда более чем два фактора связаны между собой линейной зависимостью, т.е. имеет место совокупное воздействие факторов друг на друга. Наличие мультиколлинеарности факторов может означать, что некоторые факторы будут всегда действовать в унисон. В результате вариация в исходных данных перестает быть полностью независимой, и нельзя оценить воздействие каждого фактора в отдельности. Чем сильнее мультиколлинеарность факторов, тем менее надежна оценка распределения суммы объясненной вариации по отдельным факторам с помощью МНК. Включение в модель мультиколлинеарных факторов нежелательно в силу следующих последствий:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Решением системы уравнений являются оценки максимального правдоподобия.
Отметим, что оценки максимального правдоподобия (ML) параметров a, b совпадают с оценками метода наименьших квадратов (OLS). Это легко видеть из того, что уравнения совпадают с соответствующими уравнениями МНК. Оценка максимального правдоподобия для σ2 не совпадает с (OLS)-оценкой σ2
котораяявл. несмещенной оценкой дисперсии ошибок.
Т.о.,
|
Если включаемый в рассмотрение кач. признак имеет не два, а несколько значений, то в принципе можно было бы ввести дискретную переменную, приним. такое же кол-во значений. Но такую модель было бы трудно содержательно интерпретировать. Обычно используют несколько бинарных переменных. Типичным примером может служить модель исследования сезонных колебаний. Пусть yt - объем потребления некоторого продукта в месяц t, и есть все основания считать, что потребление зависит от времени года. Введём три бинарные переменные d1, d2, d3: dt1 = 1, если месяц t явл.зимним, dt1 = 0 в остальных случаях; dt2 = 1, если месяц t явл.весенним, dt2 = 0 в остальных случаях; dtз = 1, если месяц t явл.летним, dt3 = 0 в остальных случаях; и оцениваем уравнение yt = β0 + dt1 β1 + dt2 β2 + dt3 β3 + εt Зам. В модель не вводится четвертая бинарная переменная d4 относящаяся к осени, т.к. иначе для любого месяца t вып. бы тождество d1 + d2 + d3 + d4 = 1, что означало бы лин. зависимость регрессоров и как следствие, невозможность получения МНК-оценок. По этом модели среднемесячногообъема потребления есть β0 для осенних месяцев, β0 + β1 - для зимних, β0 + β2 - для весенних и β0 + β3 - для летних.
|
Чтобы получить величину F-критерия, необходимо эти суммы квадратов отклонений разделить на соответствующее число степеней свободы. Т.к. прирост факторной суммы квадратов откл-ний обусловлен доп. включением в модель одного исследуемого фактора хi, то число степеней свободы для него равно 1. Для остаточной суммы квадратов отклонений по регрес. модели число степеней свободы, как уже было рассмотрено ранее, равно: п-т-1. Соотношение числа степеней свободы приведено в формуле частного F-критерия в виде дроби: (п-т-1)/1. Фактич. знач. частного F-критерия сравнивается с табл. при заданном уровне значимости и числе степеней свободы: 1 и п-т-1. Если факт.значение Fxпревышает Fкрит то доп. включение фактора хiв модель статистически оправданно и коэффициент чистой регрессии bi, при факторе хiстат. значим. В противном случае доп. включение в модель фактора хiне увеличивает существенно долю объяснённой вариации признака у, следовательно, нецелесообразно его включение в модель. С помощью частного F-критерия можно проверить значимость всех коэф. регрессии в предположении, что каждый соответствующий фактор хiвводился в уравнение множ. регрессии последним.
Оценка
значимости коэффициентов чистой
регрессии по t-критерию
Стьюдента может быть проведена и без
расчёта частных F-критериев.
В этом случае, как и в парной регрессии,
для каждого фактора используется
формула
Для
уравнения множественной регрессии Чтобы воспользоваться данной формулой, необходимы матрица межфакторной корреляции и расчет .
Так
для уравнения
Если
учесть, что
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
25.Автокорреляция в остатках. Критерий Дарбина-Уотсона (Д-У). Говорят о наличии автокорреляции остатков, если каждое текущее значение остатков зависит от предшествующих (последующих) значений (остатки содержат тенденцию или циклические колебания, а в соответствии с предпосылками МНК остатки εi, должны быть случайными). Причины автокорреляции остатков: 1) иногда автокорреляция связана с исходными данными и вызвана наличием ошибок измерения в значениях Y. 2) иногда причину автокорреляции остатков следует искать в формулировке модели. В модель может быть не включен фактор, оказывающий существенное воздействие на результат, но влияние, которого отражается в остатках, вследствие чего последние могут оказаться автокоррелированными. Зачастую этим фактором является фактор времени t. Иногда, в качестве существенных факторов могут выступать лаговые значения переменных, включенных в модель. Либо в модели не учтено несколько второстепенных факторов, совместное влияние которых на результат существенно ввиду совпадения тенденций их изменения или циклических колебаний. Методы определения автокорреляции остатков
1
метод – это постр. графика зав-ти
остатков от времени и визуальное
опред. наличия или отсутствия
автокорреляции. 2 метод — исп. критерия
Д-У и расчет величины:
Т.е. кр.Д-Уопредел. как отн-ние суммы квадратов разностей послед-ных значений остатков к сумме квадратов остатков.
Коэффициент
автокорреляции 1 порядка определяется:
Соотношение
между кр. Д-У и коэф-том автокорреляции
остатков первого порядка определяется
зависимостью:
|
26.Оценивание параметров уравнения регрессии при наличии автокорреляции в остатках
Рассмотрим
уравнение регрессии
• Пусть оц. а и b пар-ров ур-ния регрессии найдены об. МНК; • Пусть кр.Д–У показал наличие автокор. в остатках 1 порядка.
Чтобы
понять, каковы последствия автокорреляции
в остатках для оценок пар-ров модели
регрессии, найденных об. МНК, построим
формальную модель, описыв. автокорреляцию
в остатках. Автокорреляция в остатках
1 порядка предпол., что каждый
след.уровень остатков etзависит
от предыд. уровня et
–1.
Следов., сущ-ет модель регрессии вида
В
соответствии с формулами МНК имеем:
После
преобраз-ний имеем:
Т.
о.:
Текущий уровень ряда уtзависит не только от факт.перем. хt, но и от остатков предш-его периода. Допустим, мы не приним. во внимание эту информацию и опред. оценки пар-ров а и bур-ния регрессии об. МНК. Тогда получ. оценки неэффективны, т.е. они не имеют миним. дисперсию. Это приводит к увелич.станд. ошибок, снижению фактич. значений t-критерия и широким доверительным интервалам для коэффициента регрессии. На основе таких результатов можно сделать ошиб.вывод о незначимом влиянии исслед. фактора на результат, в то время как на самом деле его влияние статистически значимо.
Основной
подход к оценке параметров модели
регрессии в случае, когда имеет место
автокорреляция остатков.
Обратимся к исходной модели (1). Для
момента времени t–1
модель примет вид:
Умножим
обе части уравнения на
|
27.Системы одновременных эконометрических уравнений. Структурная и приведенная форма модели. Идентифицируемые, неидентифицируемые и сверхидентифицируемые системы. Отдельно взятое уравнение множ. регрессии не может характеризовать истинные влияния отдельных факторов на вариацию результ.пер-ной. Поэтому в эконометрике важное место заняла проблема описания структуры связей пер-ными – системой одновременных уравнений (структурными уравнениями). Структурная и приведенная формы модели (СФ и ПФ) Система совместных, одноврем. уравнений (или структ. форма модели) обычно содержит эндогенные и экзогенные переменные. Энд.пер-ные- это завис. Пер-ные (у). Число эндогенных переменных равно числу ур-ний в системе. Экз.пер-ные- это предопред.пер-ные, влияющие на энд.пер-ные, но не завис.от них (х). Простейшая структурная форма модели имеет вид:
Коэффициенты biи ai наз.структурными коэффициентами(CK). Все переменные в модели выражены в откл-ниях от средн. уровня. Поэтому своб. член в каждом ур-нии системы отсутствует. Испол-ние МНК для оценивания СКдаётсмещённые и несостоятельные оценки. Поэтому обычно для опред-нияСКCФ преобразуется в приведенную форму модели. ПФпредст. собой систему лин. ф-ций энд.пер-ных от экз.:
где
Применяя МНК, можно оценить , а затем оценить значения энд.пер-ных через экз.
ПК
представляют собой нелинейные
функции СК:
При переходе от ПФ к СФ возникает проблема идентификации. |
28. Необходимые и достаточные признаки идентифицируемости системы Модель считается идентифицируемой, если каждое уравнение системы идентифицируемо. Если хотя бы 1 уравнение системы не идентифицируемо, то и вся модель неидентифицируема. Сверхидентифицируемая модель содержит хотя бы 1 сверхидентифицируемое уравнение. Необходимое условие Чтобы 1 конкретное уравнение модели было идентифицируемо, необходимо, чтобы число предопределенных переменных (факторов) отсутствующих в данном уравнении, но присутствующих в системе, было равно числу эндогенных переменных в данном уравнении без одного. Обозначим число эндогенных переменныхв j-ом уравнении через Hj, а число экзогенных переменных содержащихся в системе, но отсутствующих в уравнении - через Dj. Тогда условие идентифицируемости записывается в виде следующего счетного правила Dj + 1 = Hj - уравнение идентифицируемо; Dj+ 1 <Hj- уравнение неидентифицируемо; Dj+ 1 >Hj- уравнение сверхидентифицируемо; Достаточное условие Уравнение идентифицируемо, если по отсутствующим в нем переменным (эндогенным и экзогенным) можно из коэффициентов при них в других уравнениях системы получить матрицу, определитель которой не равен нулю, а ранг матрицы не меньше чем число эндогенных переменных в системе без одного. Целесообразность проверки условия идентификации модели через определитель матрицы коэффициентов, отсутствующих в данном уравнении, но присутствующих в других, объясняется тем, что возможна ситуация, когда для каждого уравнения системы выполнено счетное правило, а определитель матрицы названных коэффициентов равен нулю. В этом случае соблюдается лишь необходимое, но недостаточное условие идентификации.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
20.Частная корреляция при множественной регрессии. Процедура пошагового отбора переменных Высокое значение коэффициента корреляции между исследуемой зависимой и какой-либо незав. переменной может, означать высокую степень зависимости, но может быть обусловлено другой причиной. А именно, есть третья переменная, которая оказывает сильное влияние на две первые, что и служит, в конечном счете, причиной их высокой коррелированности. Поэтому возникает естественная задача найти «чистую» корреляцию между двумя перем., исключив влияние других факторов. Это можно сделать с пом. коэффициента частной корреляции. Для простоты предположим, что имеется регрессионная модель
Наша
цель - определить корреляцию между
и,
например, первым регрессором
Соответствующая процедура устроена следующим образом.
1.
Осуществим регрессию
на
и
константу и получим прогнозные
значения
2.
Осуществим регрессию
на
и
константу и получим прогнозные
значения
3.
Удалим влияние
,
взяв
остатки
4.Определим
(выборочный) коэффициент частной
корреляции между
и
при
исключении влияния
как (выборочный) коэффициенткорреляции
между
На практике довольно часто приходится сталкиваться с ситуацией, когда имеется большое число наблюдений различных параметров (независимых переменных), но нет априорной модели изучаемого явления. Возникает естественная проблема, какие переменные включить в регрессионную схему. Процедура присоединения-удаления На первом шаге из исходного набора объясняющих переменных выбирается (включается в число регрессоров) переменная, имеющая наибольший по модулю коэффициент корреляции с зависимой переменной .
|
29. .Коэффициенты структурной модели могут быть оценены разными способами в зависимости от вида системы одновременных уравнений. Наибольшее распространение в литературе получили следующие методы оценивания коэффициентов структурной модели: • косвенный метод наименьших квадратов; • двухшаговый метод наименьших квадратов; Косвенный метод наименьших квадратов (КМНК) применяется для идентифицируемой системы одновременных уравнений, а двухшаговый метод наименьших квадратов (ДМНК) используется для оценки коэффициентов сверхидентифицируемой модели. Дальнейшим развитием ДМНК является трехшаговый МНК (ТМНК). Этот метод оценивания пригоден для всех видов уравнений структурной модели. Косвенный метод наименьших квадратов (КМНК) Как уже отмечалось, КМНК применяется в случае точно идентифицируемой структурной модели. Процедура применения КМНК предполагает выполнение следующих этапов работы. 1. Структурная модель преобразовывается в приведенную форму модели. 2.
Для каждого уравнения приведенной
формы модели обычным МНК оцениваются
приведенные коэффициенты
3. Коэффициенты приведенной формы модели трансформируются в параметры структурной модели. применение
КМНК для простейшей идентифицируемой
эконометрической модели с двумя
эндогенными и двумя экзогенными
переменными:
|
30. Двухшаговый метод наименьших квадратов (ДМНК) Как уже отмечалось, ДМНК используется для оценки параметров сверхидентифицируемой модели. Процедура применения ДМНК предполагает выполнение следующих этапов работы. 1. Модель преобразовывается в приведенную форму. 2. На основе приведенной формы получают теоретические значения эндогенных переменных, содержащихся в правой части уравнения. 3. Подставляя полученные теоретические значения эндогенные переменных вместо фактических значений, применяют обычный МНК к структурнойформе сверхидентифицируемого уравнения. Метод получил название двухшагового МНК, т.к. дважды используется МНК: первый — при определении приведенной формы модели и нахождении на ее основе оценок теоретических значений эндогенных переменных; второй — применительно к структурному сверхидентифицированному уравнению для определения структурных коэффициентов модели по экзогенным фактическим и эндогенным теоретическим (расчетным) значениям переменных. Сверхидентифицируемая структурная модель может быть двух типов: 1. все уравнения системы сверхидентифицируемы; 2. система содержит как сверхидентифицируемые, так и точно идентифицируемые уравнения. В первом случае для оценки структурных коэффициентов каждого уравнения применяется ДМНК. Во втором случае, для полностью идентифицируемых уравнений, структурные коэффициенты находятся из системы приведенных уравнений.
|
32. Одним из наиболее распространенных способов моделирования тенденции временного ряда является построение аналитической функции, характеризующей зависимость уровней ряда от времени, или тренда. Этот способ называют аналитическим выравниванием временного ряда. Поскольку зависимость от времени может принимать разные формы, для ее формализации можно использовать различные виды функций. Для построения трендов чаще всего применяются следующие функции:
линейный
тренд:
гипербола:
экспоненциальный
тренд:
тренд
в форме степенной функции
парабола второго и более высоких порядков
Параметры
каждого из перечисленных выше трендов
можно определить обычным МНК, используя
в качестве независимой переменной
время
Наиболее распространеннй способ определения типа тенденции является качественный анализ изучаемого процесса, построение и визуальный анализ графика зависимости уровней ряда от времени, расчет некоторых основных показателей динамики. В этих же целях можно использовать и коэффициенты автокорреляции уровней ряда. Тип тенденции можно определить путем сравнения коэффициентов автокорреляции первого порядка, рассчитанных по исходным и преобразованным уровням ряда. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Идентификация - это един.соот-вия между ПФ и СФ модели. Пусть структурная модель имеет вид:
Из 2 уравнения можно выразить у1 следующей формулой:
Тогда в системе имеем 2ур-ния для энд.пер-ной у1с одним и тем же набором экз.пер-ных, но c разными коэф-тамипри них:
Наличие двух вариантов для расчёта СК одной и той же модели связано с неполной еёидентиф-цией. СМ в полном виде, состоящая в каждом ур-нии системы из пэнд. и т экз. пер-ных, содержит п(п-1+т) пар-ров. ПФ модели содержит птпараметров. В полном виде СМ содержит большее число пар-ров, чем ПМ. Соответственно п(п-1+ т) параметров СМ не могут быть однозначно определены из птпар-ров ПМ. Чтобы получить единственно возможное решение для СМ, необходимо предположить, что некоторые из СК равны 0. Уменьшение числа СК модели возможно и другим путем: приравнивания некоторых коэффициентов друг к другу. Структурные модели можно подразделить на три вида: 1) Модель идентифицируема, если все структурные ее коэффициенты определяются однозначно, единственным образом по коэффициентам приведеннойформы модели, т.е. если число параметров структурной модели равно числу параметров приведенной формы модели. 2) Модель неидентифицируема, если число приведенных коэффициентов меньше числа структурных коэффициентов, и в результате структурные коэффициенты не могут быть оценены через коэффициенты приведенной формы модели. 3) Модель сверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов.
|
Вычтем
из уравнения (1) последнее и проведем
тождественные преобразования: Поскольку ut–случ. ошибка без автокорреляции, то для оценки пар-ров последнего ур-ния можно применять об. МНК. Если остатки по исходномуур-ию регрессии содержат автокорреляцию, то для оценки параметров ур-ния исп.обобщенный МНК:
1)
Преобразовать исходные переменные
yt
и хt
к виду 2) Применив обычный МНК к уравнению (2), определить оценки параметров а и b.
3)
Рассчитать пар-р а исх.ур-ния из
соотн-ния 4) Выписать исходное уравнение (1).
Если
значение кр.Дарбина–Уотсона близко
к 0, применение метода первых разностей
вполне обоснованно. Если
Аналогично
Поскольку
Следовательно,
В модели (3) мы определяем средние за два периода уровни каждого ряда, а затем по полученным усредненным уровням обычным МНК рассчитываем пар-ры а и b. Данная модель называется моделью регрессии по скользящим средним.
рассчитывается
из соотношения:
|
Если
в остатках полная отриц. автокорреляция,
то
Алгоритм выявления автокорреляции остатков по критерию Дарбина — Уотсона Выдвигается гипотеза об отсутствии автокорреляции остатков. Альтернативные гипотезы о наличии полож. или отриц. автокорреляции в остатках. Затем по таблицам определяютсякрит. значения кр. Д-УdL и du для заданного числа наблюдений n и числа независ. пер-ных модели k при уровне значимости α. По этим значениям промежуток [0;4] разбивают на 5 отрезков. Принятие или отклонение каждой из гипотез с вероятностью (1-α) рассматривается по следующей схеме:
Если расчетное значение кр.Д-У попадает в зону неопр-ти, то подтвержд.сущ-ниеавтокор-ции остатков и гипотезу отклоняют. Ограничения на применение критерия Дарбина – Уотсона. 1) он неприменим к моделям, включающим в качестве независимых переменных лаговые значения результативного признака, т.е. к моделям авторегрессии. Для тестирования на автокорреляцию остатков моделей авторегрессии используется h- критерий Дарбина. 2) методика расчета и использования критерия Д–У направлена только на выявление автокорреляции остатков первого порядка. При проверке остатков на автокорреляцию более высоких порядков следует применять другие методы. 3) критерий Д–Удает достоверные результаты только для больших выборок.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если
временной ряд имеет линейную тенденцию,
то его соседние уровни
и
Выбор
наилучшего уравнения в случае, если
ряд содержит нелинейную тенденцию,
можно осуществить путем перебора
основных форм тренда, расчета по
каждому уравнению скорректированного
коэффициента детерминации
|
|
Для
упрощения расчетов, удобнее работать
с отклонениями от средних уровней,
т.е.
|
Второй
шаг состоит
из двух подшагов. На первом из них,
который выполняется,
если число регрессоров уже больше
двух, делается попытка исключить один
из регрессоров. Ищется тот регрессор
Второй
подшагсостоит
в попытке включения нового регрессора
из исходного
набора предсказывающих переменных.
Ищем переменную
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
33. Построение аддитивной модели временного ряда Обратимся к данным об объёме потребления электроэнергии жителями за 4года. Табл1-расчет сезонной компоненты аддитивной модели
Шаг1.Проведём выравнивание исходных уровней ряда методом скользящей средней. Для этого:А)просуммируем уровни ряда последовательно за каждые 4 квартала со сдвигом на один момент времени и определим условные годовые объёмы потребления электроэнергии.(графа3)Б)разделив полученные суммы на 4,найдём скользящие средние.(графа4)В)приведем эти значения в соотв. с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних – центрированные скользящие средние.(графа5) Зам.Полученныевыр-ные знач. уже не содержат сез. комп.
Шаг2.найдём
оценки сез. компоненты как разность
между фактическими уровнями ряда и
цетрированными скользящими
средними.(графа6)Используем эти оценки
для расчёта значений сезонной
компоненты
Определим
корректирующий коэффициент: к =
Рассч.скорректир.зн-ниясез.
комп-ты как разность между ее ср.
оценкой и корректирующимкоэф-том
к:Si
=
Проверим условие равенства 0 суммы значений сез. комп. Расчетвыров.знач.тенд.Т и ошибок E отобразим в табл2. Первые 2 столбца этой табл такие же, как и в табл1. В 3 столбец внесемполуч.знач.сез. компоненты для каждого из кварталов. |
34. Построение мультипл. модели временного ряда Пусть имеются поквартальные данные о прибыли компании за последние четыре года.Рис показатели прибыли компании
Шаг1.Проведем выравнивание исх. уровней ряда методом скольз. средней. Шаг2.Найдем оценки сез. комп. как частное от деления фактических уровней ряда на центрир. скользящие средние (графа6). Используем эти оценки для расчета значений сезонной компоненты. Для этого найдем средние за каждый квартал оценки сезонной компоненты . Взаимопогашаемость сезонных воздействий в мультипликативной модели выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна числу периодов в цикле, т.е. четырем, так как в нашем случае число периодов одного цикла (год) равно четырем кварталам.
Поскольку
амплитуда сезонных колебаний
уменьшается, можно предположить
наличие мультипликативной модели.
Тогда получим корректирующий
коэффициент к =4/ Определим скорректированные значения сезонной компоненты, умножив ее средние оценки на корректирующий коэффициент к Sj= *k, где i = 1, ...,4.
|
35. Применение фиктивных переменных для моделирования сезонныхколебаний временного ряда Пусть имеется временной ряд, содержащий циклические колебания периодичностью к. Модель регрессии с фикт.временными для этого ряда будет иметь вид:
=a+b*t+
где Например, при моделировании сезонных колебаний на основе бальных данных за несколько лет число кварталов внутри одного года к=4,а общий вид модели следующий:
=a+b*t+
+ где ={ 1,для первого квартала 0, во всех остальных случаях. ={ 1,для второго квартала 0, во всех остальных случаях.
0, во всех остальных случаях. Уравнение тренда для каждого квартала будет иметь следующий вид
для
I квартала
= а
+ b-t
+
для
2 квартала у, = а
+ b-t+
для
III
квартала
= а
+ b-t
+
для IV квартала = а + b*t + ; Таким образом, фиктивные переменные позволяют дифференцировать величину свободного члена уравнения регрессии каждого квартала. Она составит: для I квартала а + для II квартала а + с2 для III квартала а + c3 для IV квартала а.
|
36.Моделирование тенденции временного ряда при наличии структурных изменений. Тесты Чоу и Гуйарати От сез. и циклич. колебаний следует отличать единовременные изменения характера тенденции врем.ряда, вызванные струк-ыми изменениями в экономике или иными ф-рами. В этом случае, начиная с некоторого момента времени, происходит изменение характера динамики изуч-ого пок-ля, что приводит к изменению пар-ров тренда, опис-щего эту динамику. Схематично такая ситуация изображена на рисунке 1.
Момент (период) времени t* сопров-ся значите-ыми изменениями факторов, оказывающих сильное воздействие на изучаемый показатель . Чаще всего эти изменения вызваны изменениями в обшеэкон. ситуации или факторам глобального характера, приведшими к изменению структуры эк-ки (например, начало крупных экономических реформ) Если исследуемый врем.ряд включает в себя соответствующий момент (период) времени, то одной из задач его изучения становится выяснение вопроса о том, значимо ли повлияли общие структурные изменения на характер этой тенденции.
Если
это влияние значимо, то для модел-ния
тенденции данного врем. ряда следует
использовать кус.-лин. модели регрессии,
т.е. разделить исходную сов-ть на две
подсов-ти (до момента времени
Каждый из описанных выше подходов имеет свои полож. и отриц. стороны. При построении кус.-лин. модели происходит снижение остат. суммы квадратов по сравнению с единым для всей сов-тиур-ем тренда. Однако разделение исх. сов-ти на 2 части ведет к потере числа наблюдений и, след-но, к снижению числа степеней свободы в каждом ур-нии кус.-лин. модели. Построение единого для всей сов-тиур-ния тренда позвол. сохранить число наблюдений n исходной сов-ти, однако остат. сумма квадратов по этому ур-нию будет выше по сравнению с кус.-лин. моделью. Очевидно, что выбор одной из двух моделей зависит от соотн-ния между снижением остат. дисперсии и потерей числа степеней свободы при переходе от единого ур-ния регрессии к кус.-лин. модели. Таблица 5.7 - Условные обозначения алгоритма теста Чоу
Зам. В рассматриваемой формулировке число параметров всех ур = = . В общем случае число параметров в каждом ур может различаться.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
37. Стохастические процессы. Основные определения. Эргодичность
Набор
случ. переменных X(t),
где
Мат.
ожидание E(Xt)
может
изменяться во времени и представляет
собой ф-ию среднего в зависимости от
времени:
Дисперсия
(Xt)
явл.
фун-ей, также зависящейот
времени:
В
общем случае в каждый момент времени
существует определенная дисперсия.
Автоковариация зависит
от каждого t1и
t2: Кон.реализация х1, х2, ..., хтдискр. стох. процесса Х 1, Х2, ..., Хт... явл. врем. рядом. Стох. процесс Xtназывается стационарным в сильном смысле, если совместное распределение вероятностей всех переменных Xt1,Xt2,...,Xtnточно то же самое, что и для переменных Xt1+ τ,Xt2+ τ,...,Xtn+ τ Под стационарным процессом в слабом смыслепонимается стох. процесс, для кот.среднее и дисп. независимо от рассм-ого периода времени имеют постоянное знач., а автоковариация зависит только от длины лага между рассм-ми переменными.
Автоковариация
как функция длины лага τназывается
автоковариационной функцией.
При τ=0 ее значение равно дисперсии. Проведя нормировку σ2=γ0 , получим автокорр. функцию стац. стох. процесса: ρτ= γτ/ γ0, где ρτϵ[-1,1] Временной ряд х1, х2, ..., хт, т.е. конкретная реализация стационарного стох. процесса Xtтакже называется стационарным. Экономические временные ряды представляют собой данные наблюдений за экономическими показателями, например, валовым внутренним продуктом, за ряд лет, и такие ряды, как правило, нестационарны.
|
38. Стохастические процессы. Особые случаи Набор случ. переменных X(t), где (вещ.числа) наз. стохастическим процессом. Стох. процесс Xtназывается стационарным в сильном смысле, если совместное распределение вероятностей всех переменных Xt1,Xt2,...,Xtnточно то же самое, что и для переменных Xt1+ τ,Xt2+ τ,...,Xtn+ τ Под стационарным процессом в слабом смыслепонимается стох. процесс, для кот.среднее и дисп. независимо от рассм-ого периода времени имеют постоянное знач., а автоковариация зависит только от длины лага между рассм-ми переменными. Особые случаи: Процесс наз. нормальным, если совместное распределение Xt1,Xt2,...,Xtn – это п-мерное норм.распределение. В этом случае из стационарности в слабом смысле следует стационарность в сильном смысле.
«Белым
шумом»наз.
чисто случайный процесс, т.е. ряд
незав., одинаково распределенныхслуч.
величин ai(iid).
Главные
свойства «белого шума» следующие:
1)μt=
E(at)
= const
= μ2)σ2t=
const
= σ2a3)
Из этого очевидным образом следует стационарность. «Белый шум» играет важную роль при моделировании остатков или шоков стохастического процесса, генерирующего данные (врем.ряд).
|
39. Стохастические процессы. Модели МА
Рассм.
процесс, явл. лин. комбинацией двух
элементов «белого шума», следующих
друг за кругом: Процесс скольз. ср. порядка q [МА (q)] – это процесс Xt = at - Q1at–1 – … –ϴqat–q,где at – «белый шум» μ = 0 Введем оператор лага или обр. действия L:
В
результате процесс
МА(q)
определяется
просто как
Процесс МА(q) имеет следующие свойства: 1) E[Xt] = 0
2)
3)
Среднее, дисперсия и ковариация не зависят от времени. Следовательно, процесс МА стационарен в слабом смысле.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Выдвинем гип.Но о структ.стаб-ти тенденции изуч.врем. ряда.
Остаточную
сумму квадратов по кус.-лин.модели(
Соответствующее
ей число степеней свободы
составит:
Тогда
сокращение остат. дисперсии при
переходе от единого ур тренда к
кус.-лин. модели можно определить
как:
Число
степеней свободы, соответствующее
с учетом соотношения (1) будет равно:
n-
-(n-
-
=
+ В соответствии с предлож. Г. Чоу методикой опред-ся значение F-кр. по следующим дисперсиям на одну степень свободы вариации:
F=
Найденное
значение F сравнивают с табл., получ.
по распред. Фишера для уровня знач-ти
а и числа ст. свободы
Если
F> Особенности применения теста Чоу.
1)
Если число параметров во всех уравнениях
(1), (2), (3) одинаково и равно k
то формула (2) упрощается:F=
2)
Тест Чоу позволяет сделать вывод о
наличии или отсутствии структ.
стабильности в изучаемом врем.ряде.
Если F<F_табл то это означает, что
уравнения (1) и (2) описывают одну и ту
же тенденцию, а различия численных
оценок их пар-ров
3) Прим. теста Чоу предполагает соблюдение предпосылок о норм.распр-нии остатков в ур-ниях (1) и (2) и нез-ть их распределений. Если гипотеза о структурной стабильности тенденции ряда отклоняется, дальнейший анализ может заключаться в исследовании вопроса о причинах этих структурных различий и более детальном изучении характера изменения тенденции. В принятых обозначениях эти причины обусловливают различия в оценках параметров уравнений (1) и (2). •Изменение численной оценки свободного члена ур тренда а2 по сравнению с а1 при условии, что различия между и статистически незначимы. Это означает, что прямые (1) и (2) параллельны. В данной ситуации можно говорить о скачкообразном изменении уровней ряда в момент времени t* при неизменном среднем абсолютном приросте за единицу времени; •изменение численной оценки параметра по сравнению с при условии, что различия между а1 и а2 статистически не значимы. Это означает, что прямые (1) и (2) пересекают ось ординат в одной точке. В этом случае изменение тенденции связано с изменением среднего абсолютного прироста временного ряда, начиная с момента времени t*, при неизменном начальном уровне ряда в момент времени t=0; •изменение числ.оценок пар-ров а1 и а2 также и . Она означает, что мнение характера тенденции сопровождается изменением как начального уровня ряда, так и среднего за период абсолютною прироста.
Один
из стат. методов тестирования при
применении численных ситуаций для
характеристики тенденции изучаемого
временного ряда был предложен Д.
Гуйарати. Этот метод основан на
включении в модель регрессии
фикт.перем. =а + b* +c*t + d*( *t) + ; (3) для каждого промежутка времени получим следующее уравнение Z =1 = (a +b) + (с + d) * t + ; (1)
Сопоставим полученные уравнения с уравнениями участков (1) и (2) а1=(а +b); b1= (с + d); a2=a b2= с. Парааметрb есть разница между свободными членами уравнений (1) и (2), а параметр d- разница между параметрами и ур (1) и (2). Оценка статистической значимости различий a1 и а2, а также и , эквивалентна оценке статистической значимости параметров b и d (5,9), Эту оценку можно провести при помощи t-критерия
Таким
образом, если в уравнении (3) b явл
стат.знач., a d — нет, то изменение
тенденции вызвано только различиями
пар-ров а1 и а2. Если в этом ур-нии пар.
d статистически значим, а b - незначим,
то изменение характера тенденции
вызвано различиями параметров
и
.
Наконец, если оба коэффициента b
и d явл статистически значимыми, то
на изменение характера тенденции
повлияли как различия между а1 и а2,
так и различия между
и
Основное его преимущество перед тестом Чоу состоит в том, что надо построить только одно, а не три уравнений тренда.
|
Параметр b в этой модели характеризует среднее абсолютное изменение уровней ряда под воздействием тенденции. В сущности, модель (1) есть аналог аддитивной модели временного ряда, поскольку фактический уровень временного ряда - это сумма трендовой, сезонной и случайной компонент. |
Проверим условие равенства 4 суммы значений сез. комп. Занесем полученные значения в новую таблицу для соответствующихкварталов каждого года (графа 3, табл2).
Шаг3.Разделим каждый уровень исходного ряда на соотв. значения сез. компоненты. Получим: Т* Е = Y/S (графа 4), кот.содержат только тенденцию и случ. компоненту.
Шаг4.
Определим комп. Т в мультипл. модели.
Для этого рассчитаем пар-рылин. тренда,
используя уровни (Т*Е). Нашли:
T=константа-коэф. регрессии*t, (1).
Подставив в это урзн-ния t= Шаг5.Найдем уровни ряда по мультипл. модели, умножив уровни Т на соотв-щие значения сез. компоненты (графа 6) Шаг6.Расчет ошибки в мультипл. модели произв-ся по -леЕ = Y/(T*S).Численные значения ошибки приведены в графе 7. Если временной ряд ошибок не содержит автокорреляции, его можно использовать вместо исходного ряда для изучения взаимосвязи с другими временными рядами. Для того чтобы сравнить мультипликативную модель с другими моделями временного ряда, можно по аналогии с аддитивной моделью использовать сумму квадратов абсолютных ошибок. Абсолютные ошибки в мультипликативной модели определяются как: E_абс= -(T*E) Пусть необходимо сделать прогноз ожидаемой прибыли по данным этого примера компании за первое полугодие ближайшего следующего года.
Прогнозное
значение
|
Шаг3.Исключим влияние сезонной компоненты, вычитая ее значение из каждого уровня исходного временного ряда. Получим величины Т+Е= Y-S. (графа 4, табл2). Шаг4.Определим компоненту данной модели. Для этого проведем аналитическое выравнивание ряда (Т+Е) с помощью линейного тренда. Нашли: T=константа+коэффициент регрессии*t, (1)
Подставив в ур (1) значения t= , найдем уровни тенденции T для каждого момента времени(графа5). Шаг5. Найдемзнач-ияур. ряда, полученные по аддит. модели. Для этот прибавим к уровням Т значения сез. комп. для соотв-щих кварталов (графа 6). Шаг6. В соответствии с методикой построения аддит. модели расчет ошибки пров-ся по ф-ле:Е=Y-(Т+S)Эго абсолютная ошибка. Численные значения абсолютных ошибок приведены в графе7. По аналогии с моделью регрессии для оценки качества построения модели,а также для выбора наилучшей модели можно исп. сумму квадратов абс. ошибок. Пусть требуется дать прогноз. Прогнозное значение F, уровня временного ряда в аддитивной модели в соответствии с соотношением Y=T+S+E - это сумма трендовой и сезонной компонент. Объем электроэнергии, потребленной в течение первого полугодия ближайшего следующего, т.е. пятого, года, рассчитывается как сумма объемов потребления электроэнергии в I и во II кварталах пятого года, соответственно и .Для определения трендовой компоненты воспользуемся уравнением тренда (1). Получим и .Значения сезонной компоненты равны и Значит: = + , = +
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Эргодичность: Осн. проблема в оценивании параметров распределения стох. процесса состоит в том, что в общем случае размер выборки п=1, поскольку обычно имеется единств. реализация процесса. Ввиду этого сделать осмысленную оценку практически невозможно. Изучаемый стох.процесс как таковой неизвестен. Его стац-сть или нестац-сть м/б установлена только посредством анализа соответствующего ему врем.ряда. Но, с др. стороны, многие методы анализа врем.рядов предполагают их стац-сть. Это приводит к своего рода замкнутому кругу, когда свойство, на наличие кот.проводится исследование, входит в изначальные предпосылки. Данную проблему можно решить с использованием понятия эргодичность: это поведение большого класса стационарных процессов, когда ср. арифм. со временем сходится к мат. ожиданию. Эргодичность делает возможным оценивание μ, σ2, γ(τ) стох. процесса только по его реализации – врем.ряду. Известны различные подходы к распознаванию стационарности временных рядов: 1) граф.представл. врем. ряда и визуальная проверка на наличие к-либо тренда 2) исследование на наличие автокорр. в реальных данных; 3) тесты на присутствие детерминистического тренда, например t-тест на коэффициенты оценок МНК; 4) тесты на наличие стох. тренда, например тесты на единичный корень.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
40. Стохастические процессы. Модели AR. Проблема стационарности Авторегрессионный процесс порядка р[АR(p)] – стох. процесс Xt:
Используя функцию оператора лага:
Процесс AR не всегда стационарен. Если мы знаем представление вида (1) или (2) данного процесса, то выяснить вопрос о стационарности процесса можно с помощью так называемом.характер. уравнения.
Необх. и достат. условием стационарности AR процесса явл. след.: AR-процесс является стационарным тогда и только тогда, когда его комплексные решения (корни) лежат вне единичного круга, т.е. |z| > 1. В частности, если |z| = 1, процесс называется процессом единичного корня и является нестационарным.
|
31. ВР–это совокупность знач. к-либо показателя за несколько последовательных моментов или периодов времени. Каждый уровень ВР формируется под воздействием большого числа факторов, кот. условно можно разделить на 3 группы:факторы, формирующие тенденцию ряда;факторы, формирующие циклические колебания ряда;случайные факторы. При различных сочетаниях в изучаемом явлении факторов зависимость уровней ряда от времени может принимать различные формы. Во-первых, большинство ВР эконом. показателей имеют тенденцию, характ-щую совокупное долговременное воздействие множества факторов на динамику изучаемого показателя. Во-вторых, изучаемый показатель может быть подвержен циклическим колебаниям. Эти колебания могут носить сезонный характер, поскольку экономическая деятельность ряда отраслей экономики зависит от времени года. В большинстве случаев фактический уровень ВР можно представить как сумму или произведение трендовой, циклической и случайной компонент. Модель, в кот. ВР представлен как сумма перечисленных компонент, называется аддитивной моделью ВР. Модель, в кот. ВР представлен как произведение перечисленных компонент, наз. мультипликативной моделью ВР. Основная задача эконометрического исследования от дельного ВР - выявление и придание количественного выражения каждой из перечисленных выше компонент с тем, чтобы использовать полученную информацию для прогнозирования будущих значении ряда или при построении моделей взаимосвязи двух или более ВР АВТОКОРРЕЛЯЦИЯ УРОВНЕЙ ВРЕМЕННОГО РЯДА И ВЫЯВЛЕНИЕ ЕГО СТРУКТУРЫ.При наличии во ВР тенденции и циклических колебаний значения каждого последующего уровня ряда зависят от предыдущих. Корреляционную зависимость между последовательными уровнями ВР наз. автокорреляцией уровней ряда. Коли-нно ее можно измерить с помощью линейного коэффициента корреляции между уровнями исходного ВР и уровнями этого ряда, сдвинутыми на несколько шагов во времени.
Коэффициента
корреляции :
В качестве переменной х мы рассмотрим ряд у2,…, уп, в качестве переменной у - ряд у1, у2, …, уп –1.
|
41 Стохастические процессы. Модели ARMA. Представление в виде бесконечных МА и AR процессов. Набор случ. эл-товX(t), где t€θсR(веществ.числа) наз. стохастич. процессом (СП). Дискр. СП опр-тся как посл-ть случ. переменных X (t) в дискр. моменты вр. t= t1, t2, ..., tТ Мат. ожид. E(Xt) может изменяться во времени т.е. явл. ф-цией среднего от врем. μt = E[Xt] Также и дисперсия σt2 = E[(Xt– μt)2](в каждый момент времени сущ. опр-ная дисп) Хар-кой случ. процесса явл. автоковариация γt1,t2 =cov(Xt1, Xt2) = E[(Xt1- μt1)(Xt2- μt2)]. В общ.виде зависит от каждого t1и t2. СП Xtназ. стационарным в сильном смысле, если совместное распр-ние вероятностей всех переменных Xt1, Xt2,…,Xtnто же самое, что и для переменных Xt1+τ, Xt2+τ,…,Xtn+τ.Cтац. в слабом смысле наз. СП, для кот.среднее и дисперсия независит от момента измерения, а автоковар. зависит только от длины лага между переем, т.е. μt=μ = const; σt2= σ= const; γt1,t2= γt2–t1= γτ, где τ= t2 - t1(лаг) Число периодов, по кот.рассчитывается коэф. автокоррел. наз.лагом. Автоковар. как ф-ция длины лага τ наз. автоковар. функцией, т.е. γ(τ) = γτ= E[(Xt- μ)(Xt-τ – μ)]. Для дискр. процессов, т.к. t=1, 2,…,T величина лага также м.б. дискр., т.е. τ=1,2,… и τ0=σ2 . Автокорреляц. ф-ция им. вид: ρτ=γτ/γ0При этом ρτ€[-1;1] явл. безразм. величиной. Замеч. 1) СПстацион. в сильн. см. всегда стацион-рен в слаб.– обр. не верно; 2) Если процесс Xt– стационарен, то его реал-ция (ВР) также стац-рна.. На практике стац-сть ВР означает отсутствие: ·тренда; ·систематич. изм. дисп; ·строго периодичных флуктуаций; ·автокорр. и автоковар. ВР. Смесь процессов авторегрессии и скользящего среднего (AR и МА) порядков ри qсоответственно называется авторегрессионным процессом скользящего среднего [ARMA(p,q)]:
|
42. Оценка структуры стационарного процесса. Автокорреляционная функция Согласно определению автокорреляционная функция (ACF) определяется след образом: ρ τ = γτ/ γ0 = Е [(Xt– μ ) * (Xt+1 – μ )] / γ0. График ρτназ-етсякоррелограммой. Определенная форма автокорреляционной ф-ции является хар-кой определенных видов ARMA-процессов. В связи с этим такие ф-ции используются при анализе ВР для определения типа и порядка процесса, а также соответствующей модели. Для процесса AR(p) коррелограмма представляет собой смесь экспоненциальной кривой и синусоиды. Пример 1. Пусть Xt — процесс AR(1) без свободного члена с φ1<1 – стацион процесс, т.е из Xt= φ1xXt-1 + at=>Xt2=(φ1 Xt-1 + at)2 = φ12 X2t-1 + 2 φ1Xt-1 at+ at2 => γ0 =E(Xt2) = φ12 γ0 + 0 + σa2, откуда: γ0 = σa2 / (1 –φ21). Для вычисления γ1рассмотрим Xt-1 = φ1Xt-2 + at-1. Тогда XtXt-1 = (φ1 Xt-1 + at) Xt-1 = φ1 X2t-1 + Xt-1 at. Т.о. получим:γ1=E (XtXt-1) = φ1 E (X2t-1) + 0 = φ1σa2 / (1 -φ21). Из этого следует, что ρ1=φ1. В общем виде получается геометрическая прогрессия: ρk= φ1k В кач-ве оценки автоковариационной ф-ции эргодического процесса, сгенерировавшего временной ряд Xtможно применять:
В разных источниках используются либо 1-ая либо 2-ая. Очевидно, что при Т>>τ различие между оценками исчезает. Оценка автокорреляционной функции
,где sx2- выборочная дисперсия полученного ВР.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
43. Нестационарные временные ряды. Метод разностей и интегрируемость. Реальные временные ряды, харак-щиеэкон-ие процессы, как правило не стационарны. Обычно эти ВР содержат тренд (возраст-щий, убыв) илиимеют колебания на фоне общего тренда. Также возможно наличие гетероскедастичности и изменяющейся автокорреляции. Ряд нестационарен, если среднее или дисперсия данного ряда изменяются во времени, а также если ковариация зависит от конкретных моментов времени ее изменения.. Типичные примеры ВР: ставка обменных курсов индустриально развитых стран, напр, доллора и йеней, показатели ВВП и тд. Для реальных эконом. процессов осн причиной, вызывающей нестационарность ВР, является высокая инерционность внезапного воздействия (шока) на ВР. Во время эконом-ого спада или бума основные макроэконом-ие показатели имеют сильные изменения и остаются на новом уровне в течение длительного промежутка времени, не возвращаясь к своему прежнему положению. Для получения критерия, который м.б. бы использовать для выявления нестационарности рядов, рассмотрим авторегрессионный процесс Ytпервого порядка: Yt=α0+α1Yt-1+ε t. Между стац и нестац ВР имеется существенное отличие – единовременное шоковое воздействие на стацион-ый ряд носит временный хар-ер.Со временем эффект рассеивается, и значения временного ряда возвращаются к своему долгосрочному среднему значению. След-но, долгосрочный прогноз стационарного ряда сходится к безусловному среднему. Для облегчения идентификации стационарных рядов будем использовать след св-ва: 1.Уровни ряда колеблются вокруг постоянного долгосрочного среднего значения. 2.Временной ряд имеет постоянную, не зависящую от времени дисперсию. 3.Временной ряд имеет теоретическую коррелограмму, которая убывает при возрастании длины лага. |
44 Оценка порядка интегрируемости. Тесты на единичный корень. Интеграционная статистика Дарбина-Уотсона
Интеграционная
статистика Дарбина-Уотсона явл
наиболее
простым способом проверки на
стационарность ВР Интегр статистика
Д-У (IDW)
разработана для авторегрессии
первого пор Yt=α1Yt-1+ε t.(1).
Данная статистика
имеет
след вид:
|
49 Изучение структуры лага и выбор вида модели с распределенным лагом. Модели Алмон. Текущие и лаговые значения факторной переменной оказывают различное по силе воздействие на результативную переменную модели. Количественно сила связи между результатом и значениями факторной переменной, относящимися к различным моментам времени, измеряется с помощью коэффициентов регрессии при факторных переменных. Если построить график зависимости этих коэффициентов от величины лага, можно получить графическое изображение структуры лага, или распределения во времени воздействия факторной переменной на результат. Структура лага может быть различной. Графический анализ структуры лага аналогичным образом можно проводить и с помощью относительных коэффициентов регрессии βj. Основная трудность в выявлении структуры лага состоит в том, как получить значения параметров bj (или βj). Выше уже отмечалось, что обычный МНК редко бывает полезным в этих целях. Поэтому в большинстве случаев предположения о структуре лага основаны на общих положениях экономической теории, на исследованиях взаимосвязи показателей либо на результатах проведенных ранее эмпирических исследований или иной априорной информации.
Лаги
Алмон. Рассм.
общую модель с распределенным лагом,
имеющую конечную максимальную
величину лага l,
которая описывается соотношением
Формально модель зависимости коэффициентов bj от величины лага j в общем виде для полинома k-й степени имеет вид: bj = с0 + c 1 j + c2j2+...+ ck jk. В данной модели предполагается, что степень полинома k меньше максимальной величины лага l.
|
50 Изучение структуры лага и выбор вида модели с распределенным лагом. Метод Койка. Текущие и лаговые значения факторной переменной оказывают различное по силе воздействие на результативную переменную модели. Количественно сила связи между результатом и значениями факторной переменной, относящимися к различным моментам времени, измеряется с помощью коэффициентов регрессии при факторных переменных. Если построить график зависимости этих коэффициентов от величины лага, можно получить графическое изображение структуры лага, или распределения во времени воздействия факторной переменной на результат. Структура лага может быть различной. Графический анализ структуры лага аналогичным образом можно проводить и с помощью относительных коэффициентов регрессии βj. Основная трудность в выявлении структуры лага состоит в том, как получить значения параметров bj (или βj). Выше уже отмечалось, что обычный МНК редко бывает полезным в этих целях. Поэтому в большинстве случаев предположения о структуре лага основаны на общих положениях экономической теории, на исследованиях взаимосвязи показателей либо на результатах проведенных ранее эмпирических исследований или иной априорной информации. Метод Койка. Допустим, что для описания некоторого процесса используется модель с бесконечным лагом вида: yt = а + b0-xt + b1-xt – 1 + b2-xt – 2 + ... + εt (1) Очевидно, что параметры такой модели обычным МНК или с помощью иных стандартных статистических методов определить нельзя, поскольку модель включает бесконечное число факторных переменных. Однако, приняв определенные допущения относительно структуры лага, оценки ее параметров все же можно получить. Эти допущения состоят в наличии геометрической структуры лага, т.е. такой структуры, когда воздействия лаговых значений фактора на результат уменьшаются с увеличением величины лага в геометрической профессии.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
или
Новая информация момента времени t сод.только в одном слагаемом at. Процесс ARMA(p,q) может быть записан коротко:Фр(L)Xt=φ0+Θq(L)at , где Фр(L) и Θq(L) ф-ции операторов лага соответствующих AR(р) и МА(q)процессов, а φ0, как правило, предполагается=0. При очень общих условиях стационарный ARMA-процесс Фр(L)Xt=φ0+Θq(L)at м/б представлен как бесконечный AR-процесс или как бесконечный МА-процесс:
или
Бесконечный полином лага Ψ(L) определяется выражением: Ψ(L)=Θq(L)/Фр(L) В частности, стационарные AR-процессы м/б представлены как бесконечные МА-процессы, а большинство МА-процессов (при условии обратимости) — как бесконечные AR-процессы. При анализе реальных временных рядов следует выбирать представление процесса с наименьшим возможным числом параметром. ARMA-процессы имеют более сложную структуру по сравнению со схожими по поведению AR- или МА-процессами в чистом виде, но при этом ARMA-процессы характеризуются меньшим количеством параметров, что является одним из их преимуществ.
|
Тогда
Число периодов, по кот. рассчитывается коэффициент автокорреляции, называют лагом. С увеличением лага число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается. Свойства коэффициента автокорреляции. он строится по аналогии с линейным коэффициентом корреляции и таким образом характеризует тесноту только линейной связи текущего и предыдущего уровней ряда. Поэтому по коэффициенту автокорреляции можно судить о наличии линейной (или близкой к линейной) тенденции. по знаку коэффициента автокорреляции нельзя делать вывод о возрастающей или убывающей тенденции в уровнях ряда. Большинство ВР экономических данных содержит положительную автокорреляцию уровней, однако при том могут иметь убывающую тенденцию. Последовательность коэффициентов автокорреляции уровней первого, второго и т.д. порядков называют автокорреляционной функцией ВР. График зависимости ее значений от величины лага (порядка коэффициента автокорреляции) называется коррелограммой. Анализ автокорреляц. ф-ции и коррелограммы позволяет определить лаг, при кот. автокоррел. наиболее высокая, а след, и лаг, при кот. связь между текущим и предыдущими уровнями ряда наиболее тесная.
Если
наиболее высоким оказался коэффициент
автокоррел. 1- порядка, исследуемый
ряд содержит только тенденцию. Если
наиболее высоким оказался коэффициент
автокоррел. порядка
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Изложенный подход был предложен Л.М. Койком. Он предположил, что существует некоторый постоянный темп λ (0 <λ< 1) уменьшения во времени лаговых воздействий фактора на результат. Если, например, в период t результат изменялся под воздействием изменения фактора в этот же период времени на b0 ед., то под воздействием изменения фактора, имевшего место в период t - 1, результат изменится на b0 λ ед.; в период t - 2 -на b0 λ λ= b0 λ2 ед. и т.д. Для некоторого периода t – l это изменение результата составит: b0 λl ед. В более общем виде можно записать: bj = b0 λ j; j = 0, l, 2,..., 0 < λ < 1. (2) Ограничение на значения λ > 0 обеспечивает одинаковые знаки для всех коэффициентов bj > 0, а ограничение λ < 1 означает, что с увеличением лага значения параметров модели (1) убывают в геометрической прогрессии. Чем ближе λ к 0, тем выше темп снижения воздействия фактора на результат во времени и тем большая доля воздействия на результат приходится на текущие значения фактора xt. Выразим с помощью формулы (2) все коэффициенты bj в модели (1) через b0 и λ: уt = а + b0 xt + b0 λ xt – 1 + b0 λ2 xt – 2 + … + εt Тогда для периода t – 1 эта модель примет вид: уt – 1 = а + b0 xt – 1 + b0 λ xt – 2 + b0 λ2 xt – 3 + … + εt – 1 . Умножим обе части этого уравнения на λ и Вычтем найденное соотношение из соотношения для yt: yt – λ y t – 1 = a – λ a + b0 xt + εt – λ εt – 1 В результате преобразований мы получаем модель Койка: yt = a (1 – λ) + b0 xt +(1 – λ) y t – 1 ut где ut = εt – λ εt – 1. Полученная модель — это модель двухфакторной линейной регрессии (точнее – авторегрессии). Определив ее параметры, найдем λ и оценки параметров а и b0 исходной модели. Далее c помощью соотношений (2) несложно определить параметры b1, b2,... модели (1). Описанный выше алгоритм получил название «преобразования Койка». Это преобразование позволяет перейти от модели с бесконечными распределенными лагами к модели авторегрессии, содержащей две независимые переменные хt и yt – 1.
|
Тогда каждый из коэффициентов bj модели (1) можно выразить следующим образом: b 0 = c0 ; b1 = c 0 + c1 + c2 + …+ ck ; b2 = c0 + 2c1 + 4c2 + …+ 2kck ; b3 = c0 + 3c1 + 9c2 + …+ 3kck ; … (2) Подставив в (1) найденные соотношения для bj и перегруппировав получим: yt = а + с0 хt + с0 (хt + хt – 1+ ... + хt – l) + с1 (хt – 1 + 2хt – 2+ 3хt – 3+... + l хt – l) + с2 (хt – 1 + + 4 хt – 2+ 9 хt – 3+... + l2 хt – l) + … + сk (хt – 1 + 2k хt – 2+ 3k хt – 3+... + lk хt – l) + εt . (3) Обозначим слагаемые в скобках при ci как новые переменные: z0 = хt + хt – 1+ ... + хt – l z1 = хt – 1 + 2хt – 2+ 3хt – 3+... + l хt – l z2 = хt – 1 + 4 хt – 2+ 9 хt – 3+... + l 2 хt – l …… zk = хt – 1 + 2k хt – 2+ 3k хt – 3+... + l k хt – l (4) Перепишем модель (3) с учетом соотношений (4): yt = а + с0 z0 + с1 z1 + с2 z2 + … + сk zk + εt. (5) Процедура применения метода Алмон для расчета параметров модели с распределенным лагом выглядит следующим образом.
|
|
Метод разностей и интегрируемость. Большинство экон-их ВР нестационарны, но многие методы и модели основаны на предположении о стационарности ВР. Во многих случаях взятие разностей временных рядов позволяет получить стационарные ВР. Т.е. вместо знач-ияур-ни Х1, Х2, …, Хnрассм их разность: ΔХ1=Х2-Х1, ΔХ2=Х3-Х2 и тд.Первые разности стохастического процесса имеют вид: (1-L)Xt=ΔXt=Xt- Xt-1. Или для сезонного процесса с длиной периода s: (1-Ls)Xt=ΔsXt=Xt- Xt-sЕсли первые разности ряда xtстационарны, то ряд xtназывается интегрируемым первого порядка. В противном случае дальнейшее взятие разностей приведет ко вторым разностям: (1-L)2Xt=Δ2Xt =ΔXt- ΔXt-1. Если этот ряд стационарен, то ряд xtназывается интегрируемым второго порядка. Если мы получаем первый стационарный ряд после k-кратного взятия разностей, процесс называется интегрируемым к-гопорядка.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
45 Оценка порядка интегрируемости. Тесты Дики-Фуллера Тесты Д-Ф служат для определения порядка интегрируемости процесса Yt=α1Yt-1+ε t (1). Основная идея метода заключается в проверке гипотезы о стационарности процесса и последовательных его разностей повышающегося порядка. Зам. Если проводить оценку пар-ра α1 ур-ия (1) обычным МНК и проверять гипотезу о равенстве α1=1 с помощью t-статистики, м. получить ложную значимость, т.к в рамках нулевой гипотезы t-теста Стьюдента оцениваемое знач-ие д.б стационарно. Тест Д-Ф (DF-тест) использует нулевую гипотезу, кот предполагает нестационарность процесса, т.е основан на оценке параметра δ=α1-1 уравнения ΔYt=Yt-Yt-1=δYt-1+ε t (2). (2) эквив-на (1), при этом Н0: состоит в проверке факта, что δ=0; Н1: что δ<0. Если Н0 отклоняется в пользу альтернативной, то делаем вывод, что α1<1, т.е процесс Yt — стац-ый, или интегрируемый нулевого порядка. Поскольку распределение статистики Д-Ф не имеет аналитического представления, существуют некоторые сложности с определением точного критического значения для DF-теста. Таблицы теста Д-Ф на порядок интегрируемости, рассчитанные для обычных уровней значимости в 1, 5, 10%. Эти значения эмпирические, а не теоретические, поэтому в таблице крит-их знач-ий указаны верхнее и нижнее пороговые значения. (Указ-ые в табл знач-ия DF-теста отриц-ны).
|
46
Если в остатках t
наблюдается автокорреляция, то рез-ты
обычного МНК будут недостоверны. Для
решения этой проблемы Дики и Фуллер
предложили включить в правую часть
дополнительные объясняющие переменные:
лаговые значения переменной из левой
части
Yt=α1Yt-1+ε
t
(1),
т.е.
|
47 Модели ARIMA. Идентификация модели и оценивание пар-ров. Пусть Xt — нестац-ный процесс со стац-ными разностями d-го порядка, т.е. Yt=dXt - стац процесс, а d-1Xt — нестац, т.е Xt - интегрируем d-го порядка.
Если
Yt
уже стац-ый (процесс ARMA(p, q)), т.е.
|
48 Общая хар-ка моделей с распределенным лагом и моделей авторегрессии. Интерпретация пар-ов моделей с распределенным лагом и моделей авторегрессии.
М.
выделить два основных типа динамических
эконометрических моделей: 1)модели
авторегрессии; 2)модели с распределенным
лагом. Для этих моделей знач-ия
переменной за прошлые периоды времени
непосредственно включены в модель.
В эти модели включены переменные,
хар-ющие ожидаемый или желаемый
уровень рез-та, или один из факторов
в момент времени t. При исследовании
экономических процессов нередко
приходится моделировать ситуации,
когда значение результативного
признака yt
в текущий момент времени t формируется
под воздействием ряда факторов t–1,
t-2,..., t–l.
Эконометрическое моделирование
осуществляется с применением моделей,
содержащих не только текущие, но и
лаговые значения факторных переменных.
Эти модели наз моделями
с распределенным лагом.
Прим: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Данная модель
говорит о том, что если в некоторый
момент
времени t происходит изменение незав-ой
переменной х, то это изменение будет
влиять на значения переменной у в
течение p следующих моментов времени.
Коэф-т регрессии b0
хар-ет среднее абсолютное изменение
yt
при изменении xt
на одну единицу в данный фиксированный
момент t, поэтому его наз краткосрочным
мультипликатором.
Введем обозначения βj
=
bj
/
b,
j=0,1,2…
βj
– относительные
коэф-ты модели с распр лагом.
Для любого у
0 < βj
<1
и ∑ βj=1.
В этом случае j
явл весами
для соотв-щих коэф-ов bj.Используя
j
можно определить дополнит хар-ки:
1)вел-ну среднего лага: Обратимся теперь к модели авторегрессии: . Вел-на bo хар-ет краткосрочное изменение yt под воздействием изменения xt на 1 ед. Общие абсолютные изменения рез-та в момент t+1 составит b0с1 единиц, в (t+2) – b0с12 ед и т.д. След-но b = b0 + b0 cl + b0 cl2 + b0 сl3+... Для реализации стабильности ур-ия yt очевидно необх-мо |с1|<1. Тогда учитывая св-во суммы бескон геом прогрессии получим b=b0/(1-c1). Данная интерпитация предполагает наличие бесконечного лага.
|
Шаг
4.
Выбор наиболее подходящей модели
среди оцененных: – анализ остатков,
которые д. иметь св-ва белого шума; –
рассмотрение модели, наилучшим образом
воспроизводящей конкретный ВР, и ее
наиболее экономичною с точки зрения
кол-ва пар-ров. При сравнении различных
моделей для одного и того же ВР имеем
дело с несколькими конкурирующими
целями: 1. для МНК — минимизация
дисперсии ошибок и минимизация числа
пар-ров модели; 2. для МПМ — максимизация
ф-ции правдоподобия при минимизация
числа пар-ров модели. Обычно оцениваемая
модель лучше соотв-ет ВР при более
высоких порядках p
и q модели ARMA, но это приводит к
усложнению модели. Для нахождения
компромисса используются
информационный критерий Акаики и
критерий Шварца. Кр. Акаики:
где
a2—
дисперсия ошибок; lmax(T,p,q)
— логарифмическая функция правдоподобия
модели ARMA с коэф-ами р и q соотв-но. Кр.
Шварца:
|
. Информационные критерии могут быть рассчитаны по следующим формулам:
Из двух моделей в определенном смысле лучше та, для которой значение AIC (и SC) ниже, a AICL (и SCL) выше. SC-критерий отбирает более экономичные модели.
|
Для проверки ВР уt на порядок интегр-ти рассчитывают значение t-статистики Стьюдента для пар-ра δ и сравнивают его с верхним и нижним пороговыми значениями DF-статистики из таблицы. Если расчетное знач-ие t меньше, чем нижнее крит-ое знач-ие при данном числе наблюдений n, то для Н0: δ=0 отклоняем, т.е принимаем альтернативную о стационарности процесса yt. Если расчетное значение t-статистики превышает верхнее критическое значение, тогда нулевая гипотеза не м.б отклонена, процесс нестац-ый. В случае, когда расчетное критическое значение попадает в область между верхним и нижним критическими значениями, ничего определенного об отклонении или принятии нулевой гипотезы сказать нельзя. Если тест показал наличие стац-ти ->проводится оценка о наличии интегрируемости первого порядка, т.е.DF-тест применяется к первым разностям. Ур-ние (2) примет вид: ΔΔYt=δΔYt-1+εt. Снова выдвигаем две гипотезы: Н0 : δ=0 (процесс нестац); Н1 : δ<0 (стац). Если на основе DF-теста отклоняем Н0 и принимаем Н1, то процесс Yt интегрируем первого порядка (имеет один единичный корень). Если Н0 неотклон-ся, то проверяют процесс на интнгрируемость второго пор. и т.д. Сущест-ют формы для DF-теста для оценки порядка интегр-ти случая процесса со смещением: Yt= α0 +α1Yt-1+ε t, где α0 - свободный член(смещение). Механизм оценки аналогичен описанному выше, за исключением применяемой таблицы.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

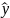 = f ( x ), где у - зависимая переменная, а
х - независимая, или объясняющая
переменная.
= f ( x ), где у - зависимая переменная, а
х - независимая, или объясняющая
переменная.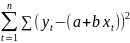 (1)
(1)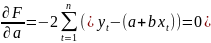
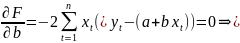
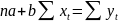 и
и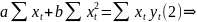
 (3),
(3),
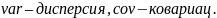
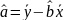 (4)
(4)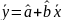 т.е.
прямая регрессии полученная
в результате минимизации функционала
(1) проходит через точку (
т.е.
прямая регрессии полученная
в результате минимизации функционала
(1) проходит через точку (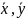 ).
).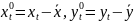 отклонения от средних по выборке (где
отклонения от средних по выборке (где
 ).
Получим линейную регрессии для
выборки, т.е. подберем линейную функцию
).
Получим линейную регрессии для
выборки, т.е. подберем линейную функцию
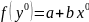 ,
минимизирующую функционал
,
минимизирующую функционал
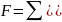 .
.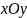 ,
что и для исходных данных
,
что и для исходных данных
 ,
только начало координат переместится
в точку
,
только начало координат переместится
в точку
 ).
Проделав
вычисления (т.е. нахождение выборочных
характеристик
).
Проделав
вычисления (т.е. нахождение выборочных
характеристик
 )
заменим
на
)
заменим
на
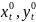 и
учитывая,
что
,
получим:
и
учитывая,
что
,
получим:
 =0,
=0,
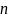 пар измерений
пар измерений
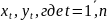 .
Рассмотрим
-мерное векторное пространство
.
Рассмотрим
-мерное векторное пространство
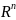 ,
в котором определено скалярное
произведение векторов
,
в котором определено скалярное
произведение векторов
 ,
где
,
где
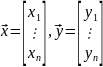 ,
,
 Так же введем единичный вектор
Так же введем единичный вектор
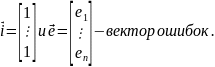 ,
где
,
где
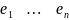 -
отклонение данных от линии регрессии,
кот . определ. из вектора
-
отклонение данных от линии регрессии,
кот . определ. из вектора
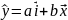 ,
,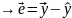
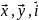 .
На вектора
.
На вектора

 натянем плоскость
натянем плоскость
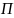 .
При этом вектор
.
При этом вектор
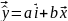 может находится в плоскости П
может находится в плоскости П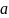 и
и
 ,
чтобы
вектор
,
чтобы
вектор
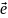 имел
наименьшую длину (т.е.
имел
наименьшую длину (т.е.
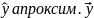 ).
Очевидно,
что решением является максим.
).
Очевидно,
что решением является максим.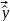 для
кот. вектор
перпендикулярен
плоскости
.
Для
этого необходимо
и достаточно, чтобы вектор
был
ортогонален векторам
и
.
Признаком ортогональности явл.
для
кот. вектор
перпендикулярен
плоскости
.
Для
этого необходимо
и достаточно, чтобы вектор
был
ортогонален векторам
и
.
Признаком ортогональности явл.
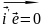 и
и
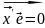 .
.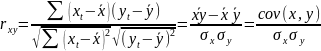 (1)
(1)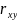 очевидна взаимосвязь:
очевидна взаимосвязь:
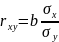 ,
,
 .(2)
.(2)
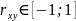
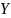 ,
объясняемую регрессией, в общей
дисперсии результативного признака.
,
объясняемую регрессией, в общей
дисперсии результативного признака.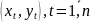 построено эмпирическое ур-ие регрессии
построено эмпирическое ур-ие регрессии
 .Тогда
наблюдаемые значения
.Тогда
наблюдаемые значения
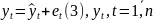 -
теоретич. знач.результатов регрессии,т.е
точки соответств.
-
теоретич. знач.результатов регрессии,т.е
точки соответств.
 ,
лежащие на линии регрессии. Вычтем
из (3)
,
лежащие на линии регрессии. Вычтем
из (3)
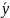 :
: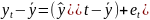 или
или
 (4)где
(4)где
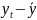 -отклонение
-отклонение
 -ой
наблюд. точки от сред. знач.;
-ой
наблюд. точки от сред. знач.;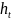 -
отклонение
-ой
от линии регрессии. Возведем(4) в
квадрат и просуммируем по
:
-
отклонение
-ой
от линии регрессии. Возведем(4) в
квадрат и просуммируем по
:
 Для случая парной регрессии
Для случая парной регрессии
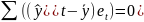
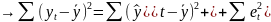 (5),
т.е. полная сумма квадратов
(5),
т.е. полная сумма квадратов
 может
интерпретироваться как мера общего
разброса результат. признака равна
сумме соответ. мер разброса, объясняемого
с помощью регрессии и остат. суммы
квадратов.
может
интерпретироваться как мера общего
разброса результат. признака равна
сумме соответ. мер разброса, объясняемого
с помощью регрессии и остат. суммы
квадратов.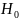 о
том , что между
о
том , что между
 зависимость отсутствует или фактор
зависимость отсутствует или фактор
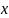 не влияет
на результат у
не влияет
на результат у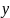 от среднего
на две части объяснен. и необъяснен.
Известно что
от среднего
на две части объяснен. и необъяснен.
Известно что
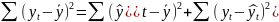
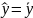 .
Тогда
вся дисперсия результативного
признака обусловлена воздействием
прочих факторов и общая сумма квадратов
отклонений совпадет с остаточной.
Если же прочие факторы не влияют на
результат,
то
связан
с
функционально
и остаточная сумма квадратов равна
нулю. Тогда сумма квадратов отклонений,
объясненная регрессией, совпадает с
общей
суммой квадратов.
.
Тогда
вся дисперсия результативного
признака обусловлена воздействием
прочих факторов и общая сумма квадратов
отклонений совпадет с остаточной.
Если же прочие факторы не влияют на
результат,
то
связан
с
функционально
и остаточная сумма квадратов равна
нулю. Тогда сумма квадратов отклонений,
объясненная регрессией, совпадает с
общей
суммой квадратов.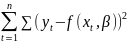 ,
,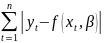
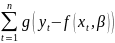 ,
где g—
«мера», с которой отклонение
,
где g—
«мера», с которой отклонение
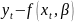 входит
в функционал F
входит
в функционал F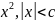

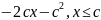
 используются теоретические (расчетные)
значения результативного признака
.
Для линейной регрессии
используются теоретические (расчетные)
значения результативного признака
.
Для линейной регрессии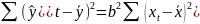 .
(1)
Это
следует из формулы линейного
коэффициента корреляции , из которой
получим
.
(1)
Это
следует из формулы линейного
коэффициента корреляции , из которой
получим
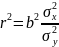 ,
где
,
где
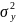 общая
дисперсия признака у.
Получаем, что
общая
дисперсия признака у.
Получаем, что
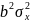 дисперсия признака
,
обусловленная
фактором
.
И соответ.
запишется как (1), т.к. объясненн. Сумма
квадрат. при линейн. регрессии зависит
только от одной константы-коэффициента
регрессии
,
то данная сумма квадрат. имеет одну
степень свободы(
дисперсия признака
,
обусловленная
фактором
.
И соответ.
запишется как (1), т.к. объясненн. Сумма
квадрат. при линейн. регрессии зависит
только от одной константы-коэффициента
регрессии
,
то данная сумма квадрат. имеет одну
степень свободы(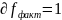 ).
).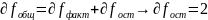 .
.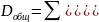 ,
,
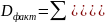 ,
,
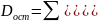 .
Отношение
факторную и
остаточную дисперсии на одну степень
свободы, получим величину F-отношения
(F-критерий):
.
Отношение
факторную и
остаточную дисперсии на одну степень
свободы, получим величину F-отношения
(F-критерий):

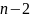 .
Если полученная в результате числовой
обработки
результатов эксперимента Fфакт
> Fтабл
то гипотеза Н0
отклоняется.(принимается
.
Если полученная в результате числовой
обработки
результатов эксперимента Fфакт
> Fтабл
то гипотеза Н0
отклоняется.(принимается
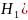 и регрессия считается значимой . В
противном случае уравнение регрессии
считается статистически незначимым,
т.е. коэффициент регрессии
можно заменить нулём.
и регрессия считается значимой . В
противном случае уравнение регрессии
считается статистически незначимым,
т.е. коэффициент регрессии
можно заменить нулём. ,а
остаточную сумму квадратов
,а
остаточную сумму квадратов
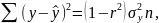 тогда значение F-критерия
можно выразить как
тогда значение F-критерия
можно выразить как

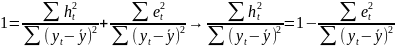 (6)
(6)
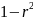 характеризует
долю дисперсии
,
вызванную
влиянием остальных, не учтенных
признаков.
характеризует
долю дисперсии
,
вызванную
влиянием остальных, не учтенных
признаков.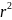 . Коэффициент
корреляции ,
-описывает
«степень плотности» экспериментальных
точек вокруг линии регрессии,
. Коэффициент
корреляции ,
-описывает
«степень плотности» экспериментальных
точек вокруг линии регрессии,
 задает долю объясненной дисперсии в
общей дисперсии результирующего
фактора.
задает долю объясненной дисперсии в
общей дисперсии результирующего
фактора.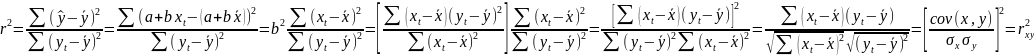
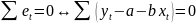 и
и (1)
(1)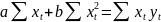 )
очевидно, что решения системы явл (
)
очевидно, что решения системы явл ( (3),
)
(3),
)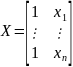 ,
,
 ,
,
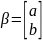 ,
,
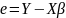 .
Условие ортогон.(1) запишем матричным
уравнением :
.
Условие ортогон.(1) запишем матричным
уравнением :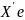 =0
или
=0
или
 ,
получаем
,
получаем
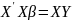 решением кот. явл.
решением кот. явл.
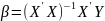 (2),
т.к.
предполаг., что
(2),
т.к.
предполаг., что
 ЛНЗ, то матр.
ЛНЗ, то матр.
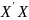 обратима..
обратима..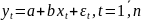 –.
–.
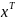 не коллинеар. един.вектору
не коллинеар. един.вектору
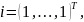 т.е. не все
т.е. не все
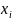 одинаковы.
одинаковы. ,
3б.
,
3б.
 – не зависит от
.
– не зависит от
.
 – некоррелированность ошибок для
различных наблюдений.
– некоррелированность ошибок для
различных наблюдений.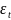 имеют
совместное нормальное распределение
имеют
совместное нормальное распределение
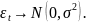
 при t ≠ s.
при t ≠ s.
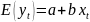 ,
т.е. при фиксированном
регрессия указывает на среднее
ожидаемое значение
,
т.е. при фиксированном
регрессия указывает на среднее
ожидаемое значение
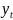 .
.
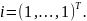 3.
,
– не зависит от
.
4.
3.
,
– не зависит от
.
4.
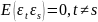
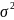 .
Термин «наилучший» в данном случае
означ. найти в классе лин. несмещ.
оценок наилучшую в смысле мин. дисперсии
(BLUE).
.
Термин «наилучший» в данном случае
означ. найти в классе лин. несмещ.
оценок наилучшую в смысле мин. дисперсии
(BLUE).
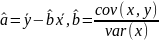 ,
получ.
с испол-нием МНК, имеют наим. дисперсию
в классе всех лин. несмещ. оценок.
,
получ.
с испол-нием МНК, имеют наим. дисперсию
в классе всех лин. несмещ. оценок.
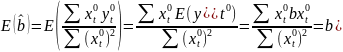 ,
,
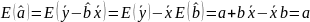
 :
: в виде:
в виде:
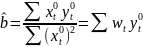 ,
где
,
где
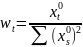 ,
причём 1)
,
причём 1)
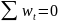 ,
2)
,
2)
 ,
3)
,
3) ,
4)
,
4)
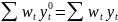 ,
тогда
,
тогда
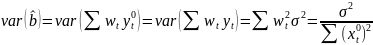 .
.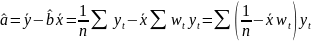 ,
тогда
,
тогда
 прогнозное знач.
в точке
.
Остатки
регрессии
прогнозное знач.
в точке
.
Остатки
регрессии
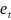 определяются
из уравнения
определяются
из уравнения
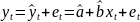 .
(Надо различать остатки регрессии и
ошибки регрессии
.
Остатки в отличие от ошибок наблюдаемы.)
.
(Надо различать остатки регрессии и
ошибки регрессии
.
Остатки в отличие от ошибок наблюдаемы.)
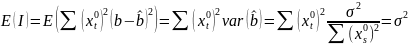
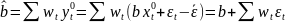 ,
получаем
,
получаем
 ,
,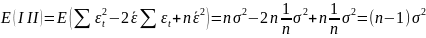 .
.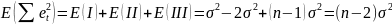 ,откуда
следует, что
,откуда
следует, что
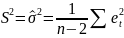 (1)является
несмещ. оценкой дисперсии ошибок
(1)является
несмещ. оценкой дисперсии ошибок
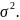
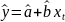 (
получены
на основе оценки выборки)
обычно оценивается значимость не
только уравнения в целом, но и отдельных
его пар-ров. С этой целью по каждому
из пар-ров определяется его станд.
ошибка:
(
получены
на основе оценки выборки)
обычно оценивается значимость не
только уравнения в целом, но и отдельных
его пар-ров. С этой целью по каждому
из пар-ров определяется его станд.
ошибка: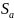 и
и
 .
.
 ,
где
,
где
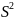 – остаточная дисперсия на одну степень
свободы.
– остаточная дисперсия на одну степень
свободы.
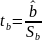 ),
кот.подчиняется стат-ке Стьюдента с
(n – 2) степенями свободы. Эта статистика
применяется для проверки статистической
значимости коэффициента регрессии
и для расчёта его доверительных
интервалов.
),
кот.подчиняется стат-ке Стьюдента с
(n – 2) степенями свободы. Эта статистика
применяется для проверки статистической
значимости коэффициента регрессии
и для расчёта его доверительных
интервалов.
 сравнивают с критическим значением
сравнивают с критическим значением
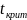 с заданным уровнем значимости α и
ко-вом степеней свободы (n – 2).
с заданным уровнем значимости α и
ко-вом степеней свободы (n – 2).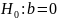 – осн. гипотеза, и ей альтернативная
:
– осн. гипотеза, и ей альтернативная
: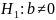 .
.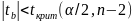 ,
то приним-ся нулевая гипотеза и пар-р
bсчит.
не значимым (т.е. его можно заменить
0). Если
,
то приним-ся нулевая гипотеза и пар-р
bсчит.
не значимым (т.е. его можно заменить
0). Если
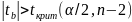 ,
то гип.
отвергается и пар-р bявл.
значимым.
,
то гип.
отвергается и пар-р bявл.
значимым. в уравнение регрессии
в уравнение регрессии
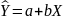 .
Но данный точечный прогноз не всегда
реален. Он должен дополняться расчетом
стандартной ошибки
.
Но данный точечный прогноз не всегда
реален. Он должен дополняться расчетом
стандартной ошибки
 и соответственно интервальной оценкой
прогноза значения результата Y*. Т.е.
Y*∈[
и соответственно интервальной оценкой
прогноза значения результата Y*. Т.е.
Y*∈[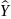 −
;
+
].
Получим данную оценку. Для линейной
регрессии
−
;
+
].
Получим данную оценку. Для линейной
регрессии
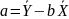 . Подставим
. Подставим
 =
=
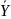 +
b(X
−
+
b(X
−
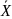 ) .Отсюда следует, что стандартная
ошибка
зависит от ошибки
и ошибки коэффициента b, т.е.
) .Отсюда следует, что стандартная
ошибка
зависит от ошибки
и ошибки коэффициента b, т.е.
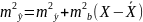 Из
математической статистики известно,
что
Из
математической статистики известно,
что
 .
Возьмем в качестве оценки
.
Возьмем в качестве оценки
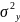 остаточную дисперсию на одну степень
свободы
,
получим
остаточную дисперсию на одну степень
свободы
,
получим
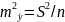 ;
;
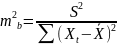 ;
Считая, что прогнозное значение равно
получим следующую формулу расчета
квадрата стандартной ошибки предсказания
;
Считая, что прогнозное значение равно
получим следующую формулу расчета
квадрата стандартной ошибки предсказания
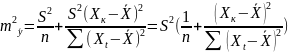 .
Откуда
.
Откуда
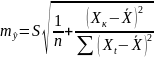
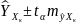 .
. -
гипербола;2)
-
гипербола;2) -полиномиальная;3)
-полиномиальная;3)
 -
обратная;4)
-
обратная;4) -
полулогарифмическая; 5)
-
полулогарифмическая; 5)
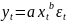 – степенная; 6)
– степенная; 6)
 – показательная; 7)
– показательная; 7)
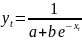 – логическая.
– логическая.
 ,
где
,
где
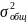 — общая дисперсия результат.признака
у;
— общая дисперсия результат.признака
у;
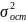 — остат. дисперсия. Т.к.
— остат. дисперсия. Т.к.
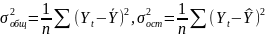 ,
то индекс корреляции можно выразить
как:
,
то индекс корреляции можно выразить
как:
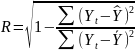 .
Величина данного показателя находится
в границах: 0 < R < 1, чем
ближе к единице, тем теснее связь
рассматриваемых признаков, тем более
надежно найденное уравнение регрессии.
Если нелин. относительно объясн.
переменной уравнение регрессии при
линеаризации принимает форму линейного
уравнения парной регрессии, то для
оценки тесноты связи может быть
использован линейный коэффициент
корреляции, вел-на кот.в этом случае
совпадет с индексом корреляции.
.
Величина данного показателя находится
в границах: 0 < R < 1, чем
ближе к единице, тем теснее связь
рассматриваемых признаков, тем более
надежно найденное уравнение регрессии.
Если нелин. относительно объясн.
переменной уравнение регрессии при
линеаризации принимает форму линейного
уравнения парной регрессии, то для
оценки тесноты связи может быть
использован линейный коэффициент
корреляции, вел-на кот.в этом случае
совпадет с индексом корреляции.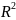 имеет тот же смысл, что и коэффициент
детерм. В специальных исследованияхвел-ну
для нелин. связей наз. индексом
детерминации. Оценка существенности
индекса корреляции проводится, так
же как и оценка надежности коэффициента
корреляции. Индекс детерминации
используется для проверки существенности
в целом уравнения нелинейной регрессии
по F-критерию Фишера:
имеет тот же смысл, что и коэффициент
детерм. В специальных исследованияхвел-ну
для нелин. связей наз. индексом
детерминации. Оценка существенности
индекса корреляции проводится, так
же как и оценка надежности коэффициента
корреляции. Индекс детерминации
используется для проверки существенности
в целом уравнения нелинейной регрессии
по F-критерию Фишера:
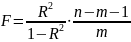 ,
где
—
индекс детерминации; n — число
наблюдений; m — число параметров при
пер. х.
,
где
—
индекс детерминации; n — число
наблюдений; m — число параметров при
пер. х.
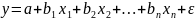
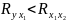 для
зависимости у = а +
для
зависимости у = а +
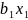 +
+
 +ε может привести к нежелательным
последствиям — система уравнений
может оказаться плохо обусловленной
и повлечь за собой неустойчивость и
ненадежность оценок коэффициентов
регрессии. Если между факторами
существует высокая корреляция, то
нельзя определить их изолированное
влияние на результативный показатель
и параметры уравнения регрессии
оказываются неинтерпретируемыми.
+ε может привести к нежелательным
последствиям — система уравнений
может оказаться плохо обусловленной
и повлечь за собой неустойчивость и
ненадежность оценок коэффициентов
регрессии. Если между факторами
существует высокая корреляция, то
нельзя определить их изолированное
влияние на результативный показатель
и параметры уравнения регрессии
оказываются неинтерпретируемыми. :
: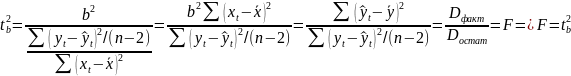 или
значим.(незначим.) регрессии в целом
совпадает со значим. (незначим.) пар.
b.
или
значим.(незначим.) регрессии в целом
совпадает со значим. (незначим.) пар.
b.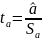 ,
где
,
где
 .
Процедура оценивания значимости
данного пар-ра аналогична процедуре
оценивания пар. b.
.
Процедура оценивания значимости
данного пар-ра аналогична процедуре
оценивания пар. b.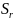 :
:
 .
.
 ,
возведём в квадрат:
,
возведём в квадрат:
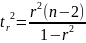 .
.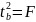 можно утверждать, что для случ. Пар.лин.
регрессии совпад. Пок-ли значимости
регрессии в целом, коэф. регрессии и
коэф. лин. корреляции r.
можно утверждать, что для случ. Пар.лин.
регрессии совпад. Пок-ли значимости
регрессии в целом, коэф. регрессии и
коэф. лин. корреляции r.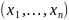 .
Необходимо выбрать
так, чтобы точность оценки коэффиц.
была наибол.Из формулы
.
Необходимо выбрать
так, чтобы точность оценки коэффиц.
была наибол.Из формулы
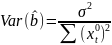 видно, что чем больше
видно, что чем больше
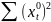 ,
тем меньше дисперсия
,
тем меньше дисперсия
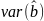 .
Поэтому желательно выбирать
таким образом, чтобы их разброс вокруг
среднего был большим.
.
Поэтому желательно выбирать
таким образом, чтобы их разброс вокруг
среднего был большим.

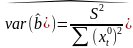 ,
,
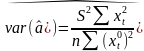 ,
,
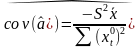 ,
где
вычисляется по формуле (1).
,
где
вычисляется по формуле (1).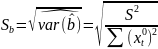 .
. .
.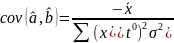 . (1)
. (1) ,
если
,
если
 .
График регрессии всегда проходит
через точку с координатами
,
поэтому при увелич.
–
aˆ уменьш..
.
График регрессии всегда проходит
через точку с координатами
,
поэтому при увелич.
–
aˆ уменьш..
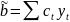 —
любая другая несмещ. оценка. Представим
—
любая другая несмещ. оценка. Представим
 в виде
в виде
 ,
тогда
,
тогда
 ,
следоват.
,
следоват.
 .
.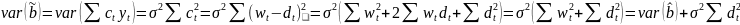 ,
т.е.
,
т.е.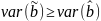 ,
Аналогичные вычисления показывают,
что
,
Аналогичные вычисления показывают,
что
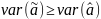 .ч.т.д.
.ч.т.д.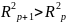 и
и
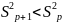 .
Если же этого не происходит и данные
показатели практически мало отличаются
друг от друга, то включаемый в анализ
фактор
.
Если же этого не происходит и данные
показатели практически мало отличаются
друг от друга, то включаемый в анализ
фактор
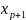 не улучшает модель и практически
является лишним фактором.
не улучшает модель и практически
является лишним фактором.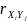 ≥ 0,7
≥ 0,7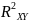 можно сравнивать с коэф.детерм.
можно сравнивать с коэф.детерм. для обоснования возможности применения
лин. ф-ции. Чем больше кривизна линии
регрессии тем величина коэффициента
детерминации
меньшеиндекса детерм.
.
Близость этих показателей означает,
что нет необх-ти усложнять форму
ур-ния регрессии и можно исп-тьлин.
ф-цию. Практически если в-на (
–
) не превышает 0,1, то предпол-ние о лин.
форме связи считается оправданным.
В противном случае проводится оценка
сущ-ти различия, вычисленных по одним
и тем же исходным данным, через t-кр.
Стьюдента:
для обоснования возможности применения
лин. ф-ции. Чем больше кривизна линии
регрессии тем величина коэффициента
детерминации
меньшеиндекса детерм.
.
Близость этих показателей означает,
что нет необх-ти усложнять форму
ур-ния регрессии и можно исп-тьлин.
ф-цию. Практически если в-на (
–
) не превышает 0,1, то предпол-ние о лин.
форме связи считается оправданным.
В противном случае проводится оценка
сущ-ти различия, вычисленных по одним
и тем же исходным данным, через t-кр.
Стьюдента: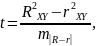 где
где
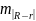 — ошибка разн., опр-мая по фо-ле:
— ошибка разн., опр-мая по фо-ле:
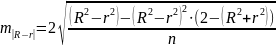 Если
Если
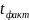 >
> то различия между рассматриваемыми
показателями корреляции существенны
и замена нелинейной регрессииуравнениемлинейной
функции невозможна. Практически если
вел-на t < 2 , то различия между
то различия между рассматриваемыми
показателями корреляции существенны
и замена нелинейной регрессииуравнениемлинейной
функции невозможна. Практически если
вел-на t < 2 , то различия между
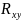 и
несущ.,
и, след., возможно прим.лин. регрессии,
даже если есть предп-нияо некоторой
нелин.рассм-емыхсоотн-ний признаков
фактора и рез-та.
и
несущ.,
и, след., возможно прим.лин. регрессии,
даже если есть предп-нияо некоторой
нелин.рассм-емыхсоотн-ний признаков
фактора и рез-та.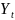 и
и
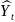 .
Чем меньше это отличие, тем ближе
теор-кие значения подходят к эмпир-ким
данным, лучше кач-во модели. Вел-на
откл. фактических и расчетных значений
резул-ного признака (
.
Чем меньше это отличие, тем ближе
теор-кие значения подходят к эмпир-ким
данным, лучше кач-во модели. Вел-на
откл. фактических и расчетных значений
резул-ного признака (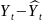 )
по каждому набл-июпредставл. собой
ошибку аппроксимации. Их число
соответствует объему сов-ти. В отдельных
случаях ошибка аппр-ции может оказаться
равной 0. Отклонения (
)
несравнимы между собой, исключая
вел-ну, равную0. Поскольку (
)
может быть как величиной полож., так
и отриц., то ошибки аппр-ции для каждого
наблюдения принято определять в
процентах по модулю. Откл. (
)
можно рассматривать как абс. ошибку
аппроксимации, а
)
по каждому набл-июпредставл. собой
ошибку аппроксимации. Их число
соответствует объему сов-ти. В отдельных
случаях ошибка аппр-ции может оказаться
равной 0. Отклонения (
)
несравнимы между собой, исключая
вел-ну, равную0. Поскольку (
)
может быть как величиной полож., так
и отриц., то ошибки аппр-ции для каждого
наблюдения принято определять в
процентах по модулю. Откл. (
)
можно рассматривать как абс. ошибку
аппроксимации, а
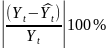 как
относ.ошибку аппроксимации. Чтобы
иметь общее суждение о качестве модели
из относ.отклонений по каждому
набл-нию, опред.Ср. ошибку аппроксимации
как среднюю арифм. простую:
как
относ.ошибку аппроксимации. Чтобы
иметь общее суждение о качестве модели
из относ.отклонений по каждому
набл-нию, опред.Ср. ошибку аппроксимации
как среднюю арифм. простую:
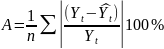
 .
Параметр b в ней имеет четкое
экономическое истолкование —
коэффициент эластичности. Величина
параметра b показывает на сколько
процентов в среднем изменяется
результат при изменении фактора на
1%.
.
Параметр b в ней имеет четкое
экономическое истолкование —
коэффициент эластичности. Величина
параметра b показывает на сколько
процентов в среднем изменяется
результат при изменении фактора на
1%.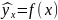 формуле
формуле
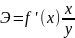 .
Только для степеннойфункции коэффициент
эластичности — величина постоянная.
Для других функций коэффициент
эластичности зависит от значений
фактора х. Поэтому обычно рассчитывают
средний показатель эластичности. Для
линейной регрессии он может быть
выражен как
.
Только для степеннойфункции коэффициент
эластичности — величина постоянная.
Для других функций коэффициент
эластичности зависит от значений
фактора х. Поэтому обычно рассчитывают
средний показатель эластичности. Для
линейной регрессии он может быть
выражен как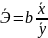 .
.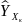 представляют собой гиперболы,
расположенные по обе стороны от линии
регрессии. Фактические значения Y
варьируют около среднего значения
на величину случайной ошибки ε,
дисперсия которой оценивается как
остаточная дисперсия на одну степень
свободы
.
Поэтому ошибка предсказываемого
индивидуального значения Y должна
включать не только стандартную ошибку
представляют собой гиперболы,
расположенные по обе стороны от линии
регрессии. Фактические значения Y
варьируют около среднего значения
на величину случайной ошибки ε,
дисперсия которой оценивается как
остаточная дисперсия на одну степень
свободы
.
Поэтому ошибка предсказываемого
индивидуального значения Y должна
включать не только стандартную ошибку
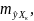 но
и случайную ошибку S. Средняя ошибка
прогнозируемого индивидуального
значения у
составит:
но
и случайную ошибку S. Средняя ошибка
прогнозируемого индивидуального
значения у
составит:

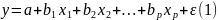

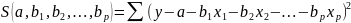
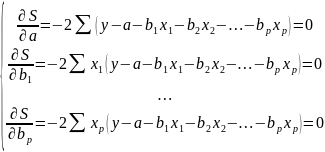
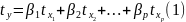
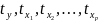 –стандартизир.пер-ные
–стандартизир.пер-ные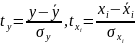 ,для
кот.ср. значение равно0, а дисперсия
равна 1.
,для
кот.ср. значение равно0, а дисперсия
равна 1.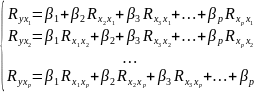
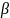 -
стандартизированные коэффициенты
регрессии (
-коэффициенты). Стандартизированные
коэффициенты регрессии показывают,
на сколько “сигм” изменится в среднем
результат, если соответствующий
фактор
изменится на 1 сигму при низменном
уровне других факторов. Поскольку
все переменные центрированные,
нормированные и безразмерные,
стандартизованные коэффициенты
регрессии
-
стандартизированные коэффициенты
регрессии (
-коэффициенты). Стандартизированные
коэффициенты регрессии показывают,
на сколько “сигм” изменится в среднем
результат, если соответствующий
фактор
изменится на 1 сигму при низменном
уровне других факторов. Поскольку
все переменные центрированные,
нормированные и безразмерные,
стандартизованные коэффициенты
регрессии
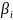 сравнимы
между собой. Сравнивая их друг с
другом, можно ранжировать факторы по
силе их воздействия
на результат. В этом основное достоинство
стандартизированных коэффициентов
регрессии в отличие от коэффициентов
«чистой» регрессии.
сравнимы
между собой. Сравнивая их друг с
другом, можно ранжировать факторы по
силе их воздействия
на результат. В этом основное достоинство
стандартизированных коэффициентов
регрессии в отличие от коэффициентов
«чистой» регрессии.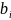 и
стандартизированными коэффициентами
регрессии
.
и
стандартизированными коэффициентами
регрессии
.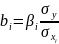
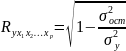

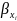 -
стандартизованные коэффициенты
регрессии;
-
стандартизованные коэффициенты
регрессии;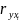 -
парные
коэффициенты корреляции результата
с каждым фактором.
-
парные
коэффициенты корреляции результата
с каждым фактором.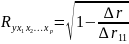
 - определитель матрицы парных
коэффициентов корреляции;
- определитель матрицы парных
коэффициентов корреляции; - определитель матрицы межфакторной
корреляции.
- определитель матрицы межфакторной
корреляции.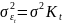 ,
,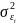 -
дисперсия ошибки при конкретном t-м
знач. фактора;
-постоянная
дисперсия ошибки при соблюдении
предпосылки о гомоск. остатков;
Кt–коэф-т
пропорц-ти, меняющийся с изменением
величины фактора.
-
дисперсия ошибки при конкретном t-м
знач. фактора;
-постоянная
дисперсия ошибки при соблюдении
предпосылки о гомоск. остатков;
Кt–коэф-т
пропорц-ти, меняющийся с изменением
величины фактора.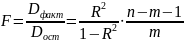 где
Dфакт
- факторная сумма квадратов на одну
степень свободы; Dост
- остаточная сумма квадратов на одну
степень свободы; R2
-индекс множественной детерминации;
m -число параметров при переменных х;
п - число наблюдений.
где
Dфакт
- факторная сумма квадратов на одну
степень свободы; Dост
- остаточная сумма квадратов на одну
степень свободы; R2
-индекс множественной детерминации;
m -число параметров при переменных х;
п - число наблюдений. ,
где
,
где
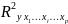 -
коэффициент множественной детерминации
для модели с полным набором факторов;
-
коэффициент множественной детерминации
для модели с полным набором факторов;
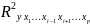 - тот же показатель, но без включения
в модель фактора xi;
- тот же показатель, но без включения
в модель фактора xi;
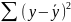 или, что то же самое, на nσ2y,
то получим соотношение приростафакторной
суммыквадратов отклонений к остаточной
сумме квадратов.
или, что то же самое, на nσ2y,
то получим соотношение приростафакторной
суммыквадратов отклонений к остаточной
сумме квадратов.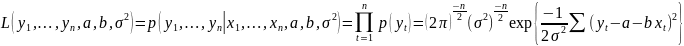 ,
где
р
обозначает плотность вер-ти, завис.
от xt,yt
и параметров а, b, σ2
.
,
где
р
обозначает плотность вер-ти, завис.
от xt,yt
и параметров а, b, σ2
.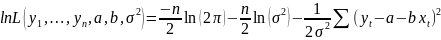


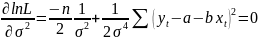
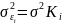 модель
примет вид
модель
примет вид .
. .
Тогда
дисперсия остатков будет постоянной,
т.е.
.
Тогда
дисперсия остатков будет постоянной,
т.е.
 .
Уравнение
регрессии примет вид:
.
Уравнение
регрессии примет вид:
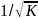 .
.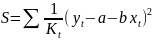
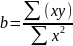 ,
в этом случае эта формула примет вид
,
в этом случае эта формула примет вид
 ,
,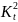 .Kt-
представляет
собой коэффициент пропорц-ти, приним.
различные
значения для соответствующих t-х
значений
факторов х1и
х2.
Ввиду
того, что
рассматриваемая
модель примет вид
.Kt-
представляет
собой коэффициент пропорц-ти, приним.
различные
значения для соответствующих t-х
значений
факторов х1и
х2.
Ввиду
того, что
рассматриваемая
модель примет вид
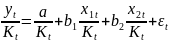
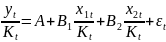
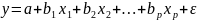 определ.
матрицы коэф-тов парной корреляции
примет вид:
определ.
матрицы коэф-тов парной корреляции
примет вид: Определитель
более низкого порядка
получается, когда вычеркиваются
из матрицы коэффициентов парной
корреляции первый столбец и первая
строка,
что и соответствует матрице коэф-тов
парной корреляции между факторами:
Определитель
более низкого порядка
получается, когда вычеркиваются
из матрицы коэффициентов парной
корреляции первый столбец и первая
строка,
что и соответствует матрице коэф-тов
парной корреляции между факторами: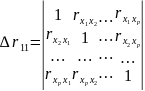
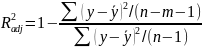 ,
где
m
- число
параметров при пер-ных; п
- число
наблюдений,
,
где
m
- число
параметров при пер-ных; п
- число
наблюдений,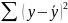 остаточная сумма квадратов,
остаточная сумма квадратов,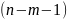 число степеней свободы остаточной
вариации,
общая
сумма квадратов отклонений,
число степеней свободы остаточной
вариации,
общая
сумма квадратов отклонений, число степеней свободы в целом по
совокупности.
число степеней свободы в целом по
совокупности.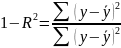 ,
то величину скоррект. индекса детерм.
можно представить в виде
,
то величину скоррект. индекса детерм.
можно представить в виде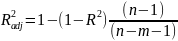



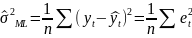

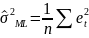 явл.смещенной,
носостоят.оценкой σ2
явл.смещенной,
носостоят.оценкой σ2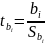 где
bi
- коэффициент
чистой регрессии при факторе хi;Sbi-
средняя
квадратич. ошибка коэффициента
регрессии bi.
где
bi
- коэффициент
чистой регрессии при факторе хi;Sbi-
средняя
квадратич. ошибка коэффициента
регрессии bi. средняя
квадрат.ошибка коэффициента регрессии
м.б. определена по формуле:
средняя
квадрат.ошибка коэффициента регрессии
м.б. определена по формуле: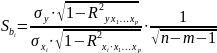 ,
где
,
где
 –коэф.
детерминации для завис-ти ф.xi
со всемидр. факт-ми ур-ниямнож.
регрессии.
–коэф.
детерминации для завис-ти ф.xi
со всемидр. факт-ми ур-ниямнож.
регрессии.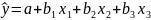 для
оценки знач.коэф. регрессии b1,
b2,
b3
необходим
расчёт 3 межфакт. коэф. детерминации
для
оценки знач.коэф. регрессии b1,
b2,
b3
необходим
расчёт 3 межфакт. коэф. детерминации
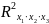 ,
,
 ,
,
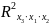 .
.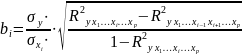 ,то можно убедиться, что
,то можно убедиться, что

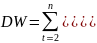 .
.

 Т.е.
если в остатках сущ.полнаяполож.автокор.,
то
Т.е.
если в остатках сущ.полнаяполож.автокор.,
то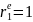 ,
а DW=0,
,
а DW=0,
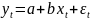 (1)
(1)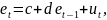 где с и d
— пар-рыур-ния регрессии.
где с и d
— пар-рыур-ния регрессии.
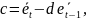
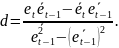
 (коэф.
автокорреляции остатков 1 порядка).
(коэф.
автокорреляции остатков 1 порядка).
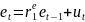 (
(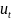 -случ.
ошибка без автокор-ции). Ур-ниерегрес.
(1) можно переписать:
-случ.
ошибка без автокор-ции). Ур-ниерегрес.
(1) можно переписать:
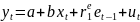 .
.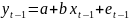 .
.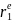 :
:
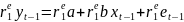 .
.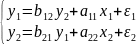
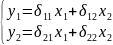
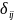 коэффициенты
приведенной формы модели
(ПК).
коэффициенты
приведенной формы модели
(ПК).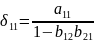 ,
,
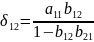 ,
,
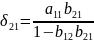 ,
,
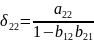
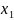 после исключ. влияния
после исключ. влияния
 .
.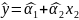
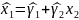
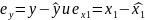 .
.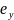 и
и
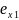 :
:
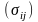 .
.
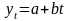
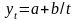
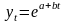

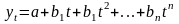
 а в качестве зависимой переменной –
фактические уровни временного ряда
а в качестве зависимой переменной –
фактические уровни временного ряда
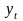 .
Для
нелинейных трендов предварительно
проводят стандартную процедуру их
линеаризации.
.
Для
нелинейных трендов предварительно
проводят стандартную процедуру их
линеаризации.


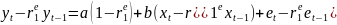 или
или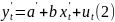 .
.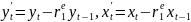
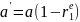 как
как
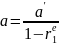 .
.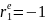 ,
т.е. в остатках наблюдается полная
отр. автокорреляция, то изложенный
выше метод модифицируется след.образом:
,
т.е. в остатках наблюдается полная
отр. автокорреляция, то изложенный
выше метод модифицируется след.образом:
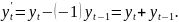
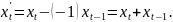
 ,имеем:
,имеем: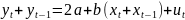 .
.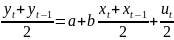 (3).
(3). .
.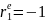 ,
DW=4.
Если автокорреляция остатков
отсутствует, то
,
DW=4.
Если автокорреляция остатков
отсутствует, то
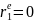 ,
DW=2.
Следовательно,
,
DW=2.
Следовательно,
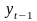 тесно
коррелируют. В этом случае коэффициент
автокорреляции первого порядка
уровней исходного ряда должен быть
высоким. Если временной ряд содержит
нелинейную тенденцию, например, в
форме экспоненты, то коэффициент
автокорреляции первого порядка по
логарифмам уровней исходного ряда
будет выше, чем соответствующий
коэффициент, рассчитанный по уровням
ряда. Чем сильнее выражена нелинейная
тенденция в изучаемом временном ряде,
тем в большей степени будут различаться
значения указанных коэффициентов.
тесно
коррелируют. В этом случае коэффициент
автокорреляции первого порядка
уровней исходного ряда должен быть
высоким. Если временной ряд содержит
нелинейную тенденцию, например, в
форме экспоненты, то коэффициент
автокорреляции первого порядка по
логарифмам уровней исходного ряда
будет выше, чем соответствующий
коэффициент, рассчитанный по уровням
ряда. Чем сильнее выражена нелинейная
тенденция в изучаемом временном ряде,
тем в большей степени будут различаться
значения указанных коэффициентов.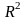 и выбора
уравнения тренда с максимальным
значением скорректированного
коэффициента детерминации.
и выбора
уравнения тренда с максимальным
значением скорректированного
коэффициента детерминации. и
х
=
и
х
=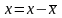 .
Тогда система примет вид
.
Тогда система примет вид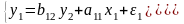 (1)Получим
приведенную форму модели
(1)Получим
приведенную форму модели
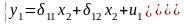 (2),
где
(2),
где
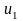 и
и
 случайные
ошибки приведенной формы модели. Для
каждого уравнения приведенной формы
модели применим традиционный МНК.
Переходим к структурной форме модели
(1). Для этого из первого уравнения
приведенной формы (2) исключаем
случайные
ошибки приведенной формы модели. Для
каждого уравнения приведенной формы
модели применим традиционный МНК.
Переходим к структурной форме модели
(1). Для этого из первого уравнения
приведенной формы (2) исключаем ,
выразив его из второго уравнения и
подставив в первое После преобразований
получим
,
выразив его из второго уравнения и
подставив в первое После преобразований
получим
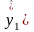 .
Чтобы найти второе уравнение структурной
модели из первого уравнения приведенной
формы выразим
.
Чтобы найти второе уравнение структурной
модели из первого уравнения приведенной
формы выразим
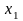 ,
Откуда получим второе уравнение
структурной формы модели
,
Откуда получим второе уравнение
структурной формы модели
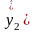 .
Свободные члены уравнений определим
по формулам:
.
Свободные члены уравнений определим
по формулам:
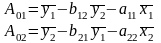 Оценка
значимости модели дается черезF-критерий
и
Оценка
значимости модели дается черезF-критерий
и
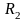 для каждого уравнения в отдельности.
При сравнении результатов, полученных
традиционным МНК и с помощью КМНК,
следует иметь в виду, что традиционный
МНК, применяемый к каждому уравнению
структурной формы модели, взятому в
отдельности, дает смещенные оценки
структурных коэффициентов. Кроме
того, при интерпретации коэффициентов
множественной регрессии предполагается
независимость факторов друг от друга,
что становится невозможным при
рассмотрении системы совместных
уравнений.
для каждого уравнения в отдельности.
При сравнении результатов, полученных
традиционным МНК и с помощью КМНК,
следует иметь в виду, что традиционный
МНК, применяемый к каждому уравнению
структурной формы модели, взятому в
отдельности, дает смещенные оценки
структурных коэффициентов. Кроме
того, при интерпретации коэффициентов
множественной регрессии предполагается
независимость факторов друг от друга,
что становится невозможным при
рассмотрении системы совместных
уравнений.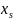 ,
удаление которого приводит к наименьшему
уменьшению коэффициента детерминации.
Затем сравнивается значение F-статистики
для проверки гипотезы
о незначимости этого регрессора с
некоторым заранее заданным пороговым
значением
,
удаление которого приводит к наименьшему
уменьшению коэффициента детерминации.
Затем сравнивается значение F-статистики
для проверки гипотезы
о незначимости этого регрессора с
некоторым заранее заданным пороговым
значением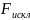 .
Если
.
Если
 ,
то
удаляется
из списка регрессоров. Заметим, что
гипотеза
о равенстве коэффициента
при
нулю
эквивалентна гипотезе о равенстве
коэффициентов детерминации
до и после удаления регрессора, а
также гипотезе о том, что коэффициент
частной корреляции
и
равен
0.
,
то
удаляется
из списка регрессоров. Заметим, что
гипотеза
о равенстве коэффициента
при
нулю
эквивалентна гипотезе о равенстве
коэффициентов детерминации
до и после удаления регрессора, а
также гипотезе о том, что коэффициент
частной корреляции
и
равен
0.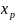 с
наибольшим по модулю частным
коэффициентом корреляции (исключается
влияние ранее включенных в уравнение
регрессоров) и сравниваем значение
F-статистики
для проверки гипотезы
о незначимости этого регрессора с
некоторым
заранее заданным пороговым значением
с
наибольшим по модулю частным
коэффициентом корреляции (исключается
влияние ранее включенных в уравнение
регрессоров) и сравниваем значение
F-статистики
для проверки гипотезы
о незначимости этого регрессора с
некоторым
заранее заданным пороговым значением
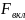 .
Если
.
Если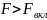 ,
то
включается в список регрессоров.
Обычно выбирают
,
то
включается в список регрессоров.
Обычно выбирают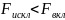 .
Второй шаг повторяется до тех пор,
пока происходит изменение списка
регрессоров. Конечно, ни одна из
пошаговых процедур не гарантирует
получение оптимального по какому-либо
критерию набора регрессоров.
.
Второй шаг повторяется до тех пор,
пока происходит изменение списка
регрессоров. Конечно, ни одна из
пошаговых процедур не гарантирует
получение оптимального по какому-либо
критерию набора регрессоров.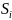
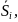 В
моделях с сезонной компонентой обычно
предполагается, что сезонные воздействия
за период взаимопогашаются. В аддит.
модели это выражается в том, что сумма
значений сез.комп. по всем кварталам
должна быть равна 0.
В
моделях с сезонной компонентой обычно
предполагается, что сезонные воздействия
за период взаимопогашаются. В аддит.
модели это выражается в том, что сумма
значений сез.комп. по всем кварталам
должна быть равна 0.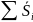 /4.
/4.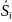 -
к, где i=
-
к, где i=
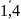
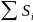 .
.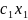 +…+
+…+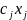 +…+
+…+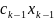 +
+
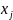 ={
1,для
каждого j
внутри цикла, 0, во всех остал.cлучаях}
={
1,для
каждого j
внутри цикла, 0, во всех остал.cлучаях}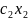 +
+ +
(1)
+
(1)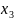 ={
1,для третьего квартала
={
1,для третьего квартала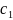 +
;
+
;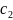 ,+
;
,+
;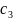 +
;
+
;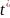 и после момента
)
и построить отдельно по каждой подсов.
ур-ниялин. регрессии (на рисунке -
прямые (1) и (2)). Если структурные
изменения незначительно повлияли на
характер тенденции ряда
,
то ее можно описать с помощью единого
для всей сов-ти данных ур-ния тренда
(на рисунке - прямая (3)).
и после момента
)
и построить отдельно по каждой подсов.
ур-ниялин. регрессии (на рисунке -
прямые (1) и (2)). Если структурные
изменения незначительно повлияли на
характер тенденции ряда
,
то ее можно описать с помощью единого
для всей сов-ти данных ур-ния тренда
(на рисунке - прямая (3)).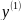 =
=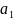 +
+ *t
*t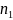
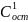

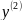 =
= +
+ *t
*t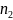
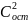
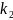
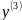 =
=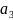 +
+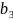 *t
*t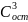
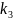
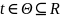 (вещ.числа)
наз. стохастическим
процессом.Дискр.
стох. процесс определяется
как последовательность случ. переменных
X(t),
где
t
= t1,
t2,
...,
tT,
кот.будем обозначать Х1,
Х2,...,
ХТ...,
или
просто Xt.
(вещ.числа)
наз. стохастическим
процессом.Дискр.
стох. процесс определяется
как последовательность случ. переменных
X(t),
где
t
= t1,
t2,
...,
tT,
кот.будем обозначать Х1,
Х2,...,
ХТ...,
или
просто Xt. .
.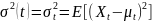 .
.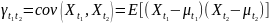
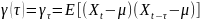
 для t1≠
t2.
для t1≠
t2.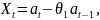 где
at
- «белый шум» μ
= 0. Тогда Xt
наз. процессом
скользящего среднего первого
порядкаМА(1).
Слагаемое at
наз. импульсом или шоком, поскольку
это единств.новая, т.е. ранее не
известная, инф-ия, кот. поступает в
процесс в каждый момент времени.
где
at
- «белый шум» μ
= 0. Тогда Xt
наз. процессом
скользящего среднего первого
порядкаМА(1).
Слагаемое at
наз. импульсом или шоком, поскольку
это единств.новая, т.е. ранее не
известная, инф-ия, кот. поступает в
процесс в каждый момент времени. ,
,
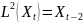 …
…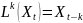 тогда
процесс МА(q)
м/б
записан короче, если заменить at-k=
Lk(at)
и
использовать фун-ию оператора
тогда
процесс МА(q)
м/б
записан короче, если заменить at-k=
Lk(at)
и
использовать фун-ию оператора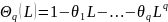
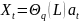
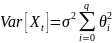
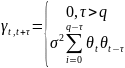
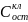 )
можно найти как сумму
и
:
=
)
можно найти как сумму
и
:
=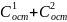
 -
- -
-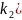 =n-
-
(1)
=n-
-
(1)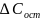 =
-
=
-

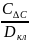 =
=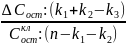 (2)
(2)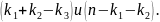
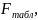 то
гип. о структурной стабильности
тенденции признают незначимой. В этом
случае мод-ние тенденции ряда следует
осуществлять с помощью кус.-лин.
модели. Если F<
то
гип. о структурной стабильности
тенденции признают незначимой. В этом
случае мод-ние тенденции ряда следует
осуществлять с помощью кус.-лин.
модели. Если F<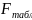 то
нет оснований отклонять нул. гип. о
структурнойстаб. тенденции. Ее
моделирование следует осуществлять
с помощью единого для всей сов-тиур-ния
тренда.
то
нет оснований отклонять нул. гип. о
структурнойстаб. тенденции. Ее
моделирование следует осуществлять
с помощью единого для всей сов-тиур-ния
тренда. 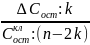
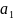 и
и
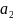 ,
а также
и
соответственно стат. незначимы. Если
же F>Fтабл,
то гипотеза о структурной стабильности
отклоняется, что означает статистическую
значимость различий в оценках пар-ров
ур-ний (1) и (2).
,
а также
и
соответственно стат. незначимы. Если
же F>Fтабл,
то гипотеза о структурной стабильности
отклоняется, что означает статистическую
значимость различий в оценках пар-ров
ур-ний (1) и (2).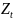 ,кот.
принимает значения 1 для всех t<t*,
принадлежащие промежутку времени до
изменения хар-ра тенденции, ее -
промежутку (1), и значения 0 для всех
t>t*
принадлежащие промежутку времени
после изменения характера тенденции,
далее промежутку (2). Гуйарати предложил
следующее уравнение регрессии:
,кот.
принимает значения 1 для всех t<t*,
принадлежащие промежутку времени до
изменения хар-ра тенденции, ее -
промежутку (1), и значения 0 для всех
t>t*
принадлежащие промежутку времени
после изменения характера тенденции,
далее промежутку (2). Гуйарати предложил
следующее уравнение регрессии: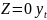 =
а + с*t+
;
(2)
=
а + с*t+
;
(2)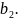

 =y_t-(T*E)
=y_t-(T*E)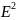
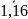 ,
найдем уровни Т для каждого момента
вр-ни (графа 5).
,
найдем уровни Т для каждого момента
вр-ни (графа 5).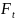 уровня временного ряда в мультипликативной
модели в соответствии с соотношением
Y=T*S*E - это произведение трендовой и
сезонной компонент. Для определения
трендовой компоненты за каждый квартал
воспользуемся уравнением тренда (1)
и получим
уровня временного ряда в мультипликативной
модели в соответствии с соотношением
Y=T*S*E - это произведение трендовой и
сезонной компонент. Для определения
трендовой компоненты за каждый квартал
воспользуемся уравнением тренда (1)
и получим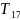 и
и
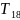 .
Значения сезонной компоненты равны:
.
Значения сезонной компоненты равны:
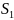 и
и
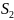 .
Таким образом,
.
Таким образом,
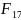 =
=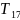 *
,
*
,
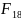 =
=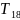 *
*

 ,
где
at
- «белый
шум» с μ0=
0. Свободный член
,
где
at
- «белый
шум» с μ0=
0. Свободный член
 часто
приравнивается к нулю.
часто
приравнивается к нулю.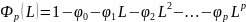 можно
коротко записать это как
можно
коротко записать это как

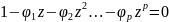 или
или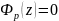 где
z—
комплексное число.
где
z—
комплексное число.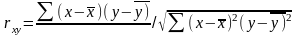
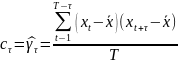 ,
,


 ,
где
yt—ВР,
являющийся реализацией процесса Yt;
,
где
yt—ВР,
являющийся реализацией процесса Yt;
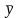 —
выборочная
средняя по данному ВР. Если временной
ряд уt
— нестационарный,
т.е. в уравнении (1) α1=1,
то в числителе получим Σ(yt-yt-1)2=Σ
ε t2.
Для нестационарного
ряда это отношение будет близко к 0.
Можно сказать, что процесс уt—
не стационарный,
если IDW≈0,
и уt
— стационарный,
если IDW≈2.
Зам:
Утверждение о стационарности процесса
не требует подтверждения рез-тами
других тестов, однако нестационарность
ставит задачу определения порядка
интегрируемости либо заключения о
том, что процесс неинтегрируем вообще.
Обычно не известно заранее, какие
компоненты содержит ВР, включает ли
он свободный член или тренд. Поэтому
использование интеграционной
статистики Д-У на этапе оценки
интегрируемости ВР без применения
дополн-ых тестов может привести к
ошибочным выводам. Для оценки
стационарности или порядка
интегрируемости данных ВР необх-мо
сопоставить расчетные значения
IDW-статистики
с критическими. Зам.
Поскольку распределение IDW-статистики
не соответствует ни одному из известных
теоретических распределений,
критические значения будут представлены
не единичными значениями, а отрезком.
Критические
значения применяются для проверки
гипотезы Н0:IDW=2
(процесс стац-ный) и альтернативной
ей гипотезы Н1:IDW≠2
(процесс не явлстац-ным). А также
гипотезы H*0
:IDW=0
(процесс нестац-ный) и альтернативной
гипотезы H*1IDW≠0
(процесс не явлнестац-ным).
—
выборочная
средняя по данному ВР. Если временной
ряд уt
— нестационарный,
т.е. в уравнении (1) α1=1,
то в числителе получим Σ(yt-yt-1)2=Σ
ε t2.
Для нестационарного
ряда это отношение будет близко к 0.
Можно сказать, что процесс уt—
не стационарный,
если IDW≈0,
и уt
— стационарный,
если IDW≈2.
Зам:
Утверждение о стационарности процесса
не требует подтверждения рез-тами
других тестов, однако нестационарность
ставит задачу определения порядка
интегрируемости либо заключения о
том, что процесс неинтегрируем вообще.
Обычно не известно заранее, какие
компоненты содержит ВР, включает ли
он свободный член или тренд. Поэтому
использование интеграционной
статистики Д-У на этапе оценки
интегрируемости ВР без применения
дополн-ых тестов может привести к
ошибочным выводам. Для оценки
стационарности или порядка
интегрируемости данных ВР необх-мо
сопоставить расчетные значения
IDW-статистики
с критическими. Зам.
Поскольку распределение IDW-статистики
не соответствует ни одному из известных
теоретических распределений,
критические значения будут представлены
не единичными значениями, а отрезком.
Критические
значения применяются для проверки
гипотезы Н0:IDW=2
(процесс стац-ный) и альтернативной
ей гипотезы Н1:IDW≠2
(процесс не явлстац-ным). А также
гипотезы H*0
:IDW=0
(процесс нестац-ный) и альтернативной
гипотезы H*1IDW≠0
(процесс не явлнестац-ным). (1). Пусть, было установлено, что в
исследуемой модели имеет место
полиномиальная структура лага, т.е.
зависимость коэффициентов регрессии
bj
от
величины лага описывается полиномом
k-й
степени.
Лаги, структуру которых
можно описать с помощью полиномов,
называют также лагами Алмон.
(1). Пусть, было установлено, что в
исследуемой модели имеет место
полиномиальная структура лага, т.е.
зависимость коэффициентов регрессии
bj
от
величины лага описывается полиномом
k-й
степени.
Лаги, структуру которых
можно описать с помощью полиномов,
называют также лагами Алмон.
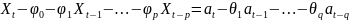

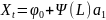 ,
где
Ψ(L)=1-ψ1L-ψ2L2-...
,
где
Ψ(L)=1-ψ1L-ψ2L2-...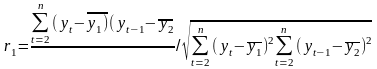 – коэффициент автокорреляции уровней
ряда первого порядка, так как он
измеряет зависимость между соседними
уровнями ряда t
и
t
-
1, т.е. при лаге 1.
– коэффициент автокорреляции уровней
ряда первого порядка, так как он
измеряет зависимость между соседними
уровнями ряда t
и
t
-
1, т.е. при лаге 1.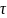 ,
ряд содержит циклические колебания
с периодичностью в
моментов времени. Если ни один из
коэффициентов автокоррел. не является
значимым,то: либо ряд не содержит
тенденции и циклических колебаний и
имеет структуру, сходную со структурой
ряда, изображенного на третьем рисунке,
либо ряд содержит
сильную нелинейную тенденцию, для
выявления кот. нужно провести дополнит.
анализ. Поэтому коэффициент автокоррел.
уровней и автокоррел. ф-ию целесообразно
использовать для выявления во ВР
наличия или отсутствия трендовой
компоненты (T)
и циклической (сезонной) компоненты
(S).
,
ряд содержит циклические колебания
с периодичностью в
моментов времени. Если ни один из
коэффициентов автокоррел. не является
значимым,то: либо ряд не содержит
тенденции и циклических колебаний и
имеет структуру, сходную со структурой
ряда, изображенного на третьем рисунке,
либо ряд содержит
сильную нелинейную тенденцию, для
выявления кот. нужно провести дополнит.
анализ. Поэтому коэффициент автокоррел.
уровней и автокоррел. ф-ию целесообразно
использовать для выявления во ВР
наличия или отсутствия трендовой
компоненты (T)
и циклической (сезонной) компоненты
(S).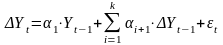 (2).
Данный
тест называется обобщенным
тестом Д-Ф
(ADF-тест).
Процедура тестирования — оценивается
значение t-критерия
Стьюдента для параметра 1.
Критические значения для ADF-теста
те же самые, что и для обычного DF-теста.
Добавим в (2) константу и линейный
тренд:
(2).
Данный
тест называется обобщенным
тестом Д-Ф
(ADF-тест).
Процедура тестирования — оценивается
значение t-критерия
Стьюдента для параметра 1.
Критические значения для ADF-теста
те же самые, что и для обычного DF-теста.
Добавим в (2) константу и линейный
тренд:
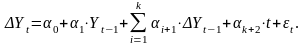 Добавленные
в уравнения лаговые компоненты никак
не изменяют верхние и нижние пороговые
значения, поэтому в качестве таблицы
критических значений для ADF-статистики
используют соответствующую таблицу
для DF-статистики. Выбор длинны лага
к
эл-тов авторегрессионной компоненты
достаточно сложная задача. Основная
цель включения дополнительных
слагаемых — обеспечение свойств
«белого шума» для случайной компоненты
t,
поэтому необходимо проверить t,
на независимость и одинаковое
распределение. Зам:
Если mах
длина лага =к, то кол-во дополнит.
слагаемых м.б. <к, т.к некот из коэф-тов
α
i+1
м.
оказаться = 0. В
качестве критериев определения
оптимальной длины лага можно
использовать информационные критерии
Акаики и Шварца. Они основаны на
принципе снижения остаточной суммы
квадратов при добавлении значимого
фактора.
Добавленные
в уравнения лаговые компоненты никак
не изменяют верхние и нижние пороговые
значения, поэтому в качестве таблицы
критических значений для ADF-статистики
используют соответствующую таблицу
для DF-статистики. Выбор длинны лага
к
эл-тов авторегрессионной компоненты
достаточно сложная задача. Основная
цель включения дополнительных
слагаемых — обеспечение свойств
«белого шума» для случайной компоненты
t,
поэтому необходимо проверить t,
на независимость и одинаковое
распределение. Зам:
Если mах
длина лага =к, то кол-во дополнит.
слагаемых м.б. <к, т.к некот из коэф-тов
α
i+1
м.
оказаться = 0. В
качестве критериев определения
оптимальной длины лага можно
использовать информационные критерии
Акаики и Шварца. Они основаны на
принципе снижения остаточной суммы
квадратов при добавлении значимого
фактора.
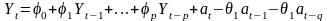 (1)
тогда
Xt
называется процессом
ARIMA(p,d,q),
т.е интегр-мым авторегрессионным
процессом скользящего среднего, где
p-порядок
авторегр-ого процесса, q-порядок
max
лага для скольз среднего, d-порядок
интегр-ти. Зам:
Свободный член φ0
приравнивается к нулю (опускается).
Большинство эмпирических ВР можно
считать реализациями процессов ARIMA.
Основная задача в анализе ВР —
специфицировать порядок модели
ARIMA(p,d,q), т.е определить пар-ры p,d,q по
св-вам ВР и оценить пар-ры ур-ния модели
и дисперсию остатков. Идентификация
модели и оценивание параметров.
Моделирование
состоит из следующих шагов. Шаг
1.
Диагностика, т.е. проверка ВР на
стац-ть, условие эргодичности: –
анализ графика ВР; – Тест на единичный
корень; – В случае нестационарности
- взятие разностей и повтор тестов; –
Оценивание автокорреляционной ф-ции
(ACF).
Шаг
2.
Выбор типов возможных процессов,
сгенерировавших этот ВР (идентификация
модели). В рез-те д.б. получены три осн
пар-ра: d — порядок интегр-ти, р и q —
порядки компонент AR и МА соотв-но.
Пар-р d легко определяется как кол-во
взятых разностей, необходимое для
получения стац-ого процесса. В случае
сомнений следует выбирать модели с
наименьшим возможным числом пар-ров.
Шаг
3.
Оценивание пар-ров для всех возможных
модели подходящими статистическими
методами: – обычный МНК; – метод
максимального правдоподобия (МПМ); –
метод минимизации квадратов ошибок
прогноза.
(1)
тогда
Xt
называется процессом
ARIMA(p,d,q),
т.е интегр-мым авторегрессионным
процессом скользящего среднего, где
p-порядок
авторегр-ого процесса, q-порядок
max
лага для скольз среднего, d-порядок
интегр-ти. Зам:
Свободный член φ0
приравнивается к нулю (опускается).
Большинство эмпирических ВР можно
считать реализациями процессов ARIMA.
Основная задача в анализе ВР —
специфицировать порядок модели
ARIMA(p,d,q), т.е определить пар-ры p,d,q по
св-вам ВР и оценить пар-ры ур-ния модели
и дисперсию остатков. Идентификация
модели и оценивание параметров.
Моделирование
состоит из следующих шагов. Шаг
1.
Диагностика, т.е. проверка ВР на
стац-ть, условие эргодичности: –
анализ графика ВР; – Тест на единичный
корень; – В случае нестационарности
- взятие разностей и повтор тестов; –
Оценивание автокорреляционной ф-ции
(ACF).
Шаг
2.
Выбор типов возможных процессов,
сгенерировавших этот ВР (идентификация
модели). В рез-те д.б. получены три осн
пар-ра: d — порядок интегр-ти, р и q —
порядки компонент AR и МА соотв-но.
Пар-р d легко определяется как кол-во
взятых разностей, необходимое для
получения стац-ого процесса. В случае
сомнений следует выбирать модели с
наименьшим возможным числом пар-ров.
Шаг
3.
Оценивание пар-ров для всех возможных
модели подходящими статистическими
методами: – обычный МНК; – метод
максимального правдоподобия (МПМ); –
метод минимизации квадратов ошибок
прогноза.
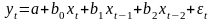 .
Наряду с лаговыми знач-ями незав-ых
переменных на вел-ну зависимой
переменной текущего периода могут
оказывать влияние ее значения в
прошлые моменты времени. Эти процессы
обычно описывают с помощью моделей
с авторегрессией:
.
Наряду с лаговыми знач-ями незав-ых
переменных на вел-ну зависимой
переменной текущего периода могут
оказывать влияние ее значения в
прошлые моменты времени. Эти процессы
обычно описывают с помощью моделей
с авторегрессией:
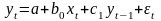 .
Интерпретация
пар-ов моделей с распределенным лагом
и моделей авторегрессии. Рассмотрим
модель с распр лагом в ее общем виде
в предположении, что максимальная
величина лага конечна и равна l:
.
Интерпретация
пар-ов моделей с распределенным лагом
и моделей авторегрессии. Рассмотрим
модель с распр лагом в ее общем виде
в предположении, что максимальная
величина лага конечна и равна l:
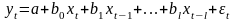
 и
представляет собой средний период,
в теч кот-ого будет происходить
изменение рез-та под воздействием
изменения фактора в момент времени
t. 2)Медианного лага — это вел-на лага
lMe,
для кот ∑ βj≈0,5.
Это период времени, в теч кот с момента
времени t будет реализована половина
общего воздействия фактора на рез-т.
и
представляет собой средний период,
в теч кот-ого будет происходить
изменение рез-та под воздействием
изменения фактора в момент времени
t. 2)Медианного лага — это вел-на лага
lMe,
для кот ∑ βj≈0,5.
Это период времени, в теч кот с момента
времени t будет реализована половина
общего воздействия фактора на рез-т.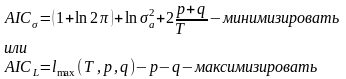
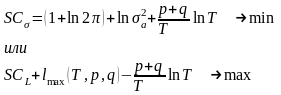
 где
lmax(T,k)
— значение логарифмической функции
правдоподобия оцениваемой модели;
где
lmax(T,k)
— значение логарифмической функции
правдоподобия оцениваемой модели;