Теорема 6.1

Для всякого потока  транспортной сети N = (G, c) справедливо равенство .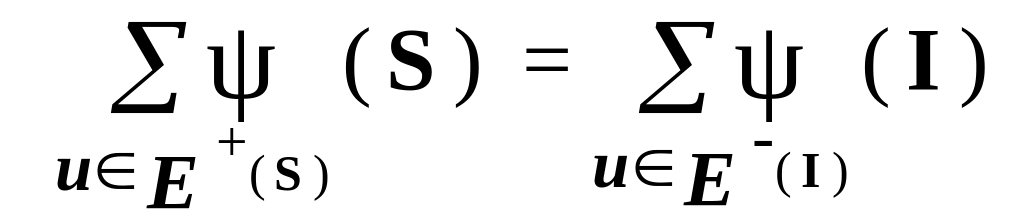

Доказательство

Возможны следующие случаи.

Случай 1. В сети N нет циклов, по всем ребрам которых проходит ненулевой поток.

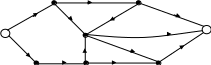
В этом случае удалим из N все такие ребра, по которым проходит нулевой поток. Тогда полученный в результате граф будет подобен графу, приведенному на рис. 6.1. В таком графе нет циклических ребер, а всякий путь может быть продолжен до пути, ведущего в S.

I S

Рис. 6.1

Построим специальное представление графа G, разместив всякую его вершину в ярусе, определяемом значением максимальной длины путей, ведущих от истока сети к этой вершине.

Для приведенного примера сети, размещение вершин по ярусам имеет вид (рис 6.2)

I S

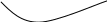
0 1 2 3 4

(номера ярусов) Рис 6.2

Если в полученном представлении некоторое ребро соединяет вершины из не соседних ярусов, то разобьем его на несколько, вводя дополнительные вершины.

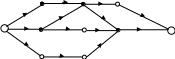
Для рассматриваемого графа G это приводит к следующему его представлению (рис. 6.3):

I S

Рис. 6.3

На этом рисунке светлыми кружками выделены добавленные вершины. Ребрами этого графа представляются только вершины соседних ярусов. При этом пропускные способности и величины потока в добавленных ребрах совпадают с этими же значениями для разбиваемых ребер.

Очевидно, что величина потока в полученной сети совпадает с величиной потока в исходной сети. Кроме того, суммарные величины входного и выходного потоков для всякого внутреннего яруса сети равны. Поэтому суммарный выходной поток истока сети, является входным потоком вершин первого, второго и последующих ярусов.

Следовательно, .

Случай 2. Пусть в G имеются элементарные циклы ненулевой длины, через каждое ребро которых проходит ненулевой поток.

Покажем, что в этом случае ресурс, циркулирующий по всякому такому циклу, не влияет на величины каждого из двух суммарных потоков: выходящего из I и входящего в S.

Преобразуем  так, чтобы, сохранив величину потока, проходящего по сети, добиться отсутствия в сети N циклов с ненулевыми потоками в ребрах.

Для этого, пока в G имеются циклические ребра, будем повторять следующие действия.

1.В графе G возьмем произвольный элементарный цикл C, по всем ребрам которого протекает ненулевой поток.

2. Найдем значение d = min((u₁), . . . , (u_r)), где u₁, . . . , u_r  ребра C.

3. Изменим функцию , уменьшив ее значения для ребер C на величину d и оставив значения  для остальных ребер без изменения.

Поскольку для каждого повторения действий 1  3 в графе появляется новое ребро, по которому течет нулевой поток, то преобразование потока  заканчивается за конечное число шагов.

Исходный поток  преобразуется в функцию *, которая также является потоком.

Кроме того, суммарные входные потоки для S (суммарные выходные потоки из I) для функций  и * являются равными, поскольку через I и S в G не проходит ни один элементарный цикл ненулевой длины.

Поскольку окончательный поток удовлетворяет условиям случая 1, то для него выполняется доказываемое равенство:

.

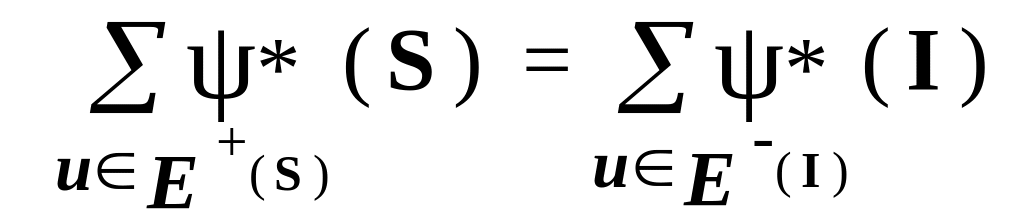Поэтому такое же равенство выполняется и для исходного потока:

.

Доказательство окончено.

Пример. Рассмотрим транспортную сеть, приведенную на рис. 6.4.

10 (5)

14(10) 17(5) 2(1) 9(4)

I 7(6) S

5(8)

11(7) 16 (7) 10(8)

9(8) 24(1)

Рис. 6.4

Здесь ребрам сети приписаны значения их пропускных способностей, в скобках указаны значения потока по ребрам сети.

Величина потока, приведенного на рис. 6.4, равна 18.

В общем случае величина потока в сети задает суммарное количество ресурса, передаваемого по сети от истока к стоку.