Вопрос №1. Математическая модель операции. Основные понятия и определения.

Операция – совокупность действий, мероприятий, объединенных единым замыслом и направленных на достижение цели.

Оперирующая сторона – совокупность лиц, устройств, автоматов, стремящихся к достижению поставленной цели и ответственных за проведение операции.

Оперирующая сторона всегда имеет в своем распоряжении некоторый запас ресурсов, и, используя и расходуя их, она добивается поставленной цели. Эти ресурсы называются активными средствами, а способы их использования, расходования – стратегиями оперирующей стороны. Оптимальными считаются стратегии, которые по некоторым соображениям явл. предпочтительнее других.

Исход операции зависит от факторов, имеющихся в распоряжении оперирующей стороны. Эти факторы назыв. контролируемыми. Неконтролируемые факторы – факторы, которые не зависят от действий оперирующей стороны и которые она изменять не вправе. Они определяют обстановку проведения операции.

Задача исследования операций заключается в выборе и количественном обосновании оптимальных стратегий с учетом обстановки проведения операции. Этими вопросами занимается исследователь операции – лицо или группа лиц, принадлежащих к оперирующей стороне.

Математическая модель – относительная истина, отражающая определенные особенности изучаемых явлений.

Виды:

1) Статистическая. Связана с ЭВМ. Позволяют наиболее полно учитывать все связи, факторы, описывающие операцию, и заменять однократное исследование сложной модели многократным исследованием простых операций.

2)Аналитические модели. С помощью алгебраических, дифференциальных, интегральных уравнений позволяют установить формульные зависимости между основными факторами операции. Используются, когда либо число параметров не слишком велико, либо зависимости между ними не очень сложные.

По сути мат. описания аналит. модели могут быть:

1) детерминированные. Все факторы, характеризующие рассматриваемую операцию, считаются известными исследователю операции.

2) стохастические содержат случайные факторы, относительно которых известны лишь законы их распределения.

По числу этапов:

1) многоэтапные используются при рассмотрении операций, развивающихся во времени, и могут быть разделены на ряд взаимосвязанных этапов.

2) одноэтапные рассматриваются в некоторый фиксированный момент времени.

№2. Оценка эффективности стратегий в условиях неопределенности.

Решение принимается в условиях неопределенности, когда невозможно оценить вероятность потенциальных результатов. Это имеет место, когда требующие учета факторы настолько новы и сложны, что невозможно получить достаточно релевантной информации, могущей помочь объективно определить вероятность, либо имеющаяся ситуация не подчиняется известным закономерностям. Поэтому вероятность определенного последствия невозможно предсказать с достаточной степенью достоверности. Неопределенность характерна для некоторых решений, принимаемых в быстро меняющихся условиях.

Сталкиваясь с неопределенностью, руководитель может использовать две основные возможности. Во-первых, попытаться получить дополнительную релевантную информацию и еще раз проанализировать проблему. Этим часто удается уменьшить новизну и сложность проблемы. При этом руководитель сочетает эту информацию с накопленным опытом, способностью к суждению или интуицией, чтобы придать ряду результатов субъективную или предполагаемую вероятность. Во-вторых, он может действовать в точном соответствии с прошлым опытом, суждениями и интуицией и сделать предположение о вероятности событий. Это необходимо, когда нет достаточно времени на сбор дополнительной информации.

{X,Y,f} f(x;y) (x;y)R

1) критерий наилучшего гарантированного результата(Вальда). Предполагает, что неконтролируемый фактор действует наихудшим для оперирующей стороны образом. Только задачи на max.

x: W1(x) = min f(x;y)

2) критерий Лапласа. Предполагается, что все неконтролируемые факторы являются случайными величинами, но т.к мы не знаем распределение вероятности, значит она плохо устанавливается статист.методом.

x: W2(x) = ∫ f(x,y) p(y) dy

Y

3)критерий Сэвиджа. Выражает соглашение о том, что для данного Y была применена стратегия X, а не лучшая стратегия. Необходимо минимизировать по X исходя из критерия наилучшего гарантированного результата.

x: W3(x) = max фи(x;y)

x в степени 0: W3(x0) = min W3(x)

Путь исходной задачи состоит в нахождении min из f(x;y).

4) критерий Гурвица: выпуклая комбинация критериев крайнего пессимизма и крайнего оптимизма. W4(x) = max f(x;y) W5(x) = альфаW4(x) + (1-альфа)W1(x)

№3. Оценка эффективности стратегий в условиях риска.

К решениям, принимаемым в условиях риска, относятся такие решения, результаты которых не являются определенными, но вероятность каждого возможного результата можно определить. Вероятность определяется в промежутке от 0 до 1 и представляет собой степень возможности совершения данного события. Сумма вероятностей всех альтернатив должна быть равна единице.

Риск при принятии решений может быть различным. В экономике различают несколько типов риска: страховой, валютный, кредитный и т.д. В зависимости от типа риска, вероятность его можно определить математическими и статистическими методами.

Наиболее желательный способ определения вероятности – объективность. Вероятность объективна, когда ее можно определить математическими методами или путем статистического анализа накопленного опыта. Вероятность может быть объективно определена, если поступит достаточно релевантной информации для того, чтобы прогноз оказался статистически достоверным.

Во многих случаях организация не располагает достаточной информацией для объективной оценки вероятности. В таком случае часто руководители используют суждения о возможности совершения альтернатив с той или иной субъективной или предполагаемой вероятностью.

1) критерий ожидаемого значения: В данном критерии мы считаем для каждой из стратегий математическое ожидание:

2) критерий мат.ожидания – дисперсии:

Пусть известен (к)- коэффициент склонности к риску, тогда при выборе наилучшей стратегии мы можем ориентироваться не только на ожидаемый доход, но и на его отклонение.

№4. Постановка задачи ЛП, основные виды задач ЛП. Геометрическая интерпретация.

Линейное программирование – это направление математического программирования, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейным критерием.

Необходимым условием постановки задачи линейного программирования являются ограничения на наличие ресурсов, величину спроса, производственную мощность предприятия и другие производственные факторы.

Сущность линейного программирования состоит в нахождении точек наибольшего или наименьшего значения некоторой функции при определенном наборе ограничений, налагаемых на аргументы и образующих систему ограничений, которая имеет, как правило, бесконечное множество решений. Каждая совокупность значений переменных (аргументов функции F), которые удовлетворяют системе ограничений, называется допустимым планом задачи линейного программирования. Функция F, максимум или минимум которой определяется, называется целевой функцией задачи. Допустимый план, на котором достигается максимум или минимум функции F, называется оптимальным планом задачи.

Система ограничений, определяющая множество планов, диктуется условиями производства. Задачей линейного программирования (ЗЛП) является выбор из множества допустимых планов наиболее выгодного (оптимального).

Виды задач:

1. Стандартная задача лп: 2. Каноническая задача лп:

Стандартная задача важна ввиду наличия большого числа прикладных моделей, сводящихся наиболее естественным образом к этому классу задач ЛП. Основные вычислительные схемы решения задач ЛП разработаны именно для канонической задачи.

3. Общая задача ЛП:

В этой задаче часть ограничений носит характер неравенств, а часть является уравнениями. Кроме того, не на все переменные наложено условие неотрицательности:

Здесь . Ясно, что стандартная задача получается как частный случай общей при ; каноническая — при .

Все три перечисленные задачи эквивалентны в том смысле, что каждую из них можно простыми преобразованиями привести к любой из двух остальных.

Линейная форма , подлежащая максимизации (или минимизации), называется целевой функцией.

Геометрическая задача ЛП представляет собой отыскание такой точки многогранника решений, координаты которой доставляют линейной функции линейное значение, причем допустимыми решениями служат все точки многогранника решений:

1)Построить множество допустимых пар(планов)

2) Нарм. … уровня целевой функции для нахождения максимума.

№5. Понятия крайней точки и опорного плана. Теорема об оптимальности крайней точки.

Точка называется крайней (угловой) точкой выпуклого множества Х, если не существует точек , и числа таких, что .

Векторы x, y, z из называются линейно независимыми, если равенство . Возможно только в случае, когда все числа .

План называется опорным планом задачи

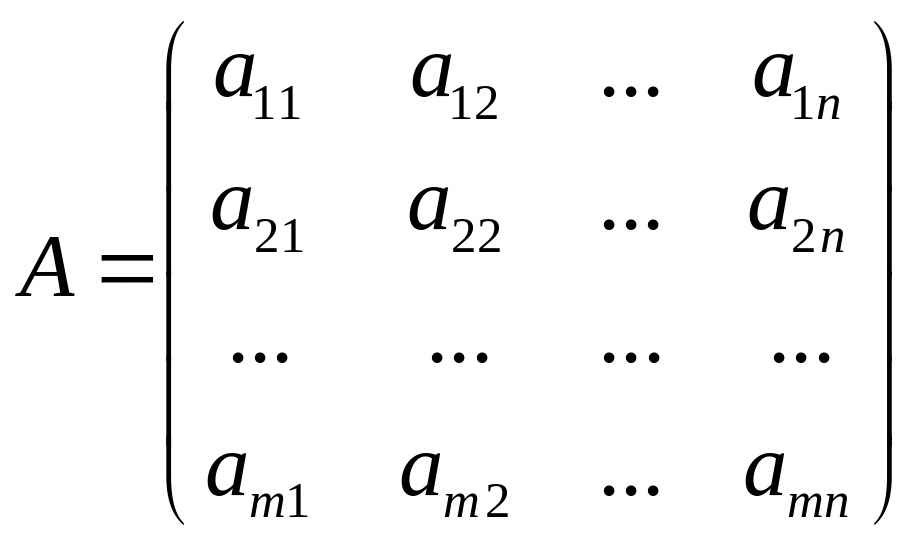, если векторы входящие в разложение с положительными коэффициентами ( >0), линейно независимы.

Опорный план называется невырожденным, если он содержит ровно m положительных компонентов, в противном случае он назыв. вырожденным.

Теорема 2:

Если задача имеет решение, то максимальное значение линейной функции <c,x>= на выпуклом множестве допустимых планов X достигается хотя бы в одной из крайних точек множества X. Если максимальное значение целевая функция принимает в нескольких крайних точках, то она принимает его в любой точке, являющейся выпуклой комбинацией этих крайних точек.

№6. Идея симплекс-метода. Признак оптимальности опорного плана, признак неограниченности целевой функции на множестве допустимых планов.

Идея с-м состоит в том, чтобы сначала попасть в крайнюю точку, затем проверить план на оптимальность. Если план оптимальный, то алгоритм работу закончил. Если план неоптимальный, то следует по ребру перейти в смежную крайнюю точку, в которой значение целевой функции будет лучше, чем в предыдущей. Затем нужно снова проверить полученный план на оптимальность. Таким образом, с-м будет двигаться от одной крайней точки к другой, последовательно улучшая значение целевой функции. Переходы будут закончены при достижении целевой функции оптимального значения.

Признак оптимальности:

Невырожденный опорный план задачи (4.3) и 4.4 оптимален тогда и только тогда, когда все оценки свободных переменных неотрицательны

Признак неограниченности:

Если в индексной строке с-таблицы задачи 4.3 и 4.4 содержится отрицательная оценка , а в соответствующем столбце переменной нет ни одного положительного элемента, то целевая функция не ограничена сверху на множестве допустимых планов.