
- •1.Классификация уравнений в частных производных в точке (в области).
- •2.Приведение к каноническому виду уравнения 2 – го порядка в случае
- •3.Приведение к каноническому виду уравнений второго порядка с постоянными коэффициентами в случае независимых переменных.
- •4.Постановка задачи Коши. Теорема Ковалевской
- •5.Корректность постановки задачи. Пример Адамара.
- •6. Уравнения колебания струны
- •7.Малые продольные колебания упругого стержня
- •8.Малые крутильные колебания вала.
- •9. Телеграфное уравнение. Частные случаи.
- •10. Уравнение колебания мембраны
- •11. Уравнение теплопроводности
- •12.Задача Коши для одномерного волнового уравнения.
- •13.Осреднение функции на сфере и трехмерное волновое уравнение.
- •14.Задача Коши для трехмерного волнового уравнения. Формула Кирхгофа
- •15.Задача Коши для волнового уравнения. Метод спуска. Формула Пуассона.
- •16.Единственность и устойчивость решения задачи Коши для волнового уравнения.
- •17.Элементарное (фундаментальное) решение уравнения теплопроводности.
- •18.Задача Коши для уравнения теплопроводности.
- •19.Принцип экстремума для уравнений теплопроводности.
- •20.Единственность и устойчивость решения задачи Коши для уравнения теплопроводности.
- •21.Задача Штурма-Лиувилля. Свойства собственных значений и собственных функций.
- •22.Метод Фурье решения смешанных задач для однородных уравнений гиперболического и параболического типа.
- •23.Самосопряженность дифференциального оператора. Формулы Грина.
- •24.Смешанные задачи для неоднородных уравнений. Задачи с неоднородными граничными условиями.
- •25.Единственность решений смешанных задач для волнового уравнения и уравнения теплопроводности.
- •26.Свободные колебания прямоугольной мембраны.
- •27.Уравнение Бесселя. Функции Бесселя.
- •28.Радиальные колебания круглой мембраны.
- •29.Крутильные колебания вала с диском на конце.
- •30.Уравнение эллиптического типа.
- •31. Определение гармонической функции. Фундаментальное решение уравнения Лапласа
- •32. Решение задачи Дирихле для ур-я Лапласа внутри и вне круга.
- •33.Внутренняя и внешняя задача Неймана для круга. Необходимое условие существования. Теорема Гаусса
- •34. Метод Фурье решения задач Дирихле и Неймана для круговых областей.
- •35. Интегральное представление произвольной функции
- •36. Свойства гармонических функций: аналитичность и теорема о среднем на сфере
- •37.Свойства гармонических функций: принцип максимума/минимума.
- •38 Единственность и устойчивость решения задачи Дирихле.
- •39. Функция Грина в задаче Дирихле.
- •40.Функция Грина в задаче Неймана.
- •41.Формула Пуассона решения внутр. Задачи Дирихле для шара
- •42.Формула Пуассона решения задачи Дирихле для круга
- •43.Неравенство Харнака. Теорема Лиувилля
- •44. Поведение производных гармонической функции на бесконечности.
- •45. Единственность решения задачи Неймана.
- •46.Потенциалы:объемный, простого слоя, двойного слоя.
- •47. Свойства объемного потенциала
- •48. Свойства потенциала простого слоя
- •49.Свойства потенциалов двойного слоя.
- •50.Сведение краевых задач к интегральным уравнениям
4.Постановка задачи Коши. Теорема Ковалевской
Б удем
рассматривать линейное ур-ние 2-го
порядка. Любое линейное ур-ние можно
записать в виде:L[n]=
удем
рассматривать линейное ур-ние 2-го
порядка. Любое линейное ур-ние можно
записать в виде:L[n]=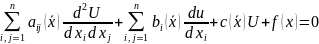 (1)
(1)
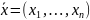
В
пространстве
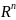 зададим незамкнутую без самопересечений
поверхность Γ ур-нием g(
зададим незамкнутую без самопересечений
поверхность Γ ур-нием g( )=0
)=0
Причем
будем считать что ф-ция g
является дважды непрерывно дифференцируемой:
g( и считаем такие, что grad
и считаем такие, что grad
 :
:
grad
g(
)=(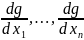 ).Обозначим
через
).Обозначим
через
 часть поверхности Γ, лежащей в области
D,т.е.
часть поверхности Γ, лежащей в области
D,т.е. .
.
Будем
предполагать, что область D
с поверхностью Γ разбиваеться на две
подобласти D(1)
и D(2).На
поверхности
зададим два условия на неизвестную
функцию U(x)
удовлетворяющую уравнению 1: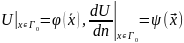 (2)
(2)
Функции 𝞿 и 𝟁 считаються замкнутыми ,n-единичная длина поверхности.
Условие
2 наз.начальными условиями. Таким образом
требуется найти функцию U∊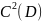 ,которая удовлетворяет ур-нию 1 в области
D
и начальным условиям 1 на поверхности
.В частности, если поверхность Γ являеться
плоскость
,которая удовлетворяет ур-нию 1 в области
D
и начальным условиям 1 на поверхности
.В частности, если поверхность Γ являеться
плоскость
 ,то начальное условие принимает вид:
,то начальное условие принимает вид:


Функция
удовлетворяющая уравнению 1 и начальным
условиям 2 наз.классическим решением
задачи Коши. Отметим что не для всех
функций 𝞿
и 𝟁
такое решение существует: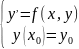 ,f(x,y)=
,f(x,y)= то существует решение y=
то существует решение y=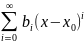 если f(x,y)
аналитическая.
если f(x,y)
аналитическая.
Если
коэффициенты
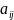 ,
, ,с
и функция f(x,y)
являються формулами аналитическими в
окружности точки
,с
и функция f(x,y)
являються формулами аналитическими в
окружности точки
 , а начальные функции 𝞿
и 𝟁
также аналитические то существеут
некоторая окрестность точки
,в которой решение задачи 1 и 2 существует,
при этом оно единственно в классе
аналитических функций.
, а начальные функции 𝞿
и 𝟁
также аналитические то существеут
некоторая окрестность точки
,в которой решение задачи 1 и 2 существует,
при этом оно единственно в классе
аналитических функций.
5.Корректность постановки задачи. Пример Адамара.
Задача считается корректно поставленной, если:
решение этой задачи существует;
решение должно быть единственным;
решение должно быть устойчиво
Приведем пример задачи, не корректно поставленной.

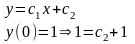
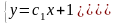 -
не корректно поставленная задача.
-
не корректно поставленная задача.
Приведем пример задачи, в которой нарушается устойчивость решений (пример Адамара).
Рассмотрим задачу :

 и
и
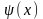 -
некоторые известные функции.
-
некоторые известные функции.
Пусть
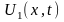 - решение задачи. Рассмотрим еще одну
задачу:
- решение задачи. Рассмотрим еще одну
задачу:
Пусть
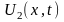 -
решение этого уравнения. Составим
разность
-
решение этого уравнения. Составим
разность
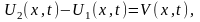 тогда
тогда
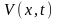 - решение задачи
- решение задачи
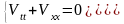
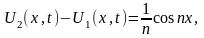 при
при


Найдем
решение задачи для функции
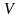 в виде
в виде

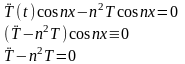
 ,
,

 - задача Коши для лин. уравнения с
пост.коэф.2 – го пор.
- задача Коши для лин. уравнения с
пост.коэф.2 – го пор.
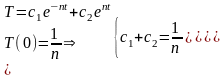
 .
.
Таким
образом,
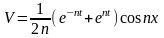
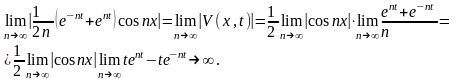
Малые изменения начальных данных привели к большой разности решений.
6. Уравнения колебания струны
П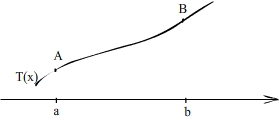 од
струной мы будем понимать упругую нить,
не сопротивляется изгибу.
од
струной мы будем понимать упругую нить,
не сопротивляется изгибу.
Будем
считать колебания струны малыми. Малость
колебаний означает, что квадратами
величин отклонения точек струны от
равновесия и квадратами производных
по
 можно пренебречь. В положении равновесия
струна совпадает с осью
можно пренебречь. В положении равновесия
струна совпадает с осью
 .
При возмущении точек струны будут
отклоняться от этой оси. Величину этого
отклонения обозначим через
.
При возмущении точек струны будут
отклоняться от этой оси. Величину этого
отклонения обозначим через
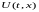 .
.
В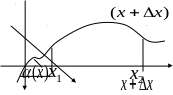 ыделим
участок струны заключенный между
ыделим
участок струны заключенный между
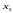 и
и
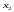 .
В положении равновесия длинна этого
участка
.
В положении равновесия длинна этого
участка
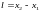 .
Выведем этот участок из положения
равновесия и посчитаем длину АВ
.
Выведем этот участок из положения
равновесия и посчитаем длину АВ
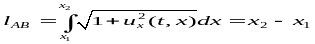
В процессе колебаний длина невозмущенного участка струны не изменяется.
В силу закона (удлинение пропорционально приложенной силе) приходим к выводу, что в процессе колебаний сила натяжения струны не меняется.
Обозначим
T(x)
сила натяжения в точке струны с координатой
 .
Выделим участок струны
.
Выделим участок струны
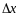 -
-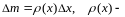 линейная
плотность струны.
линейная
плотность струны.
Если
мы зафиксируем точку х, тогда
 дает
закон движения точки х.
дает
закон движения точки х.
 -скорость
движения,
-скорость
движения,
 -ускорение,
-ускорение,
 .
.
Обозначим
через
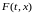 величину силы, приложенную в точки х в
момент времени t.
Считают что эти силы расположены в
плоскости XU
и параллельны оси U.
величину силы, приложенную в точки х в
момент времени t.
Считают что эти силы расположены в
плоскости XU
и параллельны оси U.
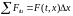 -силы
натяжения точек струны, найдем теперь
проекцию сил натяжения на ось U.
-силы
натяжения точек струны, найдем теперь
проекцию сил натяжения на ось U.
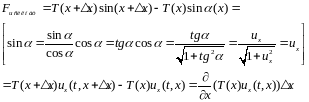
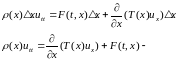 уравнения
колебаний струны.
уравнения
колебаний струны.
Если струна однородная, то
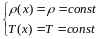 .
Тогда
.
Тогда

