2. Неперервність ф-ї багатьох змінних.

Озн: Нехай ф-я z=f(М) визначена на множині D і точка М₀D, довільний окіл М ₀ містить точку з D ≠ М₀ ця ф-я називається неперервною у точці М₀, якщо 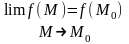_(1).

Якщо у т. М₀ рівність (1) не виконується, ф-я наз. розривною у точці М₀, а саму точку М₀ наз. точкою розриву ф-ї.

Позначимо через х=х-х₀, у=у-у₀, z=f(М)-f(М₀)=f(x,y)-f(x₀,y₀)

Величини х, у називають приростами аргументів x і y, а величина z наз. повним приростом ф-ї.

Запишемо формулу (1) у вигляді:

f(x,y) в т. М₀(х₀, у₀)з (1) сліду., що 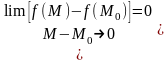↔ 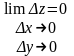(2)

Рівність (2) дає можливість сформулювати іще одне еквівалентне означення неперервності ф-ї багатьох змінних у точці.

Озн: Нехай т. М₀ відповідає переліченим вище вимогам. Ф-я z=f(М)наз. неприливною в цій т., якщо її повний приріст в т. М₀ → 0, якщо до 0 прямують приріст її аргументів.

Озн:Ф-ю z=f(М) наз. неперервною на множині D якщо вона неперервна у кожній точці D.

Озн: множина наз. звязною, якщо разом з будь-якими 2 своїми точками, вона містить непереривну криву, яка їх сполучає. Множина наз. відкритою, якщо її точка міститься у множині разом із деяким своїм околом.

Озн: Точка М множини D наз. внутрішньою, якщо вона належить множині D разом із деяким своїм околом.

Озн: Областю наз. відкриту связну множину.

Озн: Точка наз. межовою точкою для даної множини, якщо кожний її окіл містить точки, які належать даній множині, так і точки, які даній множ. не належать. Множина межових точок утв. межу даної множини.

Множина разом з її межею утв. замкнену множину

Озн: Множина наз. обмеженою, якщо існує коло скінченного радіусу, який містить у собі дану множину.

Сформулюємо без доведення основні теореми для неперервних ф-й визначених на такій множині:

Теорема 1: Якщо ф-я z=f(М), неперервна на замкненій обмеженій області D, то ця ф-я обмежена на D: C>0:M|f(M)|C.

Теорема 2: Якщо ф-я z=f(М), неперервна у замкненій обмеженій області, то вона набуває на ній свого найбільшого і найменшого значення.

Теорема 3: Якщо ф-я z=f(М), неперервна у замкненій обмеженій області D і виконується нерівність

f(М₁) f(М₂), де М₁ і М₂ D, то існує т. M₀D, така що f(М₀)=, зокрема, якщо f(М₁)0, а f(М₂)0 M₀D: f(М₀)=0.

3. Частинні похідні. Диференціал функцій багатьох змінних.

Нехай ф-я z=f(М) визначена на множині D. Точка М(x,y) належить D. Надамо змінній х приріст х, але так щоб точка М₁(х+х,у) належала D. Позначимо через _хz= f(х+х,у)-f(x,y), величину _хz наз. частинним прирістом ф-ї z=f(М) по змінній x у точці М по змінній x. Аналогічно визначається частинний приріст ф-ї по змінній у: _хz= f(х+х,у)-f(x,y).

Озн:

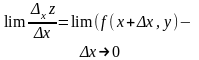
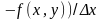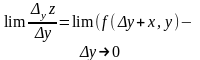
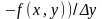Якщо існує скінчена границя , то її наз. частинною похідною ф-ї z=f(x,y) у точці М(x,y) і: f/x, z/x, f’_x,z’_x. Аналогічно визначається частинна похідну ф-ї z=f(x,y) по змінній у: . Яка позначається: f/у, z/у, f’_у,z’_у .

Якщо ідеться про значення частинної похідної у конкретній т. М₀(х₀, у₀) це позначають f(х₀,у₀)/x, z’_x_М0.

Як випливае з озн. част. похідної для її знах. застосовують ті самі формули і правила, які використовуються для функції 1-ї змінної. Наприклад для знах. f/x у функції z=f(x,y) змінну x вважають змінною, а y-сталою.

Якщо на множині D похідну f/x розглядають як функцію, то від неї можна в свою чергу також знах. частинні похідні. Якщо цю функцію про диференціювати по X, одержимо част. похідну

2-го порядку f”_xx=(f’_x)’_x або  ²f /x²= /x( f /x)

Таким чином для ф-ї двох змінних z=f(x,y) можна говорити про чотири частинних похідних другого порядку: f”_xx, f”_уу ,f”_xу ,f”_уx .

Виявляється, що для мішаних похідних у загальному випадку порядок диф. є суттєвим.

Теорема Шварца:

Якщо ф-я z=f(x,y) разом з своїмі част. похідними f’_x, f’_у, f’_xу, f’_ух визначені у деякому околі точки М₀ і в цій точці мішані похідні f”_xу; f”_yx неперервні в т. М₀ , то f”_xу|_M0=f”_yx|_M0

Наведена теорема справедлива для будь-яких мішаних похідних, які відрізняються лише порядком.

Нехай ф-я z=f(x,y) належить D,т. М(x,y) належить D. Надамо змінним х та у прирісту відповідно х,у, але так щоб М₂(х+х,у+у) належала D . Величину z= f(х+х,у+у)- f(x,y) (1) наз. повним приростом ф-ї z=f(x,y) у точці М.

Озн. Ф-я z=f(x,y) наз. диференційною у точці М, якщо її повний приріст (1) в цій точці можна у вигляді z=Ах+Ву+x+y (2), де А,В –дійсні числа, які не залежать від х,у;х,у), х,у) – нескінченно малі ф-ї, якщо х, у0.

Теорема 1(неперервність диференцируємої ф-ї): Якщо ф-я z=f(x,y) диференційна у точці М, то вона неперервна в цій точці.

Доведення:

Перейдимо у рівності (2) до границі при х→0; у→0 одержимо що z →0 Тобто ф-я z=f(x,y) неперервна у точці М.

Теорема 2(існування частинних похідних диференцируємої ф-ї): Якщо ф-я z=f(x,y) диференційна в точці М, то в цій точці вона має частинні похідні 1-го порядку по змінним x і у причому урівності (2) А=f /x, B=f /y

Теорема 3(достатні умови диференцируємості): Якщо ф-я z=f(x,y) визначена у деякому околі т. М і має частинні похідні f /x, f /y які є неперервними в т. М, то ф-я z=f(x,y) диференційна в точці М.