
- •Функція багатьох змінних. Границя функції багатьох змінних.
- •2. Неперервність ф-ї багатьох змінних.
- •3. Частинні похідні. Диференціал функцій багатьох змінних.
- •4. Повний диференціал функції багатьох змінних. Диференціали вищих порядків.
- •5. Похідні складної ф-ї багатьох змінних. Диференціал складної ф-ї багатьох змінних.
- •6. Екстремум ф-ї 2 змінних. Необхідні і достатні умови.
- •7. Невласні інтеграли 1 роду.
- •8. Невласні інтеграли 2-го роду.
- •Аналогічно визнач. Невласний інтеграл 2-го роду, якщо особливою є точка а.
- •У випадку якщо особливими є точки а і в, невласний інтеграл визнач. Так
- •9.Числові ряди. Найпростіші властивості.
- •10.Достатні ознаки збіжності додатних числових рядів. Приклади. А).Ознаки порівняння додатніх числових рядів.Приклади.
- •11. Знакопочередні ряди. Ознака Лейбніца. Знакозмінні ряди. Абсолютна і умовна збіжності.
- •12.Функціональні ряди. Поняття рівномірної збіжності. Ознака Вейєрштраса
- •13. Степеневі ряди
- •14. Ряд Тейлора
- •15. Тригонометрический ряд Фур’є
- •16. Подвійний інтеграл умови його існування і властивості.
- •1.Функція багатьох змінних. Границя функції багатьох змінних.
8. Невласні інтеграли 2-го роду.
Нехай
ф-я f(x)
визначена на проміжку [a,b)
точку х=b
назвемо особливою точкою ф-ції f(x)
якщо lim
f(x)=
коли х
b->0.
Озн. Нехай f(x)
визначена на проміжку [a,b)
де точка b
- особлива і інтегровна на будь-якому
відрізку [a,b-
ε). Якщо існує границя

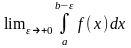 то її наз. невласним інтегралом 2-го
роду і позначають
то її наз. невласним інтегралом 2-го
роду і позначають
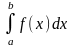 .
.
Тобто за озн. = (1)
Якщо границя в (1)існує і скінченна, ф-цію f(x) наз. інтегровною на проміжку[a;b], а сам невласний інтеграл наз. збіжним. У випадку, якщо границя в (1) не існує або нескінченна,то ф-цію f(x) наз. неінтегровною на [a;b] а сам невласний інт-л наз-ся розбіжним.
:
Аналогічно визнач. Невласний інтеграл 2-го роду, якщо особливою є точка а.
=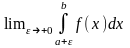 (2)
(2)
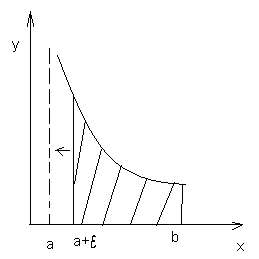
У випадку якщо особливими є точки а і в, невласний інтеграл визнач. Так
=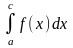 +
+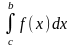
(3)
де с – довільна точка із інтервала [a;b]
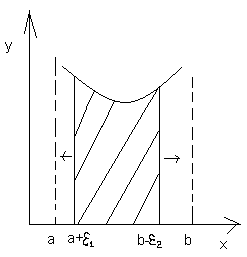
Інтеграл (3) вважаєм збіжним якщо збігаються обидва інтеграла у правій частині (3) Можна довести, що інтаграл (3) не залежить від вибору внутрішньої точки с. У випадку якщо особливою точкою є внутрішня точка відрізка [a;b] невласний інтеграл 2-го роду визнач так
=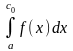 +
+

(4)
де т. с0 – особлива точка ф-ції f(x). Інтеграл (4) вважають збіжним, якщо збігаються обидва інтеграли у правій частині (4)
 Як
і невласні інтеграли 1-го роду не є
границями інтегральних сум, а визнач.
як інтеграли із змінними межами
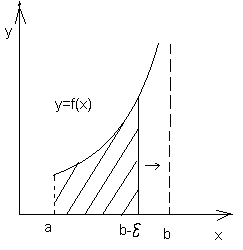
інтегрування. Геом. зміст інтегралів
(1) – (4) полягає в тому, щоб вони визначали
площу необмеженої поверхні
Як
і невласні інтеграли 1-го роду не є
границями інтегральних сум, а визнач.
як інтеграли із змінними межами
інтегрування. Геом. зміст інтегралів
(1) – (4) полягає в тому, щоб вони визначали
площу необмеженої поверхні
Наведемо далі деякі достатні ознаки збіжності невласних інтегралів 2-го роду. Сформулюємо для інтегралів виду (1). Для виду (2) –(4) формулюються аналогічно.
Теорема 1( ознака порівняння)
Нехай
ф-ції f(x)
і g(x)
додатні і неперервні на проміжку [a;b)
і b
– особлива точка 2-х ф-цій. Якщо для всіх
х що належать [a;b)
існує нерівність 0f(x)g(x)
від збіжності інтегралу
 випливає збіжність
.
А із розбіжності
випливає розбіжність
.
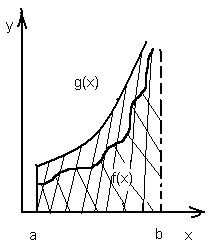
Наведена теорема має такий геом. зміст:
випливає збіжність
.
А із розбіжності
випливає розбіжність
.
Наведена теорема має такий геом. зміст:
Якщо площа більшої за розміром обл. є скінченне число, то площа меншої обл. також скінченна. У випадку, якщо площа меншої обл. нескінченна величина, то площа більшої обл. також нескінченна.
 .
.
Теорема 2 (гранична ознака порівняння)
Нехай
ф-ції f(x)
і g(x)
неперервні додатні на проміжку [a;b)
і т. в- особлива точка обох ф-цій. Якщо
 ,
то інтеграли
і
або одночасно збігаються, або одночасно
розбігаються.
,
то інтеграли
і
або одночасно збігаються, або одночасно
розбігаються.
Наведені теореми 1 і 2 справедливі лише для додатніх ф-цій. Для знакозмінних ф-цій справедлива
Теорема
3:
Нехай f(x)
неперервна на проміжку [a;b),
т. в – особлива. Якщо збігаеться
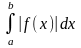 то збігається і інтеграл
.
Твердження обернене до твердження
данної теореми неправильне. Із збіжності
не випливає збіжність
то збігається і інтеграл
.
Твердження обернене до твердження
данної теореми неправильне. Із збіжності
не випливає збіжність
Відрізняють наступні випадки:
якщо разом з інтегралом збігається інтеграл наз. абсолютно збіжним
У випадку якщо збіг. а розбіжний, інтеграл наз. збіжним умовно.
