2. Формула Эйлера для определения критической силы при расчете на устойчивость.

   Для шарнирно закрепленного, центрально-сжатого стержня постоянного сечения (рис.8.2). I Формула Эйлера имеет вид:

   

   где Е - модуль продольной упругости материала стержня;

   J_min - минимальный момент инерции поперечного сечения стержня.

   Для стержней с другими видами закрепления формулу Эйлера записывают в виде:

   

   где 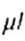- приведенная длина стержня;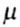

   - коэффициент приведения длины.

   Выражение "приведенная длина" означает, что в формуле Эйлера с помощью коэффициента все случаи закрепления концов стержня можно привести к основному, шарнирному закреплению.

   Коэффициент приведения длины иногда можно оценить по числу полуволн n, по которым выпучится стержень, теряя устойчивость, а именно, можно принять

   

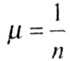
   На рис. 8.2 показаны наиболее часто встречающиеся на практике случаи закрепления концов стержня и соответствующие им значения коэффициента

   

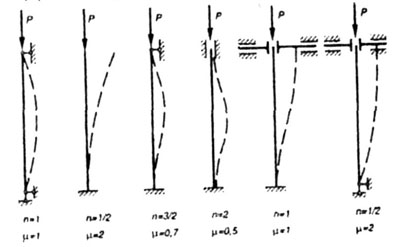
   Рис. 8.2

   Формула Эйлера применима только о пределах выполнения закона Гука, когда критическое напряжение 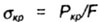не превышает предел пропорциональности материала стержня, так как эта формула была введена с помощью зависимости

   

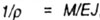
   в свое время полученной на основании закона Гука.

   Применимость формулы Эйлера можно определить, оценив гибкость стержня и сравнив эту гибкость с ее предельным значением. Гибкость стержня равна

   

   где

   - минимальный радиус инерции (геометрическая характеристика сечения);

   - минимальный момент инерции площади сечения стержня.

   Значение предельной гибкости получается из условия

   

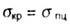
   Предельная гибкость равна

   

3. Условие устойчивости и решение 3-х задач на его основе.

В основном рассматриваются два вида расчетов:

1) проверочный, 2) проектировочный.

При проверочном расчете определяются критические напряжения и уточняется Коэффициент запаса устойчивости .

При проектировочном расчете осуществляется подбор рационального сечения, используя геометрические характеристики сечений, а именно площадь поперечного сечения , осевые моменты инерции , радиусы инерции .

4. Его не будет.

5. Формула для определения результирующих нормальных напряжений при косом изгибе.

Косым изгибом называется вид нагружения, при котором плоскость действия изгибающего момента не проходит ни через одну из главных осей сечения.

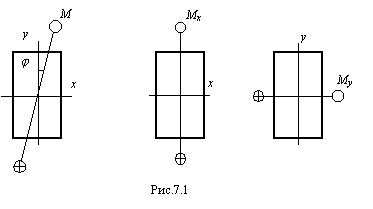Напряжения и перемещения при косом изгибе найдем, используя принцип независимости действия сил. Косой изгиб рассматривается при этом как сочетание двух плоских изгибов во взаимно перпендикулярных плоскостях (рис.7.1).

Нормальные напряжения в любой точке поперечного сечения могут быть вычислены как алгебраическая сумма напряжений, возникающих от моментов M_x и M_y:

,

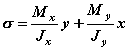где , ,

 - угол отклонения плоскости действия M от вертикали.

Для определения положения опасной точки сечения и записи условия прочности необходимо записать уравнение нейтральной линии (н.л.) как геометрического места точек сечения, в которых напряжения равны нулю.

У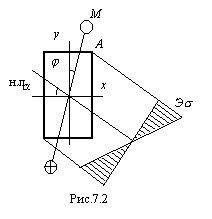 равнение нейтральной линии имеет вид:

, или .

Отсюда следует, что если , то плоскость действия момента М и нейтральная линия не перпендикулярны друг другу (в отличие от плоского изгиба).

Максимального значения в сечении нормальные напряжения достигают в наиболее удаленных от нейтральной линии точках А и В (рис.7.2). Эти точки являются опасными в данном сечении.

Условие прочности в т.А имеет вид:

,

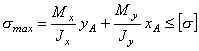где x_A, y_A - координаты точки A.

Для сечений, вписывающихся в прямоугольник (швеллер, двутавр и др.), в точках с координатами x_max и y_max, условие прочности может быть записано в виде

.

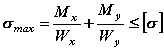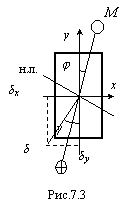
Прогиб при косом изгибе определяется как геометрическая сумма прогибов вдоль осей и (рис.7.3) по формуле .

Направление прогиба определяется углом

.

Из формулы видно, что направления прогиба балки будет совпадать с плоскостью действия момента при J_x = J_y . Если моменты инерции сечения не равны между собой , то направление прогиба и положение плоскости действия момента не совпадают (рис.7.3).