
- •16.1. Двойной интеграл.
- •16.1.3. Свойства двойного интеграла.
- •16.1.3.3.Интеграл от единичной функции по области равен площади этой области: .
- •16.1.3.5. Теоремы об оценке интеграла.
- •16.1.4. Вычисление двойного интеграла. Двукратный (повторный) интеграл.
- •16.1.5. Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах.
- •16.1.6. Задачи на двойной интеграл.
- •16.1.7. Приложения двойного интеграла.
- •10. §3 Вычисление двойного интеграла в полярных координатах; обобщенные полярные координаты.
- •Тройной интеграл. Его основные свойства и приложения. Вычисление тройного интеграла
- •Поверхностный интеграл первого рода [править]Определение
- •[Править]Параметрическая форма
- •[Править]Свойства
- •[Править]Поверхностный интеграл второго рода [править]Определение
- •[Править]Связь между поверхностными интегралами второго и первого рода
- •[Править]Свойства
- •Уравнения, допускающие понижение порядка
- •1. Уравнения, не содержащие искомой функции и нескольких последовательных производных.
- •2. Уравнения, не содержащие явно независимой переменной.
- •3. Уравнения, однородные относительно .
- •4. Обобщенно - однородные уравнения.
- •5. Уравнение в точных производных.
- •Определение 3
- •Примеры решения задач
- •Решение.
Примеры решения задач
Пример
1. Исследовать
сходимость ряда  .
.
Решение.
Применим
признак сходимости Даламбера. Сначала
запишем формулы для
-го
и
-го
членов ряда:

Затем найдем предел отношения -го члена ряда к -му при :

И
последнее, сделаем вывод о сходимости
ряда, сравнив полученное значение
предела с 1. Поскольку ![]() ,
то данный ряд расходится.
,
то данный ряд расходится.
Ответ: ряд расходится.
41 Интегральный признак сходимости числового ряда
Основные определения и понятия.
Пусть
мы имеем числовую последовательность ![]() ,
где
,
где ![]() .
Приведем
пример числовой последовательности:
.
Приведем
пример числовой последовательности: ![]() .
Числовой
ряд –
это сумма членов числовой последовательности
вида
.
Числовой
ряд –
это сумма членов числовой последовательности
вида ![]() .
В
качестве примера числового ряда можно
привести сумму бесконечно убывающей
геометрической прогрессии со знаменателем q
= -0.5:
.
В
качестве примера числового ряда можно
привести сумму бесконечно убывающей
геометрической прогрессии со знаменателем q
= -0.5: 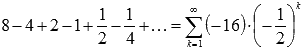 .
.
![]() называют общим
членом числового ряда или k–ым членом
ряда.
Для предыдущего примера
общий член числового ряда имеет
вид
называют общим
членом числового ряда или k–ым членом
ряда.
Для предыдущего примера
общий член числового ряда имеет
вид  .
Частичная
сумма числового ряда –
это сумма вида
.
Частичная
сумма числового ряда –
это сумма вида ![]() ,
где n –
некоторое натуральное число.
,
где n –
некоторое натуральное число. ![]() называют
также n-ой частичной
суммой числового ряда.
К примеру,
четвертая частичная сумма
ряда
называют
также n-ой частичной
суммой числового ряда.
К примеру,
четвертая частичная сумма
ряда 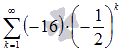 есть
есть ![]() .
Частичные
суммы
.
Частичные
суммы ![]() образуют
бесконечную последовательность частичных
сумм числового ряда.
Для нашего
ряда n
–ая частичная
сумма находится по формуле суммы
первых n членов
геометрической прогрессии
образуют
бесконечную последовательность частичных
сумм числового ряда.
Для нашего
ряда n
–ая частичная
сумма находится по формуле суммы
первых n членов
геометрической прогрессии  ,
то есть, будем иметь следующую
последовательность частичных
сумм:
,
то есть, будем иметь следующую
последовательность частичных
сумм: 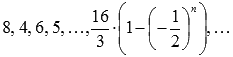 .
Числовой
ряд
.
Числовой
ряд ![]() называется сходящимся,
если существует конечный предел
последовательности частичных сумм
называется сходящимся,
если существует конечный предел
последовательности частичных сумм ![]() .
Если предел последовательности частичных
сумм числового ряда не существует или
бесконечен, то ряд
называется расходящимся.
Суммой
сходящегося числового ряда
называется
предел последовательности его частичных
сумм, то есть,
.
Если предел последовательности частичных
сумм числового ряда не существует или
бесконечен, то ряд
называется расходящимся.
Суммой
сходящегося числового ряда
называется
предел последовательности его частичных
сумм, то есть, ![]() .
В
нашем примере
.
В
нашем примере  ,
следовательно, ряд
сходится,
причем его сумма равна шестнадцати
третьим:
,
следовательно, ряд
сходится,
причем его сумма равна шестнадцати
третьим: 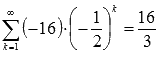 .
В
качестве примера расходящегося ряда
можно привести сумму геометрической
прогрессии со знаменателем большем,
чем единица:
.
В
качестве примера расходящегося ряда
можно привести сумму геометрической
прогрессии со знаменателем большем,
чем единица: 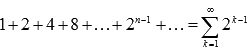 . n–ая частичная
сумма определяется выражением
. n–ая частичная
сумма определяется выражением 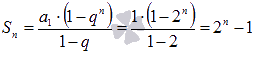 ,
а предел частичных сумм бесконечен:
,
а предел частичных сумм бесконечен: ![]() .
Еще
одним примером расходящегося числового
ряда является сумма вида
.
Еще
одним примером расходящегося числового
ряда является сумма вида ![]() .
В этом случае n–аячастичная
сумма может быть вычислена как
.
В этом случае n–аячастичная
сумма может быть вычислена как ![]() .
Предел частичных сумм бесконечен
.
Предел частичных сумм бесконечен ![]() .
Сумма
вида
.
Сумма
вида ![]() называется гармоническим
числовым рядом.
Сумма
вида
называется гармоническим
числовым рядом.
Сумма
вида 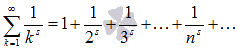 ,
где s –
некоторое действительное число,
называетсяобобщенно
гармоническим числовым рядом.
Приведенных
определений достаточно для обоснования
следующих очень часто используемых
утверждений, рекомендуем их запомнить.
,
где s –
некоторое действительное число,
называетсяобобщенно
гармоническим числовым рядом.
Приведенных
определений достаточно для обоснования
следующих очень часто используемых
утверждений, рекомендуем их запомнить.
ГАРМОНИЧЕСКИЙ РЯД
 ЯВЛЯЕТСЯ
РАСХОДЯЩИМСЯ.
Докажем расходимость
гармонического ряда.
Предположим,
что ряд сходится. Тогда существует
конечный предел его частичных сумм. В
этом случае можно записать
ЯВЛЯЕТСЯ
РАСХОДЯЩИМСЯ.
Докажем расходимость
гармонического ряда.
Предположим,
что ряд сходится. Тогда существует
конечный предел его частичных сумм. В
этом случае можно записать  и
и 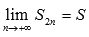 ,
что приводит нас к равенству
,
что приводит нас к равенству 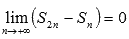 .
С
другой стороны,
.
С
другой стороны,
 Не
вызывают сомнения следующие неравенства
Не
вызывают сомнения следующие неравенства  .
Таким образом,
.
Таким образом, 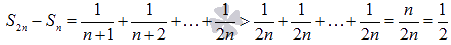 .
Полученное неравенство
.
Полученное неравенство 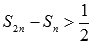 указывает
нам на то, что равенство
не
может быть достигнуто, что противоречит
нашему предположению о сходимости
гармонического ряда.
Вывод:
гармонический ряд расходится.
указывает
нам на то, что равенство
не
может быть достигнуто, что противоречит
нашему предположению о сходимости
гармонического ряда.
Вывод:
гармонический ряд расходится.
СУММА ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ ВИДА
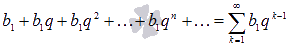 СО
ЗНАМЕНАТЕЛЕМq ЯВЛЯЕТСЯ
СХОДЯЩИМСЯ ЧИСЛОВЫМ РЯДОМ, ЕСЛИ
СО
ЗНАМЕНАТЕЛЕМq ЯВЛЯЕТСЯ
СХОДЯЩИМСЯ ЧИСЛОВЫМ РЯДОМ, ЕСЛИ 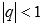 ,
И РАСХОДЯЩИМСЯ РЯДОМ ПРИ
,
И РАСХОДЯЩИМСЯ РЯДОМ ПРИ 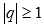 .
Докажем
это.
Мы знаем, что сумма
первых n членов
геометрической прогрессии находится
по формуле
.
Докажем
это.
Мы знаем, что сумма
первых n членов
геометрической прогрессии находится
по формуле 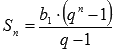 .
При
справедливо
.
При
справедливо
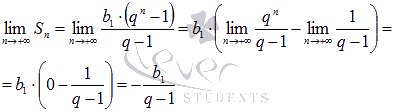 что
указывает на сходимость числового
ряда.
При q
= 1 имеем
числовой ряд
что
указывает на сходимость числового
ряда.
При q
= 1 имеем
числовой ряд 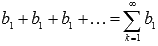 .
Его частичные суммы находятся как
.
Его частичные суммы находятся как  ,
а предел частичных сумм бесконечен
,
а предел частичных сумм бесконечен  ,
что указывает на расходимость ряда в
этом случае.
Если q
= -1,
то числовой ряд примет вид
,
что указывает на расходимость ряда в
этом случае.
Если q
= -1,
то числовой ряд примет вид 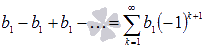 .
Частичные суммы принимают значение
.
Частичные суммы принимают значение 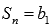 для
нечетных n,
и
для
нечетных n,
и  для
четных n.
Из этого можно сделать вывод, что предел
частичных сумм не существует и ряд
расходится.
При
для
четных n.
Из этого можно сделать вывод, что предел
частичных сумм не существует и ряд
расходится.
При  справедливо
справедливо
 что
указывает на расходимость числового
ряда.
что
указывает на расходимость числового
ряда.
ОБОБЩЕННО ГАРМОНИЧЕСКИЙ РЯД
 СХОДИТСЯ
ПРИ s
> 1 И
РАСХОДИТСЯ ПРИ
СХОДИТСЯ
ПРИ s
> 1 И
РАСХОДИТСЯ ПРИ  .
Доказательство.
Для s
= 1 получим
гармонический ряд
,
а выше мы установили его расходимость.
При s
< 1 справедливо
неравенство
.
Доказательство.
Для s
= 1 получим
гармонический ряд
,
а выше мы установили его расходимость.
При s
< 1 справедливо
неравенство  для
всех натуральных k.
В силу расходимости гармонического
ряда
можно
утверждать, что последовательность
его частичных сумм неограниченна (так
как не существует конечного предела).
Тогда последовательность частичных
сумм числового ряда
тем
более неограниченна (каждый член этого
ряда больше соответствующего члена
гармонического ряда), следовательно,
обобщенно гармонический ряд расходится
при s
< 1.
Осталось
доказать сходимость ряда
при s
> 1.
Запишем
разность
для
всех натуральных k.
В силу расходимости гармонического
ряда
можно
утверждать, что последовательность
его частичных сумм неограниченна (так
как не существует конечного предела).
Тогда последовательность частичных
сумм числового ряда
тем
более неограниченна (каждый член этого
ряда больше соответствующего члена
гармонического ряда), следовательно,
обобщенно гармонический ряд расходится
при s
< 1.
Осталось
доказать сходимость ряда
при s
> 1.
Запишем
разность 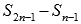 :
:
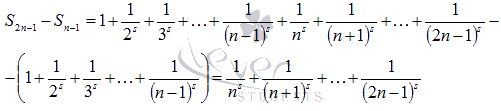 Очевидно,
что
Очевидно,
что  ,
тогда
,
тогда
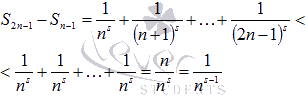 Распишем
полученное неравенство для n
= 2, 4, 8, 16, …
Распишем
полученное неравенство для n
= 2, 4, 8, 16, …
 Используя
эти результаты, с исходным числовым
рядом можно провести следующие
действия:
Используя
эти результаты, с исходным числовым
рядом можно провести следующие
действия:
 Выражение
Выражение  представляет
собой сумму геометрической прогрессии,
знаменатель которой равен
представляет
собой сумму геометрической прогрессии,
знаменатель которой равен  .
Так как мы рассматриваем случай при s
> 1,
то
.
Так как мы рассматриваем случай при s
> 1,
то 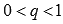 .
Поэтому
.
Поэтому 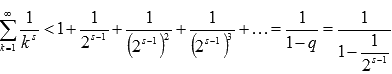 .
Таким образом, последовательность
частичных сумм обобщенно гармонического
ряда при s
> 1 является
возрастающей и в тоже время ограниченной
сверху значением
.
Таким образом, последовательность
частичных сумм обобщенно гармонического
ряда при s
> 1 является
возрастающей и в тоже время ограниченной
сверху значением 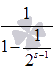 ,
следовательно, она имеет предел, что
указывает на сходимость ряда
.
Доказательство завершено.
,
следовательно, она имеет предел, что
указывает на сходимость ряда
.
Доказательство завершено.
Числовой
ряд
называется знакоположительным,
если все его члены положительны, то
есть, ![]() .
Числовой
ряд
.
Числовой
ряд ![]() называется знакочередующимся,
если знаки его соседних членов различны.
Знакочередующийся числовой ряд можно
записать в виде
называется знакочередующимся,
если знаки его соседних членов различны.
Знакочередующийся числовой ряд можно
записать в виде ![]() или
или ![]() ,
где
.
Числовой
ряд
называется знакопеременным,
если он содержит бесконечное множество
как положительных, так и отрицательных
членов.
Знакочередующийся числовой
ряд является частным случаем
знакопеременного ряда.
Ряды
,
где
.
Числовой
ряд
называется знакопеременным,
если он содержит бесконечное множество
как положительных, так и отрицательных
членов.
Знакочередующийся числовой
ряд является частным случаем
знакопеременного ряда.
Ряды
 являются
знакоположительным, знакочередующимся
и знакопеременным соответственно.
Для
знакопеременного ряда существует
понятие абсолютной и условной
сходимости.
Знакопеременный
ряд
называется абсолютно
сходящимся,
если сходится ряд из абсолютных величин
его членов, то есть, сходится
знакоположительный числовой ряд
являются
знакоположительным, знакочередующимся
и знакопеременным соответственно.
Для
знакопеременного ряда существует
понятие абсолютной и условной
сходимости.
Знакопеременный
ряд
называется абсолютно
сходящимся,
если сходится ряд из абсолютных величин
его членов, то есть, сходится
знакоположительный числовой ряд ![]() .
К
примеру, числовые ряды
.
К
примеру, числовые ряды ![]() и
и ![]() абсолютно
сходятся, так как сходится ряд
абсолютно
сходятся, так как сходится ряд ![]() ,
являющийся суммой бесконечно убывающей
геометрической прогрессии.
Знакопеременный
ряд
называется условно
сходящимся,
если ряд
расходится,
а ряд
сходится.
В
качестве примера условно сходящегося
числового ряда можно привести ряд
,
являющийся суммой бесконечно убывающей
геометрической прогрессии.
Знакопеременный
ряд
называется условно
сходящимся,
если ряд
расходится,
а ряд
сходится.
В
качестве примера условно сходящегося
числового ряда можно привести ряд  .
Числовой ряд
.
Числовой ряд 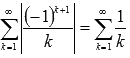 ,
составленный из абсолютных величин
членов исходного ряда, расходящийся,
так как является гармоническим. В то же
время, исходный ряд является сходящимся,
что легко устанавливается с помощью признака
Лейбница.
Таким образом, числовой знакочередующийся
ряд
условно
сходящийся.
К
началу страницы
,
составленный из абсолютных величин
членов исходного ряда, расходящийся,
так как является гармоническим. В то же
время, исходный ряд является сходящимся,
что легко устанавливается с помощью признака
Лейбница.
Таким образом, числовой знакочередующийся
ряд
условно
сходящийся.
К
началу страницы
Свойства сходящихся числовых рядов.
Если сходится числовой ряд , то сходящимся будет и ряд
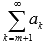 .
Другими словами, сходящимся будет и
ряд без первых m членов.
Если к сходящемуся числовому
ряду
добавить
несколько членов (от первого до m-ого),
то полученный ряд также будет сходящимся.
.
Другими словами, сходящимся будет и
ряд без первых m членов.
Если к сходящемуся числовому
ряду
добавить
несколько членов (от первого до m-ого),
то полученный ряд также будет сходящимся.
Если сходится числовой ряд и его сумма равна S, то сходящимся будет и ряд
 ,
причем
,
причем 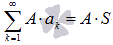 ,
где A –
произвольная постоянная.
,
где A –
произвольная постоянная.
Если сходятся числовые ряды и , их суммы равны A и B соответственно, то сходящимися будут ряды
 и
и  ,
причем их суммы будут равны A
+ B и A
- B соответственно.
,
причем их суммы будут равны A
+ B и A
- B соответственно.
Пример.
Докажите
сходимость числового ряда ![]() .
Решение.
Запишем
ряд в другом виде
.
Решение.
Запишем
ряд в другом виде  .
Числовой ряд
.
Числовой ряд ![]() сходится,
так как обобщенно гармонический
ряд
является
сходящимся при s
> 1,
а в силу второго свойства сходящихся
числовых рядов будет сходится и ряд с
числовым коэффициентом
сходится,
так как обобщенно гармонический
ряд
является
сходящимся при s
> 1,
а в силу второго свойства сходящихся
числовых рядов будет сходится и ряд с
числовым коэффициентом  .
Пример.
Сходится
ли числовой ряд
.
Пример.
Сходится
ли числовой ряд  .
Решение.
Преобразуем
исходный ряд:
.
Решение.
Преобразуем
исходный ряд: 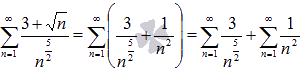 .
Таким образом, мы получили сумму двух
числовых рядов
.
Таким образом, мы получили сумму двух
числовых рядов ![]() и
и ![]() ,
причем каждый из них сходится (смотрите
предыдущий пример). Следовательно, в
силу третьего свойства сходящихся
числовых рядов, сходится и исходный
ряд.
,
причем каждый из них сходится (смотрите
предыдущий пример). Следовательно, в
силу третьего свойства сходящихся
числовых рядов, сходится и исходный
ряд.
42 Ряд Дирихле
Ряды Дирихле.
Рядами Дирихле называются функциональные ряды вида (1/anx), где числа an неограниченно возрастают; примером ряда Дирихле может служить дзета-функция Римана
![]()
Ряды Дирихле часто используются в теории чисел.
44 Знакопеременные ряды. Достаточный признак сходимости.
Определение 5. Числовые ряды, содержащие как положительные, так и отрицательные члены, называются знакопеременными рядами.
Ряды, все члены которых отрицательные числа, не представляют нового по сравнению со знакоположительными рядами, так как они получаются умножением знакоположительных рядов на –1.
Изучение знакопеременных рядов начнём с частного случая – знакочередующихся рядов.
Определение 6. Числовой ряд вида u1-u2+u3-u4+…+ +(-1)n-1.un+…, где un – модуль члена ряда, называется знакочередующимся числовым рядом.
Теорема 9. (Признак Лейбница)
Если для знакочередующегося числового ряда
![]() (19)
(19)
Выполняются два условия:
Члены ряда убывают по модулю u1>u2>…>un>…,
![]()
то ряд (19) сходится, причём его сумма положительна и не превосходит первого члена ряда.
Доказательство. Рассмотрим частичную сумму чётного числа членов ряда S2n=(u1-u2)+(u3-u4)+…+(u2n-1-u2n).
По условию u1>u2>…>u2n-1>u2n, то есть все разности в скобках положительны, следовательно, S2n возрастает с возрастанием n и S2n>0 при любом n.
С
другой
стороны S2n=u1-[(u2-u3)+(u4-u5)+…+(u2n-2-u2n-1)+u2n]. Выражение
в квадратных скобках положительно
и S2n>0,
поэтому S2n<u1 для
любого n.
Таким образом, последовательность
частичных сумм S2n возрастает
и ограничена, следовательно, существует
конечный ![]() S2n=S.
При этом 0<S≤u1.
S2n=S.
При этом 0<S≤u1.
Рассмотрим теперь частичную сумму нечётного числа членов ряда S2n+1=S2n+u2n+1. Перейдём в последнем равенстве к пределу при n→∞: S2n+1= S2n+ u2n+1=S+0=S. Таким образом, частичные суммы как чётного, так и нечётного числа членов ряда имеют один и тот же предел S, поэтому Sn=S, то есть данный ряд сходится. Теорема доказана.
Пример.
Исследовать
на сходимость ряд ![]()
Применим признак Лейбница.
un=![]() >un+1=
>un+1=![]()
un=
![]()
Оба условия признака Лейбница выполняются, следовательно, ряд сходится.
Замечания.
1. Теорема Лейбница справедлива и если условие un>un+1 выполняется, начиная с некоторого номера N.
2.
Условие un>un+1 не
является необходимым. Ряд может сходиться,
если оно не выполняется. Например,
ряд ![]()
![]() сходится,
как разность двух сходящихся рядов
сходится,
как разность двух сходящихся рядов ![]() хотя
условие un>un+1 не
выполняется.
хотя
условие un>un+1 не
выполняется.
Определение 8. Если знакопеременный ряд сходится, а ряд, составленный из абсолютных величин членов этого ряда, расходится, то говорят, что знакопеременный ряд сходится условно.
Определение 9. Если сходится и сам знакопеременный ряд и ряд, составленный из абсолютных величин его членов, то говорят, что знакопеременный ряд сходится абсолютно.
Пример.
Установить
характер сходимости ряда ![]()
Очевидно,
что данный ряд сходится по признаку
Лейбница. Действительно: ![]() и un=
и un=![]()
Ряд,
составленный из абсолютных величин
членов данного ряда ![]() является
расходящимся гармоническим рядом.
Поэтому данный ряд сходится условно.
является
расходящимся гармоническим рядом.
Поэтому данный ряд сходится условно.
Теорема 10. (Достаточный признак сходимости знакопеременного ряда или признак абсолютной сходимости)
Пусть
u1+u2+…+un+…=![]() (20)
(20)
знакопеременный ряд и пусть сходится ряд, составленный из абсолютных величин его членов
│u1│+│ u2│+…+│ un │+…=![]() │ un │. (21)
│ un │. (21)
Тогда ряд (20) тоже сходится.
Доказательство. Рассмотрим вспомогательный ряд
(u1+│u1│)+(u2+│u2│)+…+(un+│un│)+…= ![]() (un+│un│). (22)
(un+│un│). (22)
Очевидно, 0≤ un+│un│≤2│un│ при всех n=1, 2, … . Ряд (21) сходится по условию, поэтому сходится ряд 2│un│, тогда по признаку сравнения сходится ряд (22). Ряд (20) представляет собой разность двух сходящихся рядов (22) и (21), поэтому он тоже сходится. Теорема доказана.
Замечание.
Обратное утверждение неверно. Если данный ряд сходится, то ряд, составленный из абсолютных величин его членов, может и расходиться.
Например,
ряд
![]() сходится
по признаку Лейбница, а ряд
сходится
по признаку Лейбница, а ряд
![]() расходится
(это гармонический ряд).
расходится
(это гармонический ряд).
Остаток ряда и его оценка
Рассмотрим сходящийся числовой ряд
![]() (23)
(23)
Вычисление
суммы ряда S=![]() обычно
технически очень сложно. Поэтому в
качестве S берут S≈Sn.
Точность этого равенства возрастает с
увеличением n.
обычно
технически очень сложно. Поэтому в
качестве S берут S≈Sn.
Точность этого равенства возрастает с
увеличением n.
Определение 7. Если числовой ряд сходится, то разность Rn=S-Sn называется n-м остатком ряда.
Таким образом, Rn представляет собой сходящийся числовой ряд:
Rn= un+1+un+2+… .
Заметим, что Rn= ( S-Sn)=S-S=0.
Абсолютная погрешность при замене суммы ряда S его частичной суммой Sn равна |Rn|=|S-Sn|. Таким образом, если требуется найти сумму ряда с точностью до E>0, то надо взять сумму такого числа n первых членов ряда, чтобы выполнялось условие |Rn|<E. Однако в общем случае находить точно Rn не удаётся.
Теорема 11. (Об оценке остатка знакочередующегося числового ряда)
Если знакочередующийся числовой ряд сходится по признаку Лейбница, то его n-й остаток по абсолютной величине не превосходит модуля (n+1)-го члена ряда.
Доказательство. Пусть ряд u1-u2+u3-u4+…+(-1)n-1.un+… сходится по признаку Лейбница. Тогда n-й остаток ряда Rn=±(un+1-un+2+un+3-…) сам является суммой знакочередующегося числового ряда и по теореме Лейбница |Rn|≤|un+1|. Теорема доказана.
Пример.
Вычислить
с точностью до 0,01 сумму ряда ![]()
Очевидно,
ряд сходится по признаку
Лейбница. u1=![]() =1; u2=
=1; u2=![]() ≈
≈0,166; u3=
≈
≈0,166; u3=![]() ≈0,008<0,01.
Поэтому S≈1-0,166≈0,84.
≈0,008<0,01.
Поэтому S≈1-0,166≈0,84.
46 Понятие функционального ряда. Степенной ряд. Теорема Абеля.
О:
Функциональный ряд (ф.р.) представляет
собой ряд![]() ,
его члены — это функции от
,
его члены — это функции от![]()
Числовым
функциональный ряд можно назвать в том
случае, когда![]() является
фиксированным. Область сходимости ф.р.
есть множество
является
фиксированным. Область сходимости ф.р.
есть множество![]() значений
значений![]() ,
для которых он сходится.
,
для которых он сходится.
В области сходимости ф.р. .
Пример:
функциональный ряд![]() .
Определить область сходимости.
.
Определить область сходимости.
Поскольку его члены являются положительными, то для выявления области сходимости применим признак Даламбера:

если![]() то
ряд сходится.
то
ряд сходится.
Существенный частный случай ф.р. — степенный ряд.
О: Степенный ряд (с.р.) есть ф.р., который имеет следующий вид
(30.1)
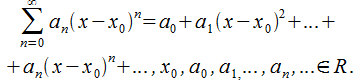
Если![]() ,
то ряд по степеням
можно
записать так:
,
то ряд по степеням
можно
записать так:
(30.2)
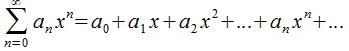
Для определения области сходимости с.р., представим доказательство теоремы Абеля.
Т.
(Абеля): В случае, когда степенной ряд
(30.2) сходится при![]() можно
заключить, что он абсолютно сходится
можно
заключить, что он абсолютно сходится![]() При
расходимости ряда (30.2) в т.
При
расходимости ряда (30.2) в т.![]() он
расходится
он
расходится![]() .
.
Предположим,
что ряд сходится,
соответственно
сходится,
соответственно![]()
Учитывая то, что функция, обладающая пределом, является ограниченной, можно обозначить
![]()
Представим ряд (30.2) в следующем виде
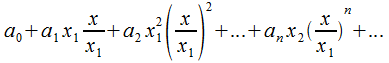 .
.
Для ряда, составленного из абсолютных величин его членов
(30.3)
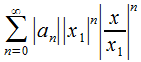
запишем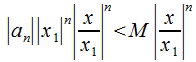 ,
при этом геометрическая прогрессия
,
при этом геометрическая прогрессия сходится
при
сходится
при Получается,
что, если
Получается,
что, если![]() в
соответствии с первым признаком сравнения
ряд (30.3) сходится, то по признаку абсолютной
сходимости ряд (30.2) сходится абсолютно.
в
соответствии с первым признаком сравнения
ряд (30.3) сходится, то по признаку абсолютной
сходимости ряд (30.2) сходится абсолютно.
Далее предположим, что при ряд (30.2) расходится. Допустим, что смысл теремы противоположен:
![]() ,
,
при
нем ряд (30.2) сходится. Однако в соответствии
с представленным ранее доказательством
ряд (30.2) предполагает сходимость в т.![]() .
Данное противоречие доказывает теорему.
.
Данное противоречие доказывает теорему.
48 Применение рядов к интегрированию функций.
