Погрешность интерполирования

Поставим вопрос о том, насколько хорошо интерполяционный полином   приближает функцию   на отрезке [a,b]. Рассмотри м остаточный член: , x ∈ [a, b]. По определению интерполяционного полинома    поэтому речь идет об оценке   при значениях  . Пусть   имеет непрерывную (n+1) производную на отрезке [a, b]. Тогда погрешность определяется формулой: , где  , - точка из [a, b]. Так как точка   наизвестна, то эта формула позволяет только оценить погрешность: где  Из вида множетеля   следует, что оценка имеет смысл только при  . Если это не так, то при интерполяции используются полиномы низких степеней (n = 1,2). 

55. Сплайн-интерполяция.

Точность полиномиальной аппроксимации катастрофически падает при увеличении степени аппроксимирующих полиномов. От этого недостатка можно избавиться, используя для аппроксимации отрезки полиномов невысокой степени, применяемые для представления части узловых точек. Самым известным методом такой аппроксимации является сплайн-аппроксимация на основе применения отрезков кубических полиномов. При этом аппарат сплайн- аппроксимации позволяет получить полиномы, которые дают в узловых точках непрерывность не только представляемой ими функции, но и ее первых и даже вторых производных.

Наглядно сплайн-функцию можно представить в виде гибкой стальной линейки, закрепленной в узловых точках и плавно изгибающейся. Благодаря указанным свойствам сплайнов они неплохо описывают функции, представленные как небольшим числом узловых точек (благодаря плавности сплайн- кривых), так и функции, представляемые очень большим числом узловых точек (поскольку порядок полиномов от этого числа уже не зависит). Недостатком сплайн- аппроксимации является отсутствие общего выражения для всей кривой. Фактически приходится использовать набор сплайн- функций для различных интервалов между узловыми точками.

Для получения сплайн- интерполяций используется Maple-функция spline (X, Y, var, d).

Здесь X и Y — одномерные векторы одинакового размера, несущие значения координат узловых точек исходной функции (причем в произвольном порядке), var — имя переменной, относительно которой вычисляется сплайн-функция, наконец, необязательный параметр d задает вид сплайна. Он может иметь следующие значения: 1inear — линейная функция, или полином первого порядка, quadratic — квадратичная функция, или полином второго порядка, cubic — полином третьего порядка, quartiс — полином четвертого порядка. Если параметр d опущен, то сплайн-функция будет строиться на основе полиномов третьего порядка (кубические сплайны).

Технику сплайновой аппроксимации наглядно поясняет рис. 9.6. На нем представлено задание векторов узловых точек X и Y и четырех сплайновых функций, по которым построены их графики. Для одной из функций (с линейной интерполяцией между узлами) показан вид сплайновой функции.

Кубическим интерполяционным сплайном, соответствующим данной функции f(x) и данным узлам x_i, называется функцияS(x), удовлетворяющая следующим условиям:

1. на каждом сегменте [x_{i -} 1, x_i], i = 1, 2, ..., N функция S(x) является полиномом третьей степени,

2. функция S(x), а также ее первая и вторая производные непрерывны на отрезке [a, b],

3. S(x_i) = f(x_i), i = 0, 1, ..., N.

4. На каждом из отрезков [x_{i -} 1, x_i], i = 1, 2, ..., N будем искать функцию S(x) = S_i(x) в виде полинома третьей степени:

   Si(x) = ai + bi(x - xi - 1) + ci(x - xi - 1)^2 + di(x - xi - 1)^3, xi - 1 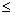 x   xi,

   (23)

5. где a_i, b_i, c_i, d_i - коэффициенты, подлежащие определению на всех n элементарных отрезках. Чтобы система алгебраических уравнений имела решение, нужно, чтобы число уравнений точно равнялось числу неизвестных. Поэтому мы должны получить 4n уравнения.

6. Первые 2n уравнения мы получим из условия, что график функции S(x) должен проходить через заданные точки, т. е.S_i(x_{i -} 1) = y_{i -} 1, S_i(x_i) = y_i. Эти условия можно записать в виде:

   Si(xi - 1) = ai = yi - 1, Si(xi) = ai + bihi + cih  + dih  = yi,

   (24)   (25)

7. где

   hi = xi - xi - 1, i = 1, 2, ..., n.

8. Следующие 2n - 2 уравнения вытекают из условия непрерывности первых и вторых производных в узлах интерполяции, т. е. условия гладкости кривой во всех точках.

   S' i + 1(xi) = S' i(xi), i = 1, ..., n - 1, S' ' i + 1(xi) = S' ' i(xi), i = 1, ..., n - 1, S' i (x) = bi + 2 ci (x - xi - 1) + 3 di (x - xi - 1) 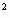, S' i + 1 (x) = bi + 1 + 2 ci + 1 (x - xi) + 3 di + 1 (x - xi) .

9. Приравнивая в каждом внутреннем узле x = x_i значения этих производных, вычисленные в левом и правом от узла интервалах, получаем (с учетом h_i = x_i - x_{i -} 1):

   bi + 1 = bi + 2 hi ci + 3h di, i = 1, ..., n - 1, S' ' i(x) = 2 ci + 6 di (x - xi - 1), S' ' i + 1(x) = 2 ci + 1 + 6 di + 1 (x - xi),

   (26)

10. если x = x_i

    ci + 1 = ci + 3 hi di, i = 1,2, ..., n - 1.

    (27)

11. На данном этапе мы имеем 4n неизвестных и 4n - 2 уравнений. Следовательно, необходимо найти еще два уравнения.

12. При свободном закреплении концов можно приравнять к нулю кривизну линии в этих точках. Из условий нулевой кривизны на концах следуют равенства нулю вторых производных в этих точках:

    S1' ' (x0) = 0 и Sn' ' (xn) = 0, ci = 0 и 2 cn + 6 dn hn = 0.

    (28)

13. Уравнения (24) - (28) составляют систему линейных алгебраических уравнений для определения 4n коэффициентов: a_i , b_i , c_i, d_i (i = 1, 2, . . ., n).

14. Эту систему можно привести к более удобному виду. Из условия(24) сразу можно найти все коэффициенты a_i.

15. Далее из (27) и (28) получим:

    di = ,i = 1, 2, ..., n - 1, dn = - cn/(3hn)

    (29)

16. Подставляя (24) и (28) в (25), получим:

bi = - (ci + 1 + 2ci) , i = 1,2, ..., n - 1, bn = - (hn cn)

(30)

Учитывая выражения (29) и (30), исключаем из уравнения (27) коэффициенты b_i и d_i . Окончательно получим следующую систему уравнений только для коэффициентов с_i:

c₁ = 0 и c_{n +} 1 = 0:

hi - 1 ci - 1 + 2 (hi - 1 + hi) ci + hi ci + 1 = 3 ( - ), i = 2, 3, ..., n.

(31)

По найденным коэффициентам с_i легко вычислить d_i ,b_i.

Матрица этой системы трехдиагональная. Т. е. ненулевые элементы находятся лишь на главной и двух соседних с ней диагоналях, расположенных сверху и снизу.