Циркуляция вектора магнитной индукции

Возьмём контур, охватывающий прямой ток, и вычислим для него циркуляцию вектора , т.е.

Р ассмотрим вначале случай, когда контур лежит в плоскости, перпендикулярной току (ток направлен за чертёж). В каждой точке поля вектор направлен по касательной к окружности, проходящей через эту точку (линии индукции прямого тока окружности). Воспользуемся свойством скалярного произведения векторов , где dl_B – проекция вектора dl на направление вектора индукции B.

R – расстояние от тока до вектора dl. Мы знаем, что для прямого тока индукция равна.

Тогда получим.

Отсюда найдём циркуляцию вектора магнитной индукции.

При обходе контура угол  изменяется от нуля до 2, при этом радиальная прямая поворачивается в одном направлении. Для напряжённости магнитного поля выражение для циркуляции будет иметь вид.

П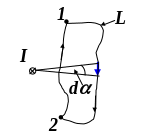 о-другому обстоит дело, если ток не охватывается контуром. В этом случае при обходе контура радиальная прямая поворачивается сначала в одном направлении (1 2),

а потом в другом (2  1).

В этом случае

Итак, в общем случае (1)

I – ток, охватываемый контуром.

Эта формула справедлива и для тока произвольной формы, и для контура произвольной формы.

Если контур охватывает несколько токов, то выражение (1) примет вид.

(2)

Или для напряжённости магнитного поля.

Если ток распределен по объему, где расположен контур , то этот ток можно представить, как . Интеграл берется по произвольной поверхности , "натянутой" на контур . Плотность тока под интегралом – это плотность в точке, где расположена площадка . Вектор образует с направлением обхода по контуру правовинтовую систему.

Т аким образом, уравнение для циркуляции в общем случае будет выглядеть так:

Вычисляя сумму токов, положительными следует считать те токи, направление которых связано с направлением обхода контура правилом правого винта.

Итак, циркуляция вектора магнитной индукции отлична от нуля, если контур охватывает ток.

(Сравните с циркуляцией вектора электрического поля E, где )

Такие поля называются вихревыми (или соленоидными). Поэтому магнитному полю нельзя приписать потенциал. Этот потенциал не был бы однозначным – после каждого обхода по контуру он бы получал приращение ₀I.

Как мы знаем, линии напряжённости электростатического поля начинаются и заканчиваются на зарядах. Опыт показывает, что линии магнитной индукции всегда замкнуты. Поэтому магнитных зарядов в природе не существует.

Английский физик-теоретик Поль Дирак в 1931 году высказал предположение, что в природе должны существовать магнитные заряды (названные монополями Дирака). Поиски этих зарядов пока не дали никаких результатов, так что вопрос о существовании монополей Дирака остаётся открытым.

Следствием того, что линии магнитной индукции замкнуты, является то, что поток вектора B через замкнутую поверхность должен быть равен нулю. Таким образом, для любого магнитного поля и произвольной замкнутой поверхности S имеет место условие.

Эта формула выражает теорему Гаусса для вектора B. Поток вектора магнитной индукции через любую замкнутую поверхность равен нулю.

Заменим в последнем выражении поверхностный интеграл объёмным и получим.

Условие, к которому мы пришли, должно выполняться для любого произвольного объёма V. Это возможно лишь в том случае, если подынтегральная функция в каждой точке поля равна нулю. Таким образом, магнитное поле обладает тем свойством, что его дивергенция всюду равна нулю.

П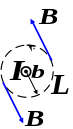 рименение теоремы о циркуляции вектора в ряде случаев значительно упрощает расчет поля , особенно при решении симметричных задач. Особенно просто рассчитывается поле , если вычисление циркуляции можно свести к произведению или проекции на длину контура или его часть.

Пример. Вычислим магнитное поле прямого тока (решение этой задачи с использованием закона Био–Савара–Лапласа рассмотрено нами в начале семестра). Пусть ток направлен перпендикулярно плоскости рисунка, к нам. Линии вектора имеют вид окружностей с центром на оси тока. Во всех точках на расстоянии от центра модуль вектора одинаков. Выберем круглый контур вне проводника на расстоянии от оси проводника. Применим теорему о циркуляции вектора для выбранного круглого контура:

В итоге получили выражение , откуда , что совпадает с выражением, полученным в первой лекции этого семестра.

Теорему о циркуляции вектора магнитной индукции можно использовать для расчёта более сложных источников поля.

Рассмотрим дифференциальную форму представления циркуляции вектора магнитной индукции.

Если токи текут во всём пространстве, где расположен контур, алгебраическую сумму токов, охватываемых контуром, можно представить в виде.

(3)

Интеграл берётся по произвольной поверхности S, натянутой на контур. Вектор j есть плотность тока в той точке, где расположена площадка dS; n – положительная нормаль к этой площадке (т.е. нормаль, образующая с направлением обхода по контуру при вычислении циркуляции правовинтовую систему). Заменив в (2) сумму токов выражением (3), получим.

Преобразуем левую часть по теореме Стокса. Вспомним её смысл. Циркуляция вектора A по произвольному контуру B равна потоку вектора rotA через произвольную поверхность S, ограниченную данным контуром. Придём к равенству.

 – оператор набла. Если он действует на скаляр, то это градиент, а если на вектор, то это дивергенция.

Полученное равенство должно выполняться при произвольном выборе поверхности S, по которой берётся интеграл. Это возможно лишь в том случае, если подынтегральные функции имеют в каждой точке одинаковые значения. Таким образом, мы приходим к выводу, что ротор вектора магнитной индукции пропорционален вектору плотности тока в данной точке.

(4)

Напомним о роторе. Воспользовавшись записью векторного произведения с помощью определителя.

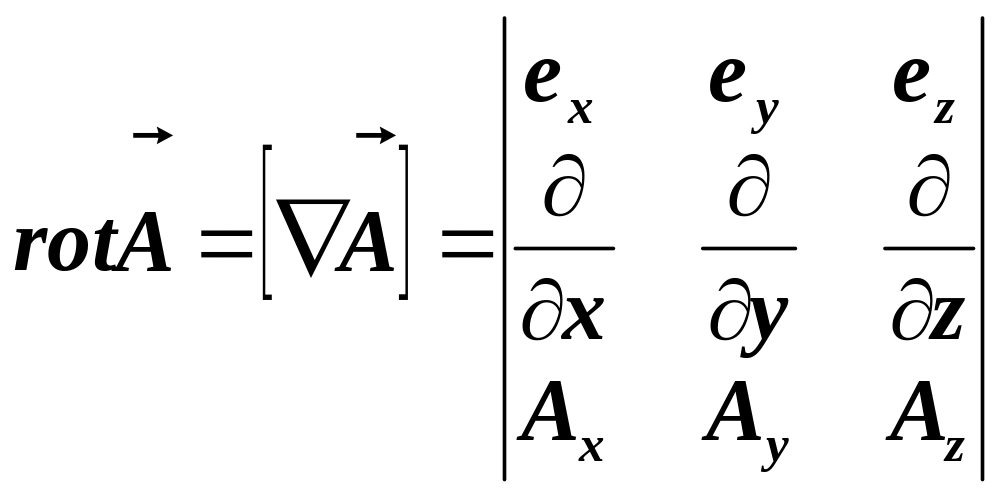
Отметим, что выражения (2) и (4) справедливы только для поля в вакууме в отсутствии меняющихся во времени электрических полей.