
Гл. 7. Системы линейных алгебраических уравнений.
§1. Основные понятия.
 (*)
(*)

![]() -
есть общий вид системы
-
есть общий вид системы
![]() линейных уравнений с
линейных уравнений с
![]() неизвестными
неизвестными
![]() .
.
Число
![]() ,
,
![]() ,
,
![]() ,
называются коэффициентами, а
,
называются коэффициентами, а
![]() ,
,
![]() -
свободными членами.
-
свободными членами.
Линейную систему можно записать в матричной форме.
Матрицу,
![]() составленную из коэффициентов, при
переменных, называют основной матрицей
системы:
составленную из коэффициентов, при
переменных, называют основной матрицей
системы:

Матрица,
![]() полученная из основной матрицы
присоединением столбца свободных членов
называется расширенной матрицей системы.
полученная из основной матрицы
присоединением столбца свободных членов
называется расширенной матрицей системы.

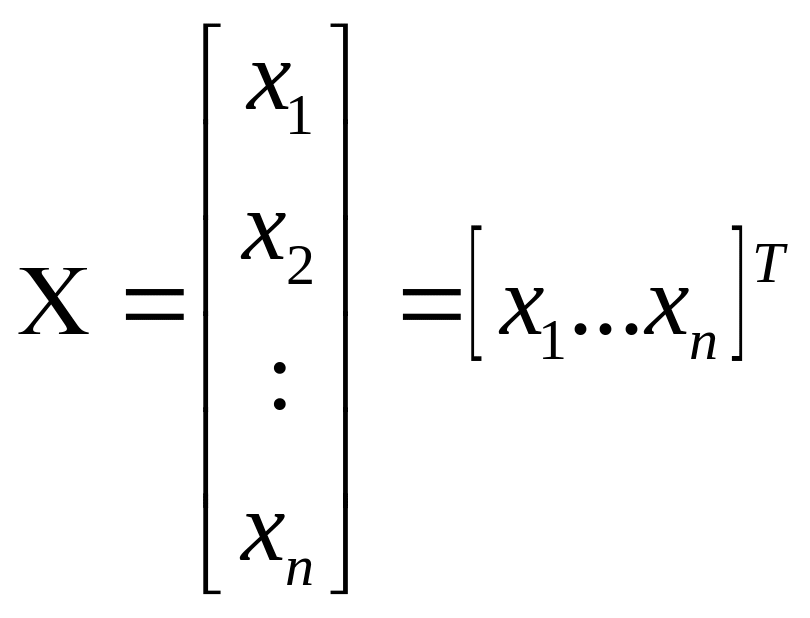 -
матрица столбец неизвестных.
-
матрица столбец неизвестных.
 -
матрица – столбец свободных членов.
-
матрица – столбец свободных членов.
Тогда система запишется в форме:
![]()
![]() -
умножение
возможно.
-
умножение
возможно.

![]()
Производя умножение, получаем уравнения системы:
![]() ,
где
-
номер уравнения.
,
где
-
номер уравнения.
Матрица
столбец
 называется решением
,
если при подстановке матрицы
называется решением
,
если при подстановке матрицы
![]() вместо
вместо
![]() матричное уравнение
становиться верным равенством.
матричное уравнение
становиться верным равенством.
Если система имеет хотя бы одно решение, то называется совместной, если не имеет ни одного решения, то не совместной.
Совместная система называется определенной, если имеет единственное решение, и не определенной, если имеет более одного решения.
Решить систему-это значит выяснить совместна она или нет, и в случае совместности найти все ее решения.
П римеры:
римеры:
1.
![]() .
.
![]() .
.
![]() -
решение системы единственно, она
совместна и определена.
-
решение системы единственно, она
совместна и определена.
 .
.
Система состоит из одного уравнения, она совместна, не определена.
Пусть
![]() ,
,
![]() -
произвольные числа, тогда решение
запишется
-
произвольные числа, тогда решение
запишется

 ;
;
 -
решений
бесконечное множество.
-
решений
бесконечное множество.
 .
Система не совместна (нет ни одного
решения).
.
Система не совместна (нет ни одного
решения).
Системы называются равносильными, если любое решение одной из них является решением другой и наоборот. Любое две не совместные системы считаются (эквивалентными) равносильными.
К элементарным преобразованиям системы относятся следующие:
10.
Умножение уравнения системы на некоторое
число,
![]() .
.
20. Сложение одного уравнения системы с другим умноженным на некоторое число.
30. Перестановка уравнений системы.
При элементарных преобразования система переходит в равносильную (эквивалентную) систему. Элементарные преобразования можно выполнить не над самой системой, а над ее решенной матрицей .
§ 2. Крамеровские системы.
Рассмотрим систему линейных уравнений, в которой число неизвестных равно числу уравнений. Такие системы называются Крамеровскими.

![]()
Определителем
системы (1) называется определитель
![]() основной матрицы системы, которая в
данном случае квадратного порядка
.
основной матрицы системы, которая в
данном случае квадратного порядка
.
Обозначим
через
![]() определитель, полученный заменой в
определителе
столбца коэффициентов при неизвестном
определитель, полученный заменой в
определителе
столбца коэффициентов при неизвестном
![]() столбцом свободных членов системы.
столбцом свободных членов системы.
 ,
,
 .
(2)
.
(2)
где
![]() .
.
Теорема: “Если определитель системы (1) отличен от 0, то система совместна и определена, то есть имеет единственное решение вида:
![]() ,
,
![]() ,
…
,
…
![]() ,
где
и
,
где
и
![]()
![]() определены формулами (2).
определены формулами (2).
Доказательство:
Систему
(1) запишем в матричной
форме
![]() .
.
По
условию теоремы
![]() ,
поэтому для основной матрицы системы
существует обратная матрица
,
поэтому для основной матрицы системы
существует обратная матрица
![]() ,
определяемая формулой:
,
определяемая формулой:
 ,
,
![]() -
алгоритмические
дополнения матрицы
-
алгоритмические
дополнения матрицы
![]() .
.
Умножив обе части матричного уравнения на , получим:
![]() .
.
![]() .
(3)
.
(3)
![]() .
.
Равенство (3) запишем матрицами:
 или
или

![]() .
.
Отсюда,
![]() ,
.
(4)
,
.
(4)
Рассмотрим
разложение определителя
по
![]() столбцу.
столбцу.
 .
(5)
.
(5)
Таким образом в правой части равенства (4), в скобках, записано выражение равное определителю . Отсюда:
![]() ,
.
(6)
,
.
(6)
Доказанная теорема называется теоремой Крамера, а формула (6) – формулами Крамера.
Пример: Решить систему
 .
.
Число уравнений равно числу переменных – система Крамеровская.
 -
условие теоремы выполнено.
-
условие теоремы выполнено.

 .
.
 .
.
Система имеет единственное решение
![]() .
.
![]() .
.
![]() .
.
