25. Полярные и цилиндрические координаты

Полярные координаты  точки на плоскости, два числа, которые определяют положение этой точки относительно некоторой фиксированной точки О (полюс) и некоторого фиксированного луча ON (полярной оси), исходящего из полюса. Эти числа ρ (полярный радиус) и φ (полярный угол) равны соответственно расстоянию от О до Р и углу между ON и ОР. Угол φ называют иногда амплитудой, точки Р. Для взаимно однозначного соответствия между точками плоскости и парами П. к. изменение П. к. обычно ограничивают промежутками: 0 ≤ ρ ≤ + ∞; 0 ≤ φ < 2π (при этом полярный угол полюса остаётся неопределённым). Если же однозначности предпочитают непрерывность (чтобы при непрерывном движении точки её П. к. изменялись также непрерывно), то в качестве полярного угла берут величину φ₀ + kπ (k — произвольное число), где φ₀ есть угол NOP, а полярному радиусу приписывают знак + или —, смотря по тому, совпадает ли направление луча ОР с направлением, получающимся в результате поворота оси ON на угол, равный выбранному значению полярного угла, или же эти направления противоположны.

        

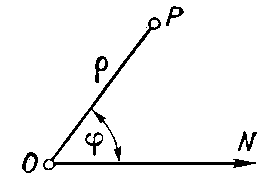
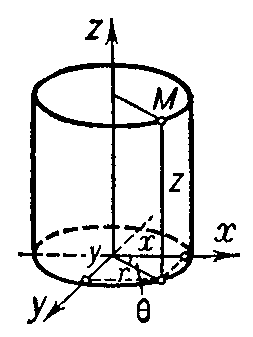
Цилиндрические координаты точки М, три числа r, θ, z, характеризующие положение точки в пространстве. Наименование Ц. к. связано с тем, что координатная поверхность r = const является цилиндром, образующие которого параллельны Oz. Ц. к. и прямоугольные координаты х, у, z точки М связаны соотношениями: х = rcosθ, у = rsinθ, z = z.

        

40. Неопределённые выражения в математике, выражения, предел которых не может быть найден путём непосредственного применения теорем о пределах. Типы Н. в.:

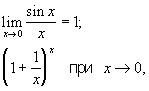
где e = 2,71828... — неперово число. Указанные типы Н. в. символически обозначают так:

30.Числовые последовательности и их свойства. Действия с числовыми последовательностями. Числовая последовательность — это последовательность элементов числового пространства. Числовые последовательности являются одним из основных объектов рассмотрения в математическом анализе. Пусть множество X — это либо множество вещественных чисел , либо множество комплексных чисел . Тогда последовательность элементов множества X называется числовой последовательностью. Суммой числовых последовательностей (x_n) и (y_n) называется числовая последовательность (z_n) такая, что z_n = x_n + y_n.

Разностью числовых последовательностей (x_n) и (y_n) называется числовая последовательность (z_n) такая, что z_n = x_n − y_n.

Произведением числовых последовательностей x_n и y_n называется числовая последовательность (z_n) такая, что .

Частным числовой последовательности x_n и числовой последовательности y_n, все элементы которой отличны от нуля, называется числовая последовательность . Если в последовательности y_n на позиции всё же имеется нулевой элемент, то результат деления на такую последовательность всё равно может быть определён, как последовательность 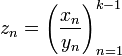. Свойства: Всякая последовательность является своей подпоследовательностью.

Для всякой подпоследовательности верно, что .

Подпоследовательность сходящейся последовательности сходится к тому же пределу, что и исходная последовательность.

Если все подпоследовательности некоторой исходной последовательности сходятся, то их пределы равны.

Любая подпоследовательность бесконечно большой последовательности также является бесконечно большой.

Из любой неограниченной числовой последовательности можно выделить бесконечно большую подпоследовательность, все элементы которой имеют определённый знак. Из любой числовой последовательности можно выделить либо сходящуюся подпоследовательность, либо бесконечно большую подпоследовательность, все элементы которой имеют определённый знак. Предел последовательности — это объект, к которому члены последовательности приближаются с ростом номера. Так в произвольном топологическом пространстве пределом последовательности называется элемент, в любой окрестности которого лежат все члены последовательности, начиная с некоторого. В частности для числовых последовательностей предел — это число, в любой окрестности которого лежат все члены последовательности начиная с некоторого.Частичный предел последовательности — это предел одной из её подпоследовательностей. У сходящихся числовых последовательностей он всегда совпадает с обычным пределом.Верхний предел последовательности — это наибольшая предельная точка этой последовательности.Нижний предел последовательности — это наименьшая предельная точка этой последовательности.

32. Свойства сходящихся последовательностей. Основные теоремы о пределах. Сходящаяся последовательность — это последовательность элементов множества X, имеющая предел в этом множестве.

Свойства : Всякая бесконечно малая последовательность является сходящейся. Её предел равен нулю. Удаление любого конечного числа элементов из бесконечной последовательности не влияет ни на сходимость, ни на предел этой последовательности.

Любая сходящаяся последовательность элементов хаусдорфова пространства имеет только один предел.

Любая сходящаяся последовательность ограничена. Однако не любая ограниченная последовательность сходится.

Последовательность сходится тогда и только тогда, когда она является ограниченной и при этом её верхний и нижний пределы совпадают.

Если последовательность (x_n) сходится, но не является бесконечно малой, то, начиная с некоторого номера, определена последовательность (1 / x_n), которая является ограниченной.

Сумма сходящихся последовательностей также является сходящейся последовательностью.

Разность сходящихся последовательностей также является сходящейся последовательностью.

Произведение сходящихся последовательностей также является сходящейся последовательностью.

Частное двух сходящихся последовательностей определено, начиная с некоторого элемента, если только вторая последовательность не является бесконечно малой. Если частное двух сходящихся последовательностей определено, то оно представляет собой сходящуюся последовательность.

Если сходящаяся последовательность ограничена снизу, то никакая из её нижних граней не превышает её предела.

Если сходящаяся последовательность ограничена сверху, то её предел не превышает ни одной из её верхних граней.

Если для любого номера члены одной сходящейся последовательности не превышают членов другой сходящейся последовательности, то и предел первой последовательности также не превышает предела второй.

Если все элементы некоторой последовательности, начиная с некоторого номера, лежат на отрезке между соответствующими элементами двух других сходящихся к одному и тому же пределу последовательностей, то и эта последовательность также сходится к такому же пределу.

Любую сходящуюся последовательность (x_n) можно представить в виде (x_n) = (a + α_n), где a — предел последовательности (x_n), а α_n — некоторая бесконечно малая последовательность.

Всякая сходящаяся последовательность является фундаментальной. При этом фундаментальная числовая последовательность всегда сходится (как и любая фундаментальная последовательность элементов полного пространства). Теоремы о пределах. 1. Предел суммы есть сумма пределов. 2. Предел произведения есть произведение пределов. 3. Предел частного есть частное пределов (если знаменатель не обращается в 0).4. Если u(x)  z(x)  v(x), и lim_{x a} u(x)=lim_{x a} v(x)=b, то lim_{x a} z(x)=b. ("Теорема о двух милиционерах").

Теорема 1. (о единственности предела функции). Функция не может иметь более одного предела .Следствие. Если две функции f(x) и g(x) равны в некоторой окрестности точки , за исключением, может быть, самой точки , то либо они имеют один и тот же предел при , либо обе не имеют предела в этой точке. Теорема 2. Если функции f(x) и  g(x) имеют пределы в точке , то:1) предел алгебраической суммы функций равен алгебраической сумме пределов слагаемых, т.е.

         (2)2) предел произведения функций равен произведению пределов сомножителей, т.е.

            (3)3)предел частного двух функций равен частному от деления предела делимого на предел делителя, если предел делителя не равен нулю, т.е.

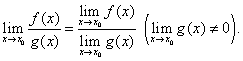           (4) Следствие 1. Предел постоянной равен самой постоянной, т.е.

Следствие 2. Постоянный множитель можно выносить за знак предела, т.е.

Теорема 3 (о пределе сложной функции). Если существует конечный предел

а функция f(u) непрерывна в точке , то

Другими словами, для непрерывных функций символы предела и функции можно поменять местами.

1.  Предел константы равен самой этой константе:

с = с.

2.  Постоянный множитель можно выносить за знак предела:

[ k •  f (х)] = k •   f (х).

3.  Предел суммы (разности) функций равен сумме (разности) пределов этих функций:

[ f (х) ± g (х)] =   f (х) ±  g (x).

4.  Предел произведения функций равен произведению пределов этих функций:

[ f (х) • g (х)] =   f (х) •   g (x).

5.  Предел отношения двух функций равен отношению пределов этих функций, если только предел делителя не равен нулю:

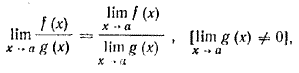
37. Бесконечно малые функции, свойства бесконечно малых. 2. Бесконечно большие величины, связь бесконечно больших с бесконечно малыми. Бесконечно малая величина Функция  называется бесконечно малой величиной при  или при , если ее предел равен нулю:

Свойства бесконечно малых величин 1)        Алгебраическая сумма конечного числа бесконечного малых величин есть величина бесконечно малая. 2)   Произведение бесконечно малой величины на ограниченную функцию (в т.ч. на постоянную, на другую бесконечно малую) есть величина бесконечно малая.3)   Частное от деления бесконечно малой величины на функцию, предел которой отличен от нуля, есть величина бесконечно малая. Бесконечно большие величины. Функция  называется бесконечно большой при , если ее предел равен бесконечности: Свойства бесконечно больших величин

1)      Произведение бесконечно большой величины на функцию, предел которой отличен от нуля, есть величина бесконечно большая.

2)       Сумма бесконечно большой величины и ограниченной функции есть величина бесконечно большая.

3)     Частное от деления бесконечно большой величины на функцию, имеющую предел, есть величина бесконечно большая. Связь между бесконечно малыми и бесконечно большими величинами Теорема. Если функция  есть бесконечно малая величина при  ( ), то функция  является бесконечно большой при  ( ). И, наоборот, если функция  бесконечно большая при  ( ), то функция  есть величина бесконечно малая при  ( ).

33. Функция вещественного аргумента. Элементарные функции. Функция вещ.аргумента Значение вещественного аргумента должно быть положительным. Значение комплексного аргумента должно отличаться от нуля. Результат имеет тот же тип, что и аргумент. Случайной функцией вещественного аргумента t называется функция X ( t), значения которой являются случайными величинами. Если аргумент t может принимать любые значения из некоторого ( конечного или бесконечного) интервала, то случайную функцию называют случайным процессом; если аргумент t может принимать только дискретные значения, то X ( t) называют случайной последовательностью. Элементарные функции: К элементарным функциям относятся основные элементарные функции и те, которые можно образовать из них с помощью конечного числа операций (сложения, вычитания, умножения и деления) и суперпозиций. Выделим классы функций, которые получены из элементарных: 1)Целая рациональная функция (или многочлен): y=a₀xⁿ+a₁x^n-1+...+a_n, где n - целое неотрицательное число (степень многочлена), a₀, a₁, ..., a_n - постоянные числа (коэффициенты). 2) Дробно-рациональная функция, которая является отношением двух целых рациональных функций. Целые рациональные и дробно-рациональные образуют класс рациональных функций. 3) Иррациональная функция - это та, которая строится с помощью суперпозиции рациональной функции и степенных функций с рациональными показателями. \\Рациональная и иррациональная функции образуют класс алгебраических функций. Алгебраическая функция - произвольная функция y=f(x), которая удовлетворяет уравнению: A₀(x)yⁿ+A₁(x)y^n-1+...+A_n-1(x)y+A_n(x)=0. Элементарные функции, которые не являются алгебраическими, называются трансцендентными

34. Предел и непрерывность функции. Классификация точек разрыва.

Предел функции- Число b – предел функции f(x) при x стремящемся к a, если для каждого положительного числа e можно указать такое положительной число d, что для всех x, отличных от a и удовлетворяющих неравенству |x-a|<d, имеет место неравенство |f(x)-b|<d. Если b есть предел функции f(x) при x стремящемся к a, то записывают это так: непрерывность функции Функция f(x) непрерывна в точке a, если Точка   называется точкой разрыва функции y = f(x), если она принадлежит области определения функции или её границе и не является точкой непрерывности. Классификация точек разрыва: если оба односторонних предела существуют и конечны, но хотя бы один из них отличен от значения функции в данной точке, то такую точку называют точкой разрыва первого рода; \\\\если хотя бы один из односторонних пределов не существует или не является конечной величиной, то такую точку называют точкой разрыва второго рода. \\\\Точка, в которой функция не определена, будет точкой разрыва функции лишь при условии, если функция определена, хотя бы с одной стороны вблизи этой точки.

35. Свойства непрерывных функций. Действия с непрерывными функциями.

Свойства непрерывных функций. Локальные

Функция, непрерывная в точке  , является ограниченной в некоторой окрестности этой точки.

Если функция   непрерывна в точке   и   (или  ), то   (или  ) для всех  , достаточно близких к  .

Если функции f и g непрерывны в точке a, то функции   и   тоже непрерывны в точке  .

Если функции f и g непрерывны в точке a и при этом  , то функция   тоже непрерывна в точке  .

Если функция f непрерывна в точке a и функция g непрерывна в точке  , то их композиция   непрерывна в точке a. Глобальные:

Функция, непрерывная на отрезке, равномерно непрерывна на нём.

Функция, непрерывная на отрезке (или любом другом компактном множестве), ограничена и достигает на нём свои максимальное и минимальное значения.

Областью значений функции f, непрерывной на отрезке  , является отрезок   где минимум и максимум берутся по отрезку  .

Если функция f непрерывна на отрезке   и   то существует точка   в которой  .

Если функция f непрерывна на отрезке   и число   удовлетворяет неравенству   или неравенству   то существует точка   в которой  .

Непрерывное отображение отрезка в вещественную прямую инъективно в том и только в том случае, когда данная функция на отрезке строго монотонна.

Монотонная функция на отрезке   непрерывна в том и только в том случае, когда область ее значений является отрезком с концами   и  .

Если функции f и g непрерывны на отрезке  , причем   и   то существует точка   в которой   Отсюда, в частности, следует, что любое непрерывное отображение отрезка в себя имеет хотя бы одну неподвижную точку. действия над непрерывными функциями Если точка  - предельная точка области определения функции f(x), то функция f(x) непрерывна в точке , если она определена в этой точке, имеет в этой точке предел, и значение этого предела совпадает со значением функции в точке .

36. Поведение функции на бесконечности. Поведение функции на бесконечности. . При исследовании поведения функции на бесконечности необходимо проверить, не имеет ли график функции наклонных асимптот при и . Для этого нужно вычислить следующие пределы: и . Если оба предела существуют, то – уравнение наклонной асимптоты при . Частный случай наклонной асимптоты при – горизонтальная асимптота. Аналогично ищется наклонная асимптота при .